推导如下:
由于方差是每个数据与均值离差平方和的均值:即对Σ(每个数据-均值)²再求一次均值👇
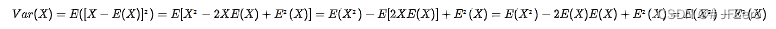
最终Var(X) = E(X²)-E²(X)
因此👇
Var(X-Y) = E(X-Y)²-E²(X-Y)
=E(X²-2XY+Y²)-[E(X)-E(Y)]²
=E[ X²-2XY+Y²-E²(X)+2E(X)E(Y)-E²(Y) ]
=E(X²)-2E(XY)+E(Y²)-E²(X)+2E(X)E(Y)-E²(Y)
=E(X²)-E²(X)+E(Y²)-E²(Y)-2[E(XY)-E(X)E(Y)]
其中 E(X²)-E²(X) 为 Var(X) ,E(Y²)-E²(Y)为Var(Y)
而 E(XY)-E(X)E(Y) 为X和Y的协方差Cov(X,Y)
为什么E(XY)-E(X)E(Y)是协方差?(推导如下)

最终可得:Var(X-Y) = Var(X)+Var(Y)-2*Cov(X,Y)
同理可证:Var(X+Y) = Var(X)+Var(Y)-2*Cov(X,Y)