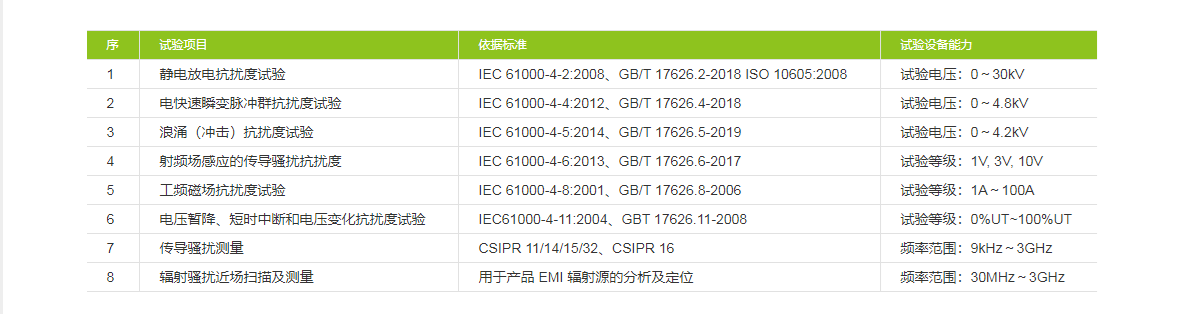
一、float基础：
Float类型占4个字节,也就是32bit,其中最高位是符号位,2~9位是指数位,后边的23bit是数值位.如下所示
大部分数据的二进制形式都可以用科学计数法表示,即1.m*2^n这种形式,只要知道m和n,就能确定一个数值
二、小数位如何转变为二进制：
下面我们具体计算一下0.6的小数表示过程
0.6 * 2 = 1.2 ——————- 1
0.2 * 2 = 0.4 ——————- 0
0.4 * 2 = 0.8 ——————- 0
0.8 * 2 = 1.6 ——————- 1
0.6 * 2 = 1.2 ——————- 1 我们可以发现在该计算中已经出现了循环，0.6用二进制表示为 1001 1001 1001 1001 ……
如果是10.6，那个10.6的完整二进制表示为 1010.100110011001……
0.6 = 1 * 2^-1 + 0 * 2^-2 + 0 * 2^-3 + 1 * 2^-4 + ……
2^-1=1/2=0.5
2^-2=1/4=0.25
2^-3=1/8=0.125
......
三、二进制转单精度浮点数公式：
方便区分假设下面是float 的二进制数：
0100 0000 0100 0000 0000 0000 0000 0000
0: 符号位----记为S 0 为正数 1 为负数 1bit
100 0000 0 ：阶码---记为E 8bit
100 0000 0000 0000 0000 0000 ：尾数位 ---记为M 23bit
公式： （-1）^s *（1.M）*2^(M-127)
四、二进制转单精度浮点数案例：
十六制： 41360000
二进制： 0100 0001 0011 0110 0000 0000 0000 0000
S 0：代表正数
E：100 0001 0 =130
(M-127)=130-127=3
M ：1. 011 0110 0000
1. 011 0110 0000 ^3= 1011.0110 = 11.375
五、小数转二进制（参考上面小数是怎么转换的）：
我们将十进制的4.5转换成二进制: 100.1
他的科学计数法即：1.001*2^2
即M= 0010 0000 0000 0000 0000 000
E= 127+2=129 = 1000 0001
S=0（正数）
4.5f 二进制表示 0 1000 0001 0010 0000 0000 0000 0000 000
六、代码实现(注意高低位 ，高位在后代码中)
/**
*将byte数组数据转换成float* @param arr
*@return*/
public static float bytes2Float(byte[] arr) {
int accum = 0;
accum = accum | (arr[0] & 0xff) << 0;
accum = accum | (arr[1] & 0xff) << 8;
accum = accum | (arr[2] & 0xff) << 16;
accum = accum | (arr[3] & 0xff) << 24;
return Float.intBitsToFloat(accum);
}
七、不足之处、烦请各位大佬批评指正。
