树中每个节点都有一个值，用下标从 0 开始、长度为 n 的整数数组 cost 表示，其中 cost[i] 是第 i + 1 个节点的值。每次操作，你可以将树中 任意 节点的值 增加 1 。你可以执行操作 任意 次。

你的目标是让根到每一个 叶子结点 的路径值相等。请你返回 最少 需要执行增加操作多少次。

注意：

• 满二叉树 指的是一棵树，它满足树中除了叶子节点外每个节点都恰好有 2 个节点，且所有叶子节点距离根节点距离相同。
• 路径值 指的是路径上所有节点的值之和。

 

示例 1：

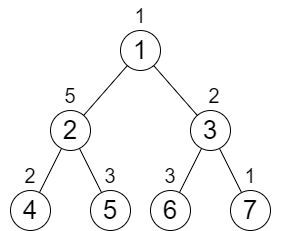
输入：n = 7, cost = [1,5,2,2,3,3,1]
输出：6
解释：我们执行以下的增加操作：
- 将节点 4 的值增加一次。
- 将节点 3 的值增加三次。
- 将节点 7 的值增加两次。
从根到叶子的每一条路径值都为 9 。
总共增加次数为 1 + 3 + 2 = 6 。
这是最小的答案。

示例 2：

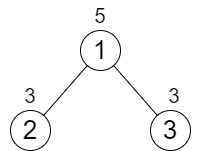
输入：n = 3, cost = [5,3,3]
输出：0
解释：两条路径已经有相等的路径值，所以不需要执行任何增加操作。

 

提示：

• 3 <= n <= 105
• n + 1 是 2 的幂
• cost.length == n
• 1 <= cost[i] <= 104

```cpp
class Solution {
public:
    vector<int> maxSum;
    int maxPathSum(int root, int n, vector<int>& cost) {
        if (root * 2 > n) {
            maxSum[root -1] = cost[root -1];
            return cost[root -1];
        }
        if (maxSum[root - 1] != 0) return maxSum[root - 1];
        int maxLeft = maxPathSum(root * 2, n, cost);
        int maxRight = maxPathSum(root * 2 + 1, n, cost);
        maxSum[root -1] = cost[root - 1] + max(maxLeft, maxRight);
        return maxSum[root -1];
    }
    int minIncrements(int n, vector<int>& cost) {
        maxSum.resize(n, 0);
        maxSum[0] = maxPathSum(1, n,  cost);

        queue<vector<int>> q;
        q.push({1, cost[0]});
        int maxV = maxSum[0];
        int ans = 0;
        while(!q.empty()) {
            auto top = q.front(); q.pop();
            int idx = top[0];
            int curSum = top[1];
 
            if (2 * idx > n) continue;
            if (curSum + maxSum[2 * idx - 1] == maxV) {
                q.push({2 * idx, curSum + cost[2 * idx -1]});
            }
            else {
                int tmp  =  (maxV - curSum - maxSum[2 * idx - 1]);
                ans += tmp;
                q.push({2 * idx, curSum + cost[2 * idx -1] + tmp});
                
            }

            if (curSum + maxSum[2 * idx] == maxV) {
                q.push({2 * idx + 1, curSum + cost[2 * idx]});
            }
            else {
                int tmp2  =  (maxV - curSum - maxSum[2 * idx]);
                ans += tmp2;
                q.push({2 * idx + 1, curSum + cost[2 * idx] + tmp2});
                
            }
        }
        return ans;
        
    }
};