什么是巴特沃斯滤波器？

巴特沃斯滤波器最先由英国工程师斯蒂芬·巴特沃斯（Stephen Butterworth）在1930年发表在英国《无线电工程》期刊的一篇论文中提出的。
巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦，没有起伏，而在阻频带则逐渐下降为零。在振幅的对数对角频率的波特图上，从某一边界角频率开始，振幅随着角频率的增加而逐步减少,趋向负无穷大。一阶巴特沃斯滤波器的衰减率为每倍频6分贝，每十倍频20分贝。二阶巴特沃斯滤波器的衰减率为每倍频12分贝、三阶巴特沃斯滤波器的衰减率为每倍频18分贝、如此类推。巴特沃斯滤波器的振幅对角频率单调下降，并且也是唯一的无论阶数，振幅对角频率曲线都保持同样的形状的滤波器。只不过滤波器阶数越高，在阻频带振幅衰减速度越快。其他滤波器高阶的振幅对角频率图和低阶数的振幅对角频率有不同的形状。
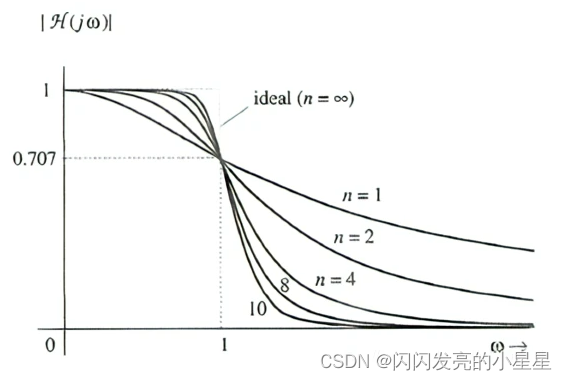
在这里插入图片描述
Butterworth 滤波器的幅值响应在通带内具有最大平坦度，并在整体上呈现单调性。这种平滑是以降低滚降陡度为代价的。对于给定滤波器阶数，椭圆和 Chebyshev 滤波器通常提供更陡的滚降。

butter 使用一个五步算法：

1.它使用函数 buttap 查找低通模拟原型的极点、零点和增益。
2.它将极点、零点和增益转换为状态空间形式。
3.如果需要，它使用状态空间变换将低通滤波器转换为具有所需频率约束的带通、高通或带阻滤波器。
4.对于数字滤波器设计，它使用 bilinear 通过具有频率预修正的双线性变换将模拟滤波器转换为数字滤波器。经过仔细调整频率，模拟滤波器和数字滤波器在 Wn 或 w1 和 w2 处可具有相同的频率响应幅值。
根据需要，它将状态空间滤波器转换回其传递函数或零极点增益形式。

参考：butterWorth

滤波器的阶数的含义

滤波器的阶数是指在滤波器的传递函数中有几个极点。阶数同时也决定了转折区的下降速度，一般每增加一阶(一个极点)，就会增加一20dBDec(一20dB每十倍频程)。
如上图所示，阶数越高，衰减速度越快。

matlab中的butter

参考：Butterworth 滤波器设计
语法：

[b,a] = butter(n,Wn)
[b,a] = butter(n,Wn,ftype)
[b,a] = butter(n, [w1 w2],ftype)
[z,p,k] = butter(___)
[A,B,C,D] = butter(___)

说明：

n — 滤波器阶数，滤波器阶数，指定为整数标量。对于带通和带阻设计，n 表示滤波器阶数的一半。
Wn — 截止频率截止频率，指定为标量或二元素向量。截止频率是滤波器幅值响应为 1 / √2 时的频率。 Wn = 截止频率*2/采样频率
如果 Wn 是标量，则 butter 用于设计截止频率为 Wn 的低通或高通滤波器。
如果 Wn 是二元素向量 [w1 w2]，其中 w1 < w2，则 butter 用于设计截止频率下限为 w1 且截止频率上限为 w2 的带通或带阻滤波器。
对于数字滤波器，截止频率必须介于 0 与 1 之间，其中 1 对应于奈奎斯特速率（即采样率的一半）或 π 弧度/采样点。
对于模拟滤波器，截止频率必须用弧度/秒表示，并且可以取任何正值。
ftype — 滤波器类型 ‘low’ | ‘bandpass’ | ‘high’ | ‘stop’

示例：
低通 Butterworth 传递函数
设计截止频率为 300 Hz 的 6 阶低通 Butterworth 滤波器，对于以 1000 Hz 的速率采样的数据，截止频率对应于 0.6π 弧度/采样点。绘制其幅值和相位响应。用它对长度为 1000 个采样的随机信号进行滤波。

fc = 300;
fs = 1000;

[b,a] = butter(6,fc/(fs/2));

freqz(b,a,[],fs)

subplot(2,1,1)
ylim([-100 20])

在这里插入图片描述

dataIn = randn(1000,1);
dataOut = filter(b,a,dataIn);

ps：freqz:数字滤波器的频率响应

scipy.signal butter 中有哪些参数，各参数分别是什么含义？

scipy.signal.butter

scipy.signal.butter(N, Wn, btype='low', analog=False, output='ba', fs=None)[source]

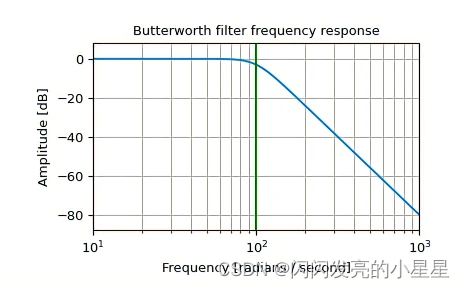
在这里插入图片描述

示例1：

from scipy import signal
import matplotlib.pyplot as plt
import numpy as np
b, a = signal.butter(4, 100, 'low', analog=True)
w, h = signal.freqs(b, a)
plt.semilogx(w, 20 * np.log10(abs(h)))
plt.title('Butterworth filter frequency response')
plt.xlabel('Frequency [radians / second]')
plt.ylabel('Amplitude [dB]')
plt.margins(0, 0.1)
plt.grid(which='both', axis='both')
plt.axvline(100, color='green') # cutoff frequency
plt.show()

在这里插入图片描述
示例2：
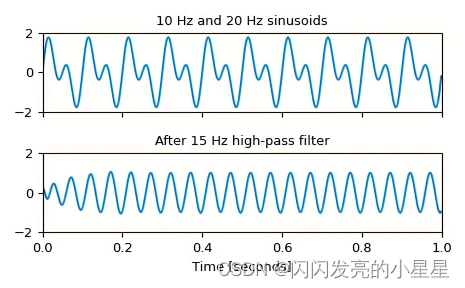
Generate a signal made up of 10 Hz and 20 Hz, sampled at 1 kHz

t = np.linspace(0, 1, 1000, False)  # 1 second
sig = np.sin(2*np.pi*10*t) + np.sin(2*np.pi*20*t)
fig, (ax1, ax2) = plt.subplots(2, 1, sharex=True)
ax1.plot(t, sig)
ax1.set_title('10 Hz and 20 Hz sinusoids')
ax1.axis([0, 1, -2, 2])

Design a digital high-pass filter at 15 Hz to remove the 10 Hz tone, and apply it to the signal. (It’s recommended to use second-order sections format when filtering, to avoid numerical error with transfer function (ba) format):

sos = signal.butter(10, 15, 'hp', fs=1000, output='sos')
filtered = signal.sosfilt(sos, sig)
ax2.plot(t, filtered)
ax2.set_title('After 15 Hz high-pass filter')
ax2.axis([0, 1, -2, 2])
ax2.set_xlabel('Time [seconds]')
plt.tight_layout()
plt.show()