一、前言

三年前我就折腾过一维下料问题了，当时查遍百度、谷歌，阅尽硕博论文，最终采用自研算法解决了一维下料问题，详见“一维下料问题的研究”，算法演示详见“EasyCut一维下料系统”。当时也阅读了大量使用遗传算法解决该问题的论文，但由于效果比较差，最终放弃了该算法。

当时我还“大言不惭”的对一些论文进行了如下“批判”：

遗传算法能对下料方案有一定程度的优化，但是优化不明显，或许是哪个算子设计不合理、或者参数没有调到合适的值。（注：相关的论文中，结果数据非常优秀，但本人无法调出那么优秀的方案，所以对有些论文报怀疑态度）。

近期空下来，重拾了遗传算法，并进行了试验，下料结果较三年前有所突破。虽然比起我的自研算法还有不小差距，但起码为一维下料又贡献了一丢丢思路，也算为研究此算法的同志抛砖引玉一下。

二、概念

下料：有若干规格的原材料，要切割成一批若干规格的零件，确定一种切割方式，使得原材料用料最少、产生的废料最少。

一维下料：上面提到的规格，可以包含很多属性，比如：长度、宽度、厚度等等。所谓一维下料，只关注其中一种属性，而其它属性被认为全部相同，这样便大大降低了下料问题的处理难度。本文研究的一维下料，以长度作为优化目标。

三、术语定义

原料：用于切割的原材料，长度不定。

零件：从原料中切割下来的短料，长度不定。

废料：一根原料被使用后，剩余长度无法再用于生产任意零件。

余料：一个原料被使用后，剩余材料仍然可以在后续生产中进行零件切割。

四、问题描述

现有N段长度不等的原料（当然，也可以全部长度相等或者其中一部分长度相等），现需要切割为M段长度不等的零件，生成一种切割方案，使产生的废料最少、原料利用率最高。

五、实现思路

1、遗传算法

我们先梳理一遍遗传算法。本节基本就是遗传算法相关的八股文了，但为了后续分析，我们还是需要把概念说明白。

实际上，遗传算法就是你想的那个意思，明白了吧哈哈哈。

说点儿正经的，遗传算法的思想就是基于达尔基的。。。，不是，高尔文的。。。，不是，达尔文的进化论：适者生存、优胜略汰。那么通俗的讲，就是一个物种群体，通过一代一代的进化，最后留下来的是精英。对应到我们的算法中，这个精英就是我们追求的解。那么我们怎样把这个进化的过程抽象成计算机语言呢？伟大的算法专家为我们总结好了算法模型。

1）染色体

从生物学角度来说，每一个生物个体都有一个自己独特的染色体。遗传算法将一条解，抽象成一个染色体。所以遗传算法的最终目标，是通过一代一代的进化，找到一个最优的染色体。

2）种群

所谓种群，就是由多个生物个体，组成的一个群体。也可以简单的理解成，种群就是由一批染色体组成的群体。

从生物学角度理解，只有群体生物才能一代一代慢慢进化，或者反过来说，如果只有一个生物个体，它来不及进化可能就灭绝了。

3）交叉算子

简单理解为，两个雌雄个体，繁衍出一个新的个体。具体怎么繁衍，你懂得。

4）变异算子

简单理解为，没有变异，就没有进化。

5）选择算子

选择优秀个体让其生存下来，参与下一代的进化。

2、一维下料和遗传算法结合

一维下料到底应该如何基于遗传算法实现呢？我们分别从以上提到的五个点进行介绍。

1）染色体

由上面的分析可知，一个染色体就代表一个解，所以我们可以使用以下结构来表示一条染色体。

//染色体
public class Chromosome {
    //一个染色体包含多个元素
    private List<Element> representation;
}

//元素
public class Element {
    //原料长度
    private Integer rawLength;
    //本原料上切哪些零件
    private List<Integer> partList;
    //本原料的使用率
    private BigDecimal usedRate;
    //本原料的余料
    private Integer remainLength;
}

2）种群

如何生成初始种群？从遗传算法的原理可知，无论是交叉、还是变异、或者选择，都有随机的影子，那咱就干脆随机到底，种群初始化也使用随机策略。随机生成一群“质量”还算可以的种群，让他们进化。

3）交叉算子

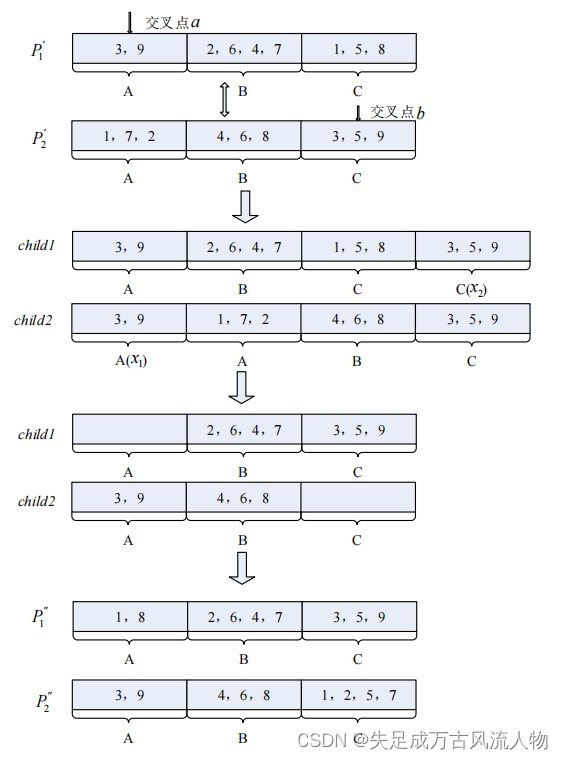
交叉的实质是将两个染色体，其中的部分元素进行交叉替换，形成新的染色体。这个算子的设计，我参考了一批硕士论文，交叉过程有些复杂，下面我贴一张论文中的原图来帮助理解。需要说明几点：

第一、P1'、P2'代表交叉前的两个染色体，P1''、P2''代表交叉后新生成的两个染色体；

第二、A、B、C代表三个原料，1-9代表9个零件；

第三、其它的内容，自己意会一下下图吧。