格雷编码

力扣链接：89. 格雷编码

题目描述

n 位格雷码序列是一个由 2n 个整数组成的序列，其中：
每个整数都在范围 [0, 2n - 1] 内（含 0 和 2n - 1）
第一个整数是 0
一个整数在序列中出现不超过一次
每对相邻整数的二进制表示恰好一位不同，且
第一个和最后一个整数的二进制表示恰好一位不同
给你一个整数 n ，返回任一有效的 n 位格雷码序列。

示例

输入：n = 2
输出：[0,1,3,2]
解释：
[0,1,3,2] 的二进制表示是 [00,01,11,10] 。

00 和 01 有一位不同
01 和 11 有一位不同
11 和 10 有一位不同
10 和 00 有一位不同
[0,2,3,1] 也是一个有效的格雷码序列，其二进制表示是 [00,10,11,01] 。
00 和 10 有一位不同
10 和 11 有一位不同
11 和 01 有一位不同
01 和 00 有一位不同

思路1——找规律

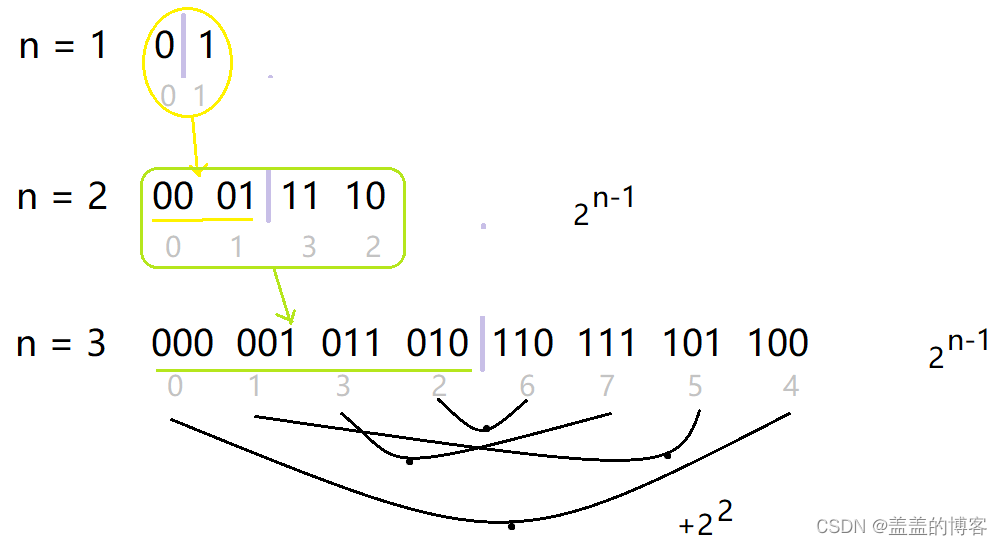
在这里插入图片描述

Java代码

class Solution {
    public List<Integer> grayCode(int n) {
        List<Integer> ans = new ArrayList<>();
        ans.add(0);
        int tmp = 1;
        for (int i = 0;i < n;i++){
            for (int j = ans.size() - 1;j > -1;j--){
                ans.add(ans.get(j) + tmp);
            }
            tmp *= 2;
        }
        return ans;
    }
}

思路2——懂原理

格雷编码的生成过程, G(i) = i ^ (i/2);
如 n = 3:
G(0) = 000,
G(1) = 1 ^ 0 = 001 ^ 000 = 001
G(2) = 2 ^ 1 = 010 ^ 001 = 011
G(3) = 3 ^ 1 = 011 ^ 001 = 010
G(4) = 4 ^ 2 = 100 ^ 010 = 110
G(5) = 5 ^ 2 = 101 ^ 010 = 111
G(6) = 6 ^ 3 = 110 ^ 011 = 101
G(7) = 7 ^ 3 = 111 ^ 011 = 100

Java代码

class Solution {
    public List<Integer> grayCode(int n) {
        List<Integer> ret = new ArrayList<>();
        for(int i = 0; i < 1<<n; ++i)
            ret.add(i ^ i>>1);
        return ret;
    }
}