《编程思维与实践》1060.浮点数加法

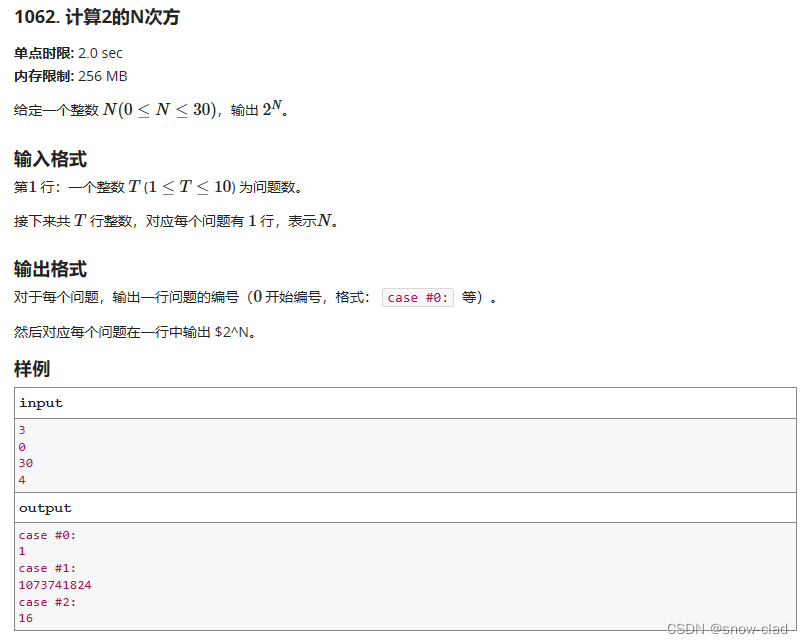
题目

思路

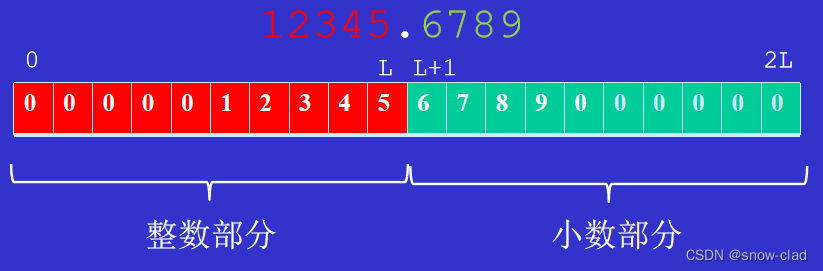
浮点数可以分为[整数部分].[小数部分],可以将两个部分分开处理,最后再合并,但在处理四舍五入时较为繁琐,

为了方便起见,这里采用将两个部分一起处理的方式:

由于浮点数不超过500位:整数部分最多500位,小数部分最多500位,

所以加法后的结果整数部分最多501位,小数部分最多500位.

所以可以宏定义L=500,数组最大长度为2L+1,其中[0,L]存整数部分,[L+1,2L+1]存小数部分;

具体步骤:

1.读取浮点数:

①有小数点:找到小数点的位置,小数点前逆向遍历存取整数部分,小数点后正向遍历存取小数部分;

②无小数点(遍历到字符串末尾):从字符串末尾逆向遍历存整数部分.

2.浮点数加法:

先将保留位(N位)后的部分相加,进位后判断保留位的后一位是四舍还是五入;

再将保留位和前面的部分相加,最后进行进位.

3.输出浮点数:

整数部分去除前置0,如果整数部分全为0则输出整数0.

代码

#include<stdio.h>
#include<stdlib.h> 
#include<string.h>
#define L 500

void carry(int *a,int bin);  //进位 
void Input(int *a);   //处理浮点数输入
void add(int *a,int *b,int N);  //顺序加 a+=b
void output(int *a,int N);  //输出

int main()
{
	int A[2*L+1]={0},B[2*L+1]={0},N;
	Input(A);
	Input(B);
	scanf("%d",&N);
	add(A,B,N); 	//A+=B
	output(A,N);
	return 0;
}

void carry(int *a,int bin)  //进位 
{
	int flag=0;
	for(int i=2*L;i>=0;i--)
	{
		int temp=a[i]+flag;
		a[i]=temp%bin;
		flag=temp/bin;
	}
}

void Input(int *a)   //input a float number
{
    char s[L+1];
    scanf("%s",s);    
    int i=0;
    while(i<strlen(s)&&s[i]!='.') //无小数点和有小数点的情况
	{
		i++; 	//定位小数点
	}
    for(int j=i-1,k=L;j>=0;j--) 
    {
    	a[k--]=s[j]-'0';  //整数部分
	}
    for(int j=i+1,k=L+1;j<strlen(s);j++) 
    {
    	a[k++]=s[j]-'0';   //小数部分
	}
}

void add(int *a,int *b,int N)  //顺序加 
{   
	int i;
    for(i=2*L;i>L+N;i--)
    {
        a[i]+=b[i];
    }
    carry(a,10);
    if(a[i+1]>=5)  //保留位的下一位
    {
    	a[i]++;  //四舍五入 
	}
    for(i=L+N;i>=0;i--)
    {
        a[i]+=b[i];
    }
    carry(a,10);
}

void output(int *a,int N)
{
    int i=0;
    while(i<=L&&a[i]==0)
	{
		i++;  //跳过前置0
	}
    if(i>L)   //整数部分全为0
	{
		printf("0");   
	}
    else
    {
        while(i<=L)
		{
			printf("%d",a[i++]);  //整数部分
		}
    }
    printf(".");
    while(i<=L+N)
	{
		printf("%d",a[i++]);  //小数部分
	}
}