不同坐标系之间的刚性转换以及实现：

坐标系转换原理如下，使用了仿射变换实现了旋转平移：
$$\left[\begin{array}{ccc}{r}_{11}& r_{12}& t_x\\ r_{21}& r_{22}& t_y\\ 0& 0& \end{array}\right]\ast \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{c}{x}^{{}^{\prime }}\\ y^{{}^{\prime }}\\ 1\end{array}\right]$$
但是在eigen中求取方程式$A\ast x=b$,所以前面可以将$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]$看成是A，把$\left[\begin{array}{c}{x}^{{}^{\prime }}\\ y^{{}^{\prime }}\\ z^{{}^{\prime }}\end{array}\right]$看成是$b$。不过这样公式就需要一定的变形才能和前面的对应起来，前后做一个转置，如下所示：
$$\begin{gathered} {\left[\left[\begin{array}{ccc}{r}_{11}& r_{12}& t_x\\ r_{21}& r_{22}& t_y\\ 0& 0& \end{array}\right]\ast \\ \left[\begin{array}{c}x\\ y\\ 1\end{array}\right] \\ \right]}^T={\left[\begin{array}{c}{x}^{{}^{\prime }}\\ y^{{}^{\prime }}\\ 1\end{array}\right]}^T \end{gathered}$$
那么就会转换成如下所示：
$$\left[\begin{array}{ccc}x& y& 1\end{array}\right]\ast \left[\begin{array}{ccc}{r}_{11}& r_{21}& 0\\ r_{12}& r_{22}& 0\\ t_x& t_y& 1\end{array}\right]=\left[\begin{array}{ccc}{x}^{{}^{\prime }}& y^{{}^{\prime }}& 1\end{array}\right]$$
所以最终在程序里使用的是上面的公式，调用A.fullPivLu().solve(B)计算的时候也是A对应$\left[\begin{array}{ccc}x& y& 1\end{array}\right]$，B对应的就是$\left[\begin{array}{ccc}{x}^{{}^{\prime }}& y^{{}^{\prime }}& 1\end{array}\right]$。所以得出来的结果也是$\left[\begin{array}{ccc}{r}_{11}& r_{21}& 0\\ r_{12}& r_{22}& 0\\ t_x& t_y& 1\end{array}\right]$。看自己需求是否对其转置

A << -4.93374, -0.056378, 1, 0.397714, -0.126519, 1, 2.63284, -0.0925265, 1;
	B << 109995, 8318, 1, 110066, 13650, 1, 110032, 15885, 1;
Eigen::Matrix3d T = TransMatrix(A, B);
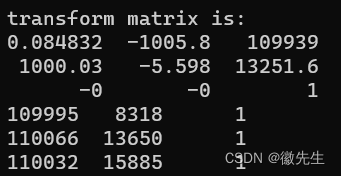
cout << "transform matrix is: " << "\n";
cout << T.transpose() << endl;//显示出A*T=B，但是实际计算的是（T的转置*A的转置）的转置=B的转置
cout << A*T << endl;

转换矩阵结果如下所示：