在第二章中讨论的安全叫信息理论安全或完美安全,因为他们的安全性是基于敌手没有足够的信息来成功地完成攻击,而不管敌手地计算能力。
计算安全比信息理论安全要稍微弱一些,也是大多数现代密码学构造方法的目标。由于完美安全所需密钥的长度过长,其他的密码学任务也有着类似的消极结论。所以为了获得实用的密码学方案,要考虑稍弱一些,但是仍有意义的安全定义
Kerckhoffs提出实践上不可破译的方案,基于计算的方法包含了两种放宽的完美安全概念:

具体量化方法:令t,<=1,大体将会是以下的形式:


渐进方法:

n只有足够大的时候,才能保证安全,以下为例子:


密钥越长,安全程度越高

松弛的必要性:
1.计算安全仅仅抵抗有效的即多项式实际的敌手
2.允许小的成功概率
一个结论:在任意加密方案中,密钥空间必须足够大,以至于敌手不能够遍历,且密钥空间的规模必须为安全参数的超多项式
函数f是可忽略的概念:

可忽略函数的一些性质:
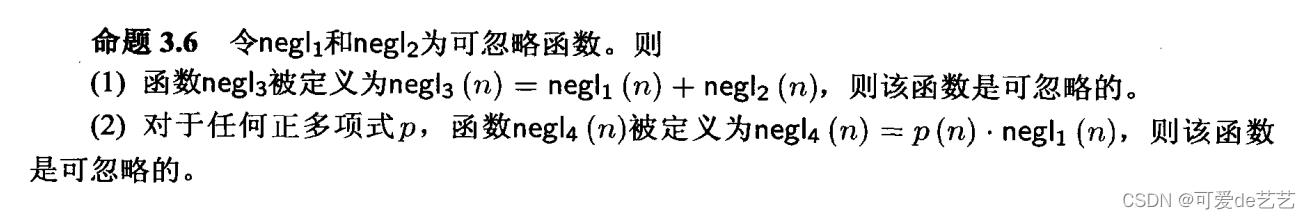
其中第二条性质表示如果可忽略函数被执行多次还是可忽略的
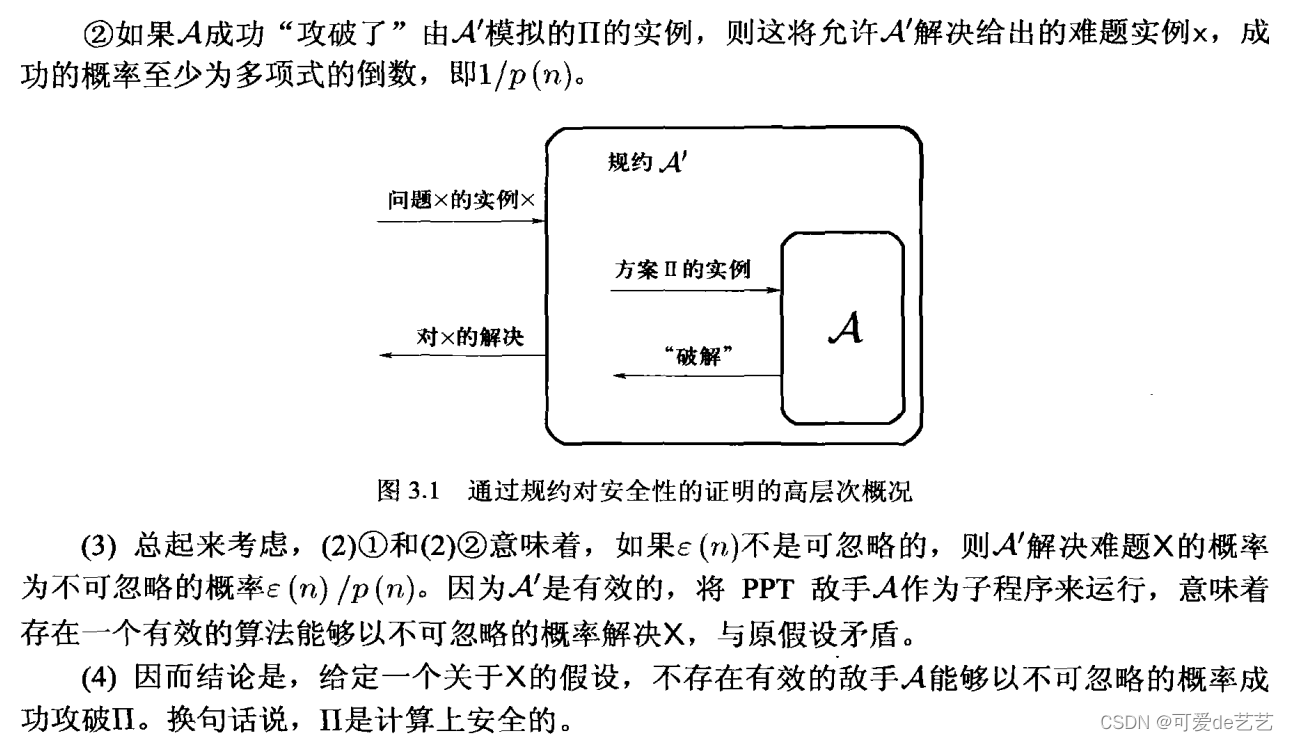
规约证明:
从假设开始,假设某个难题X不能通过任何多项式时间算法以不是可忽略的概率被解决,想要证明某个密码构造是安全的,做法如下: