目录
1.堆的概念
2.堆的创建
3.堆的插入与删除
3.1堆的插入
3.2堆的删除
1.堆的概念
如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0,1,2…,则称为 小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆
注意:堆是一棵完全二叉树
2.堆的创建
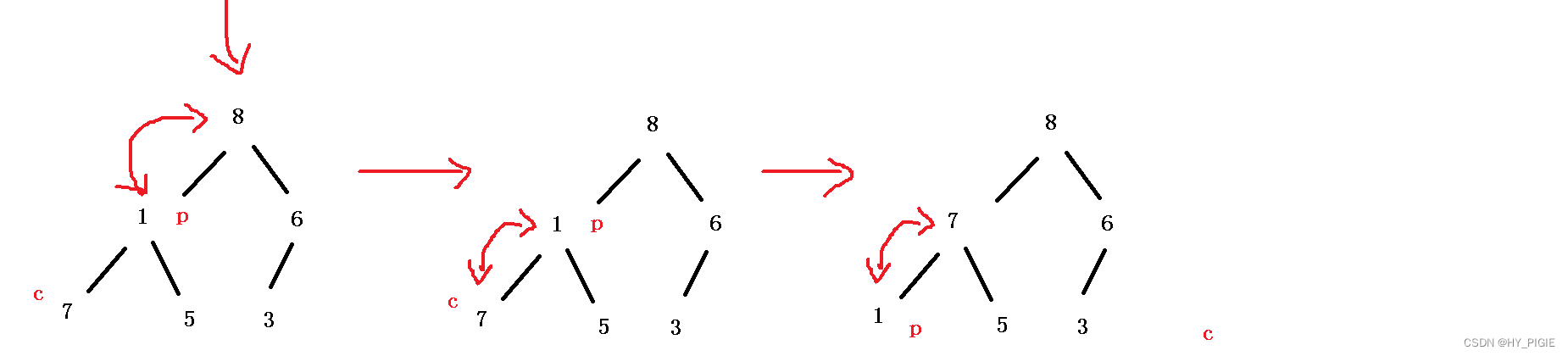
在堆这种数据结构中,可以看成每三个元素构成的一个子树为单位来观察。所以我们要调节的是每一个子树的父亲节点与孩子节点之间的关系
对于大根堆,我们需要维护父亲节点比孩子节点都大
对于小根堆,我们需要维护父亲节点比孩子节点都小
我们可以从最后一棵子树开始,先得到其父亲节点与孩子节点,再比较其关系进行位置上的调整。调整完此子树后,因为我们是从下往上开始遍历,变动了一棵树的位置就可能影响到其他子树的关系,所以我们需要维护其下方子树也应为一个大/小根堆
需要将父亲节点的位置移动到孩子节点的位置,孩子节点移动到下一棵子树的孩子节点位置中
对于父亲节点与孩子节点的数组下标关系为:
(在找孩子节点的时候,因为堆是一棵完全二叉树的原因,可能没有右孩子。所以我们首先搜寻的是其左孩子节点)
parent:父亲节点的下标
child:左孩子节点的下标
parent = (child - 1) / 2;
chile = parent * 2 + 1;
下面是建立大根堆的图演示

代码演示:
import java.util.Arrays;
public class Heap {
public int[] elem;
public static int usedSize;
public Heap(int[] elem) {
this.elem = new int[10];//初始长度为10,后面可以考虑扩容
}
//创建一个大根堆
public void createHeap(int[] array){
//首先要放到elem数组中,还可以得到其元素个数
for(int i = 0; i < array.length; i++){
this.elem[i] = array[i];
usedSize++;
}
//开始创建大根堆
//首要要找到其最后一棵子树的父亲节点
//parent = (child - 1) / 2
//最后一棵子树,肯定包含有数组中的最后一个节点
//所以我们可以通过最后一个元素的下标来得到父亲节点的下标
//从最后一棵子树开始,遍历每一颗子树,每一颗子树父亲节点在数组中相邻
//直到父亲节点的下标小于0下标
for(int parent = (usedSize - 1 - 1) / 2; parent >= 0; parent--){
//我们将维护子树状态的方法称为向下调整
shiftDown(parent,usedSize);
}
}
//向下调整
private void shiftDown(int parent, int len) {
//向下调整是,维护子树的状态
//因为调整了节点的关系,可能也会影响其他子树,所以要调整与此子树相关的下方的子树
//可以用过parent = child的方法来跳跃到其他子树
//直到child越界
int child = parent * 2 + 1;//得到左子树的下标
while(child < len){
//第一步,查看左右孩子节点的大小关系
//按需则取,再与父亲节点比较
//当然是在确保拥有右孩子的前提下
if(child + 1 < len && elem[child] < elem[child + 1]){
//因为我们创建的是大根堆
//在右孩子比左孩子大的时候,我们的child位置需要跳转到右孩子
child = child + 1;//child的位置从左孩子跳到右孩子
}
//再与父亲节点比较
if(elem[child] > elem[parent]){
//交换
int tmp = elem[child];
elem[child] = elem[parent];
elem[parent] = tmp;
//向下调整
//父亲节点跳转到孩子节点
//孩子节点根据跳转后的父亲节点的下标进行转换
parent = child;
child = parent * 2 + 1;
}else{
break;//因为我们是从下往上调整的,只要此树满足了大根堆
//就不需要变动节点的位置,也就意味着不会影响已经调整好了的其他子树
//所以可以直接break
}
}
}
public static void main(String[] args) {
int[] array = {1,5,3,7,8,6};
Heap heap = new Heap(array);
heap.createHeap(array);
System.out.println(Arrays.toString(heap.elem));
}
}结果为:

3.堆的插入与删除
3.1堆的插入
堆的插入是插在队尾的,即当作此数组的最后一个元素。
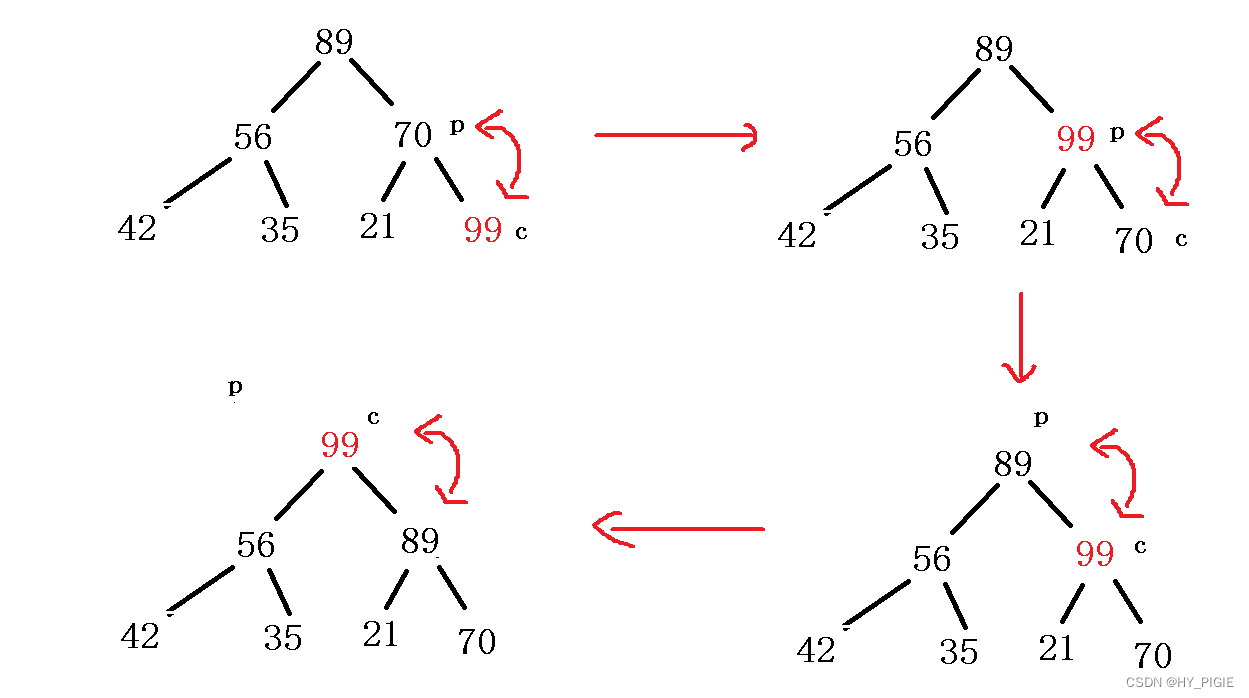
插入一个元素后,要维持其依然为一个大/小根堆,所以需要调整。但元素是在队尾的,就不能用之前的向下调整了,此处运用的是向上调整。将插入的元素逐步向上转移,安插到一个合适的位置。
以大根堆为例:
代码演示:
public void push(int val){
if(isFull()){//如果满了就要扩容
elem = Arrays.copyOf(elem,2*elem.length);
}
this.elem[usedSize++] = val;
shiftUp(usedSize - 1);
}
public void shiftUp(int child){
int parent = (child - 1) / 2;
//实际上就是把新插入的数值当成child,一直推着其往上移动,直到找到一个合适的地方
while(child > 0){
if(elem[child] > elem[parent]){
int tmp = elem[child];
elem[child] = elem[parent];
elem[parent] = tmp;
child = parent;
parent = (child - 1) / 2;
}else{
break;
}
}
}
public boolean isFull() {
return usedSize == elem.length;
}3.2堆的删除
关于堆的删除,堆只能删除其最后一个元素。
首先把最后一个元素放到0下标即堆顶的位置,再使usedSize-1,达到删除的效果.
为了维持堆的特性,我们将新换到堆顶的元素使用向下调整,将其安插到合适的地方
public void poll() {
if(empty()) {
throw new RuntimeException("堆为空");
}
//交换最后一个元素和第一个元素的位置
int tmp = elem[0];
elem[0] = elem[usedSize-1];
elem[usedSize-1] = tmp;
usedSize--;//总元素-1,无法读取,达到删除的效果
shiftDown(0,usedSize);//将新换到堆顶的元素向下调整
}
public boolean empty() {
return usedSize == 0;
}