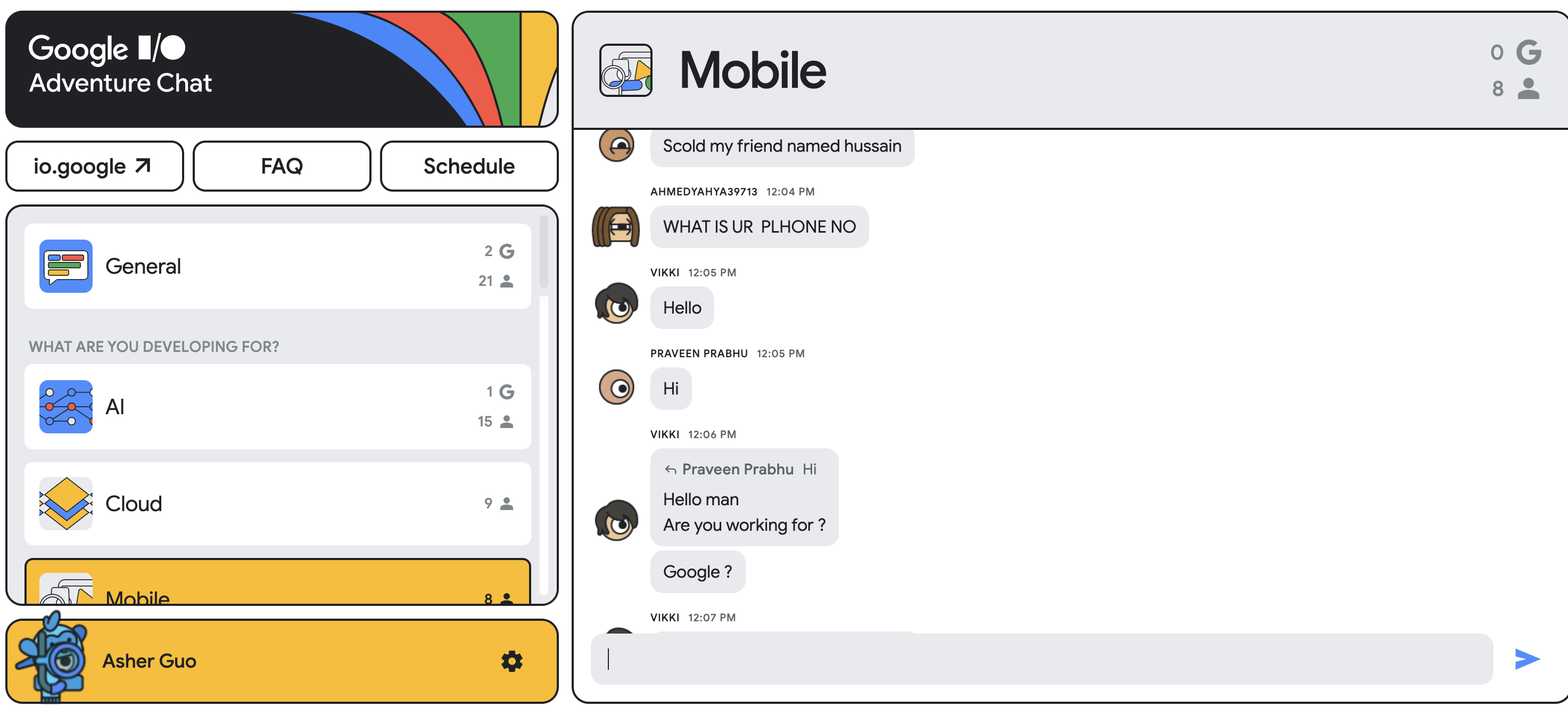
1 电脑的工作原理:
电脑是由各种不同的硬件组成,由驱动软件驱使硬件进行工作。所有的软件工程师都会直接或者间接的使用到驱动。
定义:是一个图形库,用于渲染2D、3D矢量图形的跨语言、跨平台的应用程序编程接口 (API)。针对GPU。

应用端:即我们自己的程序端,相对于opengl es,我们属于应用端
图元:要渲染的几何物体,或者形状。比如要渲染一个正方形的图片,就是一个图元,要渲染两)直线,这两条直线也是图元
纹理:通俗点,可以理解为一张图片,在opengles中纹理就是图片的另外一种叫法纹素:
纹理的基础单元,也就是像素.
顶点数组:顶点指的是组成图元的各个顶点的坐标数据(在3D笛卡尔坐标中即x,y,z坐标),这些坐标数可以一起存到一个内存数组中,这个数组就叫做顶点数组.
顶点缓冲区: 在显存中专门分配一块显存来存储这个顶点数组,这.个显存就称为顶点缓冲区
顶点着色器(大家通过前面几节课都知道了,就不复诉了)片元着色器.
Khronos 定义了OpenGL 微软自己定义了DirectX目前手机,不管是 ioS 还是 Android,都是支持 OpenGL ES电脑:Windows 系统支持 DirectX 和 OpenGL,Linux/Mac(Unix)系统支持OpenGL。
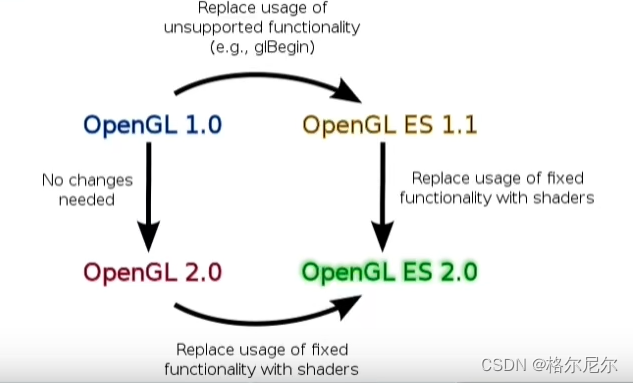
20 世纪 90 年代——OpenGL 开放
2000 年——openGL ES 开放
2005 年——OpenGL SC 开放
2008 年——开放基层更高效计算的 OpenCL
2014 年——开放 SPIR
2015 年——Vulkan 开放,更加高效的 GPU 使用效率
2 OPENGL ES
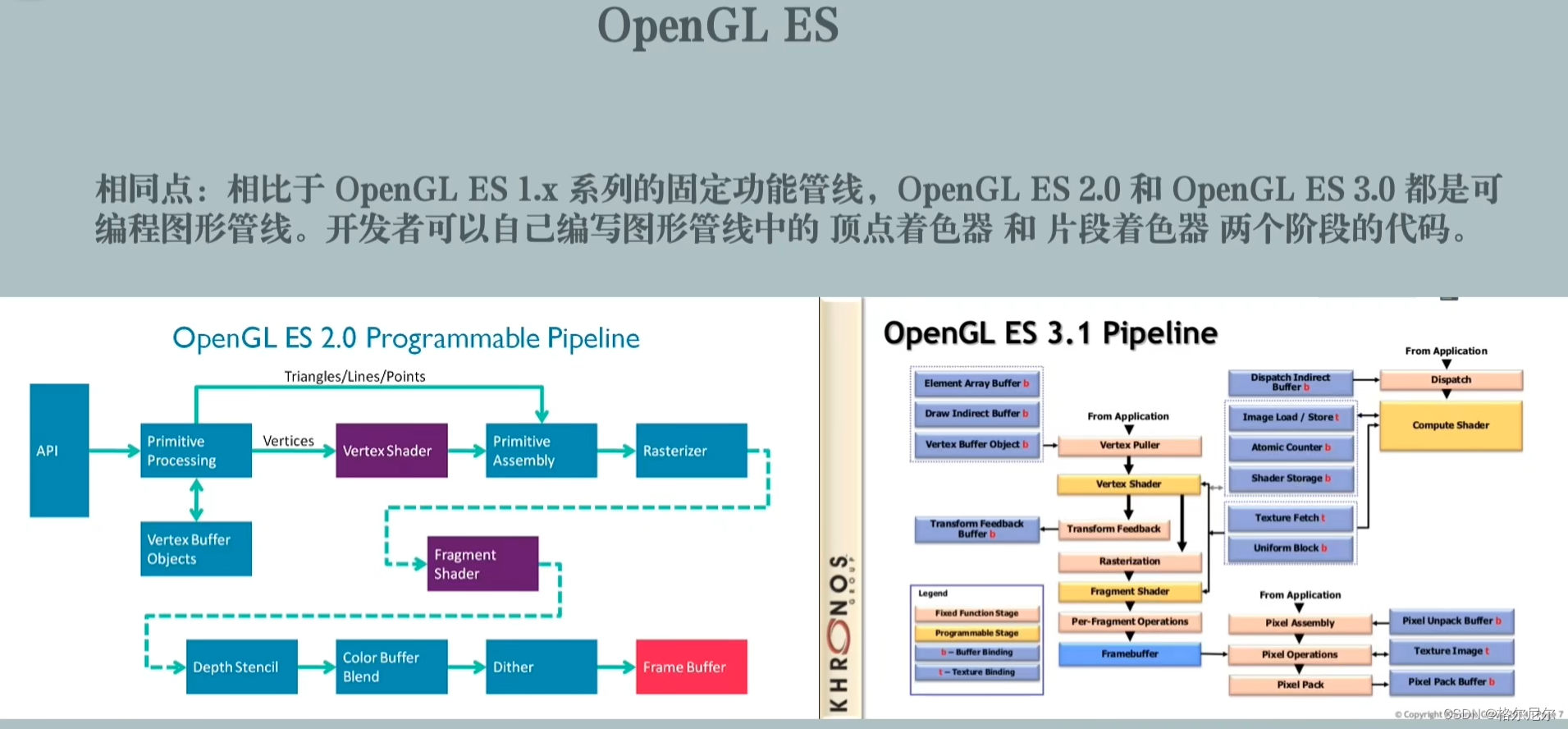
3 OpenGL ES不同点
1.兼容性:
3.0是可以兼容2.0的
2.新特性
采用阴影贴图,体渲染,基于GPU的粒子动画,几何形状实例化,纹理压缩,伽马校正等这些重要功能在2.0是没有的。3.0将其引入,同时继续适应嵌入系统的局限性。
3.渲染管线
3.0中移除了Alpha测试(ES 2.0)和逻辑操作(ES 1.x),片元着色器可以抛弃片段所以Alpha测试可在片元着色器中进行,逻辑操作则是因其较少使用;
4.着色器脚本编写
有几点比较大的变化:
(1)版本声明
必须在着色器脚本中使用#version 300es声明为指定使用OpenGLES3.0版本
#version 300 es
layout(location=0)in vec4 vPosition;
void main(){
gl_Position = vPosition;
}
不添加版本声明或者使用#version 100 es声明版本则指定使用OpenGL ES 2.0.
(以往2.0刚出来可编程图形管线,版本声明为#version 100 es,后为了与版本号匹配,3.0的shader版本直接从100es跳到300es,故不存在200es)
(2)输入输出
3.0新增in,out,inout关键字,用于取代attribute和varying关键字。同时gl_FragColor和gl_FragData被删除,片元着色器可使用out声明字段输出。
#version 300 es
layout(location=0)in vec4 vPosition;
void main(){
gl_Position = vPosition;
}
(3)变量赋值
3.0中可以直接使用layout对指定位置变量赋值,
shader脚本中
layout(location=1)uniform float a;
代码中,直接写上对应layout值就可赋值
GLES30.glUniform1f(1,1f);
2.0中必须按以下形式赋值
GLES20.glUniform1f(GLES20,glGetAttribLocation(program,"a"),1f)
4 OpenGL ES 3.0新功能
OpenGL ES不同点
兼容性
OpenGL ES 3.0向后兼容OpenGL ES 2.0。即2.0编写的应用程序可以在3.0中继续使用
新特性
3.0采用了阴影贴图、体渲染( volume rendering ) 、基于GPU的粒子动画、几何形状实例化、纹理压缩和伽马校正等技术,同时继续适应嵌入系统的局限性。2.0中则不具备这些功能。
渲染管线
3.0中移除了Alpha测试和逻辑操作(LogicOp)两部分,这两部分存在于OpenGL ES2.0和 OpenGL ES 1.x中。
移除 Alpha测试是因为片段着色器可能抛弃片段,因此 Alpha测试可以在片段着色器中进行。移除逻辑操作( LogicOp)是因为它很少被使用。
着色器编写
版本声明:使用#version 100 es来声明为OpenGL ES 2.0版本,使用#version 300 es来生命为OpenGL ES 3.0版本。这是因为OpenGL ES 2.0是刚刚发布可编程图形管线的版本所以为100,而OpenGL ES 3.0为了匹配上版本号因此从1.0直接跳到了3.0。
输入输出:3.0中新增了in,out,inout 关键字,用来取代 attribute和varying 关键字。同时gl_FragColor和 gl FragData 也删除了,片段着色器可以使用out 声明字段输出。
变量赋值:3.0中可以直接使用layout对指定位置的变量赋值。代码中,直接写上对应的 layout的值就可以赋值。而2.0中必须使用GLES20.gluniform1f(GLES2e.glGetAttribLocation(program,“a”),1f)这样的形式来赋值。
5 OpenGL ES 3.0新功能
纹理:
sRGB纹理和帧缓冲区——允许应用程序执行伽马校正渲染。
2D纹理数组——保存一组2D纹理的纹理目标。
3D纹理——一些OpenGL ES 2.0实现通过扩展支持3D纹理,而OpenGL ES3.0将此作为强制的功能。
深度纹理和阴影比较——启用存储在纹理中的深度缓冲区。
无缝立方图——立方图可以进行采样如过滤来使用相邻面的数据并删除接缝处的伪像。
浮点纹理——支持并可以过滤半浮点纹理(16位),也支持全浮点纹理(32位),但不能过滤。
ETC2/EAC纹理压缩——OpenGL ES 3.0中强制支持ETC2/EAC格式。(ETC2/EAC的格式为RGB8,RGBA888和单通道及双通道有符号/无符号纹理数据)
整数纹理——OpenGL ES 3.0引人了渲染和读取保存为未规范化有符号或无符号8位、16位和32位整数纹理的能力。
其它纹理格式——OpenGL ES 3.0还包含了对特殊纹理格式的支持。(如11-11-10RGB浮点纹理、共享指数RGB 9-9-9-5纹理、10-10-10-2整数纹理以及8位分量有符号规范化纹理)
非2幂次纹理(NPOT)——纹理现在可以指定为不为2的幂次尺寸。
纹理细节级别(LOD)——现在可以强制使用用于确定读取哪个Mipmap的LOD参数。
纹理调配——允许独立控制纹理数据每个通道(R、G、B、A)在着色器中的映射。
不可变纹理——为应用程序提供在加载数据之前指定纹理格式和大小的机制。
最小尺寸增大——OpenGL ES 3.0支持远大于OpenGL ES 2.0的纹理资源。
着色器:
二进制程序文件——完全链接过的二进制程序文件可以保存为离线二进制格式,运行时不需要链接步骤。
强制的在线编译器——在OpenGL ES 3.0中,所有实现都有在线着色器编译器。
非方对阵——支持方阵之外的新矩阵类型,并在API中增加了相关的统一调用。
全整数支持——支持整数(以及无符号整数)标量和向量类型以及全整数操作。
质心采样——避免在多重采构时产生伪像。
平面/平滑插值程序——插值留序可以显式声明为平面或者平滑着色。
统一变量块——统一变量值可以组合为统一变量块,可以更高效地加载,共享。
布局限定符——显式绑定着色器源代码中的位置,还用于控制统一变量块的内存布局。
实例和顶点ID——可以在顶点着色器中访问顶点索引,实例渲染中访问实例ID。
片段深度——不依赖差值,显式控制当前片段的深度值。
新的内建函数——支持新的纹理功能、片段导数、半浮点数据转换和矩阵及数学运算。
宽松限制——着色器不再限于指令长度,支持变量为基础的循环和分支和数组索引.
几何形状:
变换反馈——可以在缓冲区对象中捕捉顶点着色器的输出。
布尔遮挡查询——应用程序可以查询绘制调用的任何像素是否通过深度测试。
实例渲染——有效地渲染包含类似几何形状但是属性(变化矩阵、颜色或者大小)不同的对象。
图元重启——允许特殊的索引值表示新图元的开始。
新顶点格式——支持更多新的顶点格式。(包括10-10-10-2有符号和无符号规范化顶点属性;8位、16位和132位整数属性;以及16位半浮点)
缓冲区对象:
统一变量缓冲区对象——为存储/绑定大的统一变量块提供高效的方法。
顶点数组对象——提供绑定和在顶点数组状态之间切换的高效方法。
采样器对象——将采样器状态(纹理循环模式和过滤)与纹理对象分离。
同步对象——为应用程序提供检查一组操作是否在GPU上完成执行的机制。
像素缓冲对象——使应用程序能够执行对像素操作和纹理传输操作的异步数据传输。
缓冲区子界映射——使应用程序能够映射缓冲区的一个子区域,供CPU访问。
缓冲区对象间拷贝——提供了高效地从不同的缓冲区对象互相传输数据的机制,不需要CPU干预。
帧缓冲区:
多重渲染目标(MRT)——允许应用程序同时渲染到多个颜色缓冲区。
多重采样渲染缓冲区——使应用程序能够渲染到具备多重采样抗锯齿功能的屏幕外帧缓冲区。
帧缓冲区失效提示——为应用程序提供了通知驱动程序不再需要帧缓冲区内容的机制。
新的混合方程式——新增支持最大值/最小值函数作为混合方程。