1 后缀表达式

        一种不需要括号的表达式方法，也把它称为 逆波兰表达式，是波兰逻辑学家卢卡西维奇（Lukasiewicz)发明的一种表示表达式的方法。

2 中缀表达式

        中缀表达式也就是我们常见的表达式书写方法，比如“8+(2-1)×3+5÷2”就是一个中缀表达式。

3 中缀表达式转后缀表达式

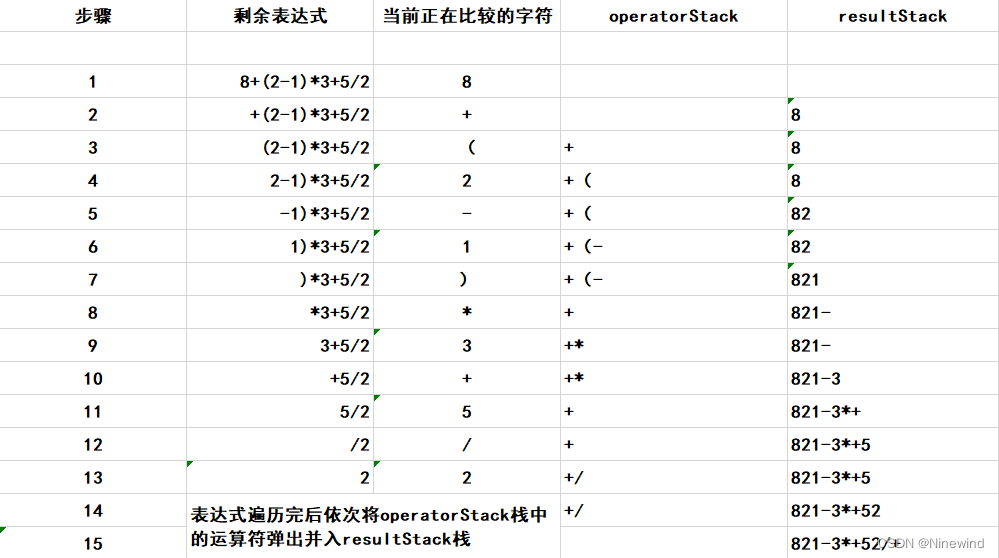
        中缀表达式转后缀表达式也就是将一个中缀表示的表达式转化成后缀表示的表达式。比如将中缀表达式“8+(2-1)×3+5÷2”转换成后缀表达式“8 2 1 - 3 * + 5 2 / +”。

3.1 方法---栈实现

1. 定义两个栈，一个resultStack用于存储最终得到的后缀表达式，一个operatorStack作为辅助栈用于存储符号。
2. 从左到右依次遍历中缀表达式的每一个数字和符号。
3. 若当前字符为数字，则当前数字入resultStack。结束当前字符的比较。
4. 若当前字符为“（  ”  或  operatorStack栈顶为空，则当前运算符入operatorStack。结束当前字符的比较。
5. 若当前字符是一个运算符 且 operatorStack栈顶不为空，并且优先级高于operatorStack栈顶的元素，则当前运算符入operatorStack。结束当前字符的比较。
6. 若当前字符是一个运算符 且 operatorStack栈顶不为空，并且优先级小于或等于operatorStack栈顶的元素。则弹出operatorStack栈顶的元素并将其入resultStack。（注意此时当前字符未入operatorStack栈）
7. 完成第6步后重新从第4步开始比较当前字符与operatorStack栈顶的元素。直到当前字符入operatorStack，结束当前字符的比较。
8. 若当前字符为“  ）”，则弹出operatorStack栈顶的元素，入resultStack栈。（注意此时“  ）”未丢弃）
9. 完成第8步后重新比较operatorStack栈顶的元素是否为“（  "。若不是，重新从第8步开始；若是，则弹出operatorStack栈顶的元素“（  "，丢弃“  ）”，结束当前字符的比较。
10. 中缀表达式遍历完后依次将operatorStack栈中的运算符弹出并入resultStack栈。

3.2 “8+(2-1)×3+5÷2”转换为“8 2 1 - 3 * + 5 2 / +”步骤图