一、将QT程序使用Release编译
二、新建一个文件夹,将Release编译生成的exe文件复制到新建文件夹中
先找到Release编译生成的exe文件夹位置,与项目创建的文件夹有关:
 临时文件夹 --》 release --》 xx .exe文件
临时文件夹 --》 release --》 xx .exe文件
比如我的这个就是在D:\QtPro\build-Serial-Desktop_Qt_5_12_9_MinGW_64_bit-Release\release
把exe文件拷贝出来

随便在哪创建一个空的文件夹,然后将.exe文件拷贝进去
比如我在E盘新建了QTtest文件夹
三、使用命令终端添加程序所需的依赖库
在开始菜单中找到Qt命令终端(版本可能不一样打开对应版本就行),进入刚才新建的文件夹目录,使用 windeployqt 对生成的exe 文件进行打配置动态库文件:
一般来说,打开命令行终端后默认是在QT的安装路径下,这样需要先把路径切过去到exe文件的路径下再使用 windeployqt 命令 + .exe文件名操作

或者直接windeployqt + .exe文件绝对路径

这样就成功了,可以双击exe文件测试是否可以正常打开。
到这一步其实可以选择把整个文件夹打个压缩包,然后就可以发送到其他PC端使用了,只需解压缩即可。
如果还觉得麻烦,想只用一个exe文件就能独立工作,那就接着往下操作。
四、打包程序(下面的步骤只适用于Windows系统下)
(1) 安装Enigma virtual box工具
Enigma Virtual Box是软件虚拟化工具,它可以将多个文件封装到应用程序主文件,从而制作成为单执行文件的绿色软件。它支持所有类型的文件格式,虚拟化后的软件不释放任何临时文件到您的硬盘,文件模拟过程仅在内存运行。
Enigma virtual box官方链接:https://enigmaprotector.com/cn/downloads.html
进入官网后找到红框部分点击下载即可,不需要注册账号:
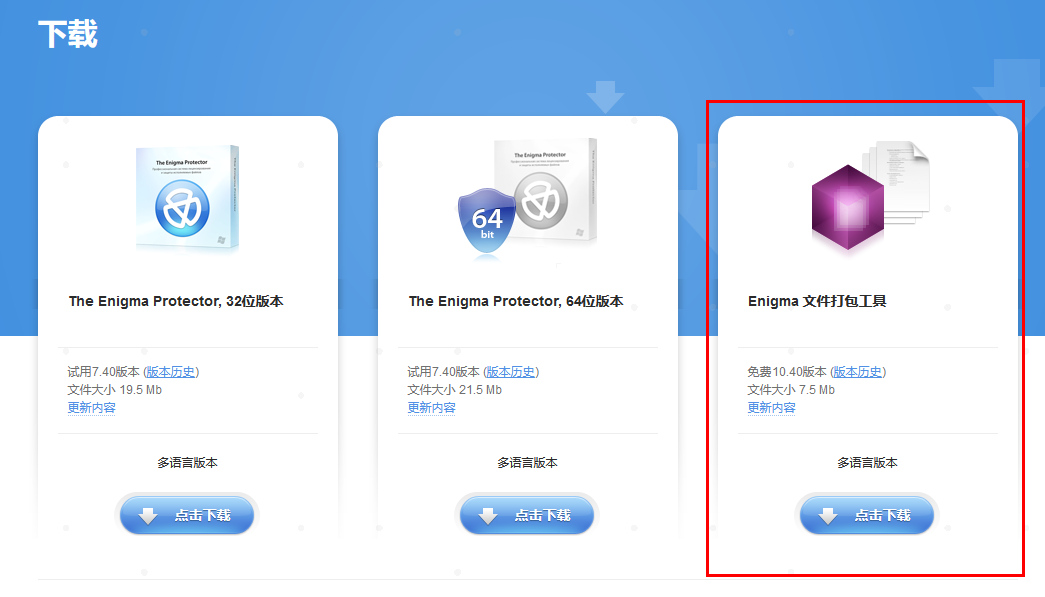
下载后点击安装,安装过程一直next就行,注意勾选创建桌面快捷方式,默认是不创建的。

安装好后:

打开还可以设置中文语言:
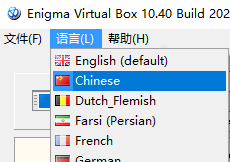
(2) 打开安装好的Enigma Virtual Box,点击浏览,找到第三步的目录下的exe文件:

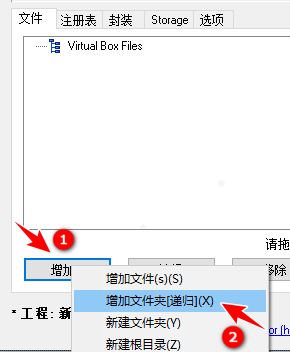
(3) 点击增加,选择递归添加文件,选中demo文件夹点击确定
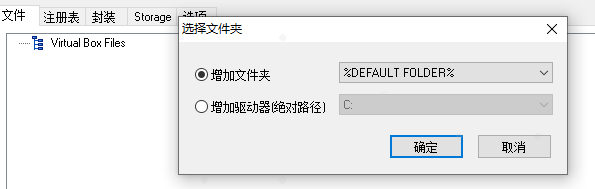
(4) 选择目标文件夹后点击确定
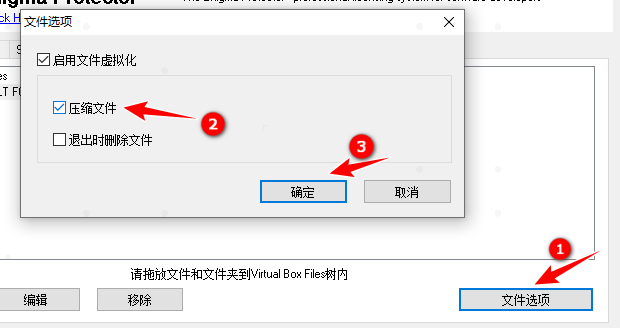
(5) 点击文件选项,选中压缩文件,点击确定
(6) 最后点击执行封包,等待结束即可。
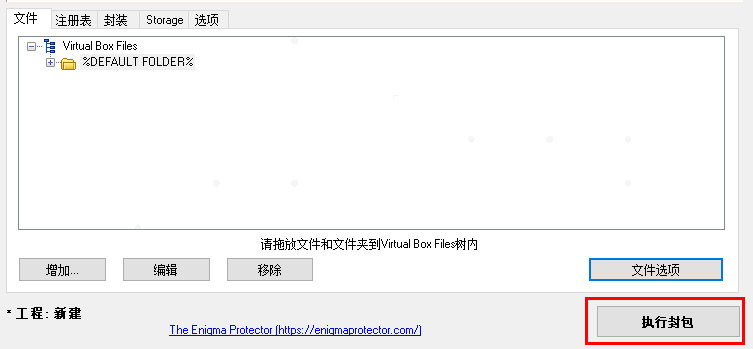
(7) 最终生成的文件名和路径,找到该文件双击打开测试是否正常
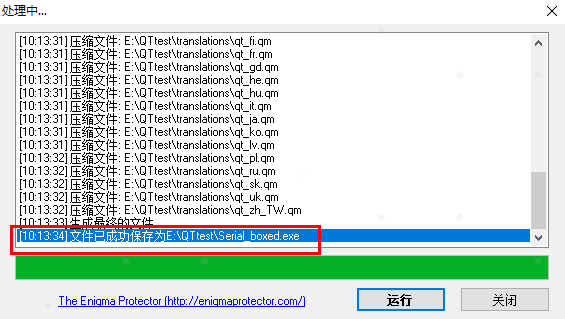
至此整个打包过程结束
推荐好文:
https://blog.csdn.net/childbor/article/details/125283893