一条单向的铁路线上,依次有编号为 1, 2, …, n的 n 个火车站。
每个火车站都有一个级别,最低为 1 级。
现有若干趟车次在这条线路上行驶,每一趟都满足如下要求:如果这趟车次停靠了火车站 xx,则始发站、终点站之间所有级别大于等于火车站 xx 的都必须停靠。(注意:起始站和终点站自然也算作事先已知需要停靠的站点)
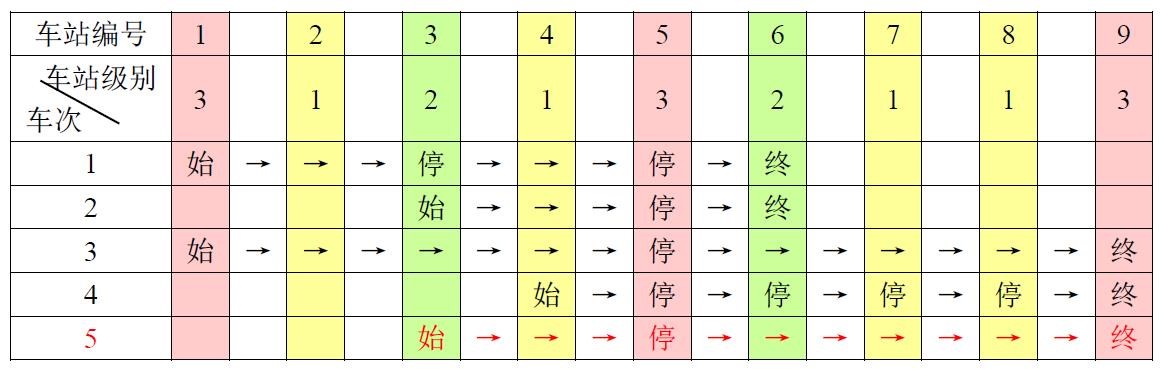
例如,下表是 5 趟车次的运行情况。
其中,前 4 趟车次均满足要求,而第 55 趟车次由于停靠了 3 号火车站(2 级)却未停靠途经的 6 号火车站(亦为 2 级)而不满足要求。
现有 mm 趟车次的运行情况(全部满足要求),试推算这 nn 个火车站至少分为几个不同的级别。
输入格式
第一行包含 2 个正整数 n,m,用一个空格隔开。
第 i+1行(1≤i≤m)中,首先是一个正整数 si(2≤si≤n),表示第 i趟车次有 si 个停靠站;接下来有 si 个正整数,表示所有停靠站的编号,从小到大排列。
每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。
输出格式
输出只有一行,包含一个正整数,即 nn 个火车站最少划分的级别数。
数据范围
1≤n,m≤1000
输入样例:
9 3
4 1 3 5 6
3 3 5 6
3 1 5 9
输出样例:
3【思路】
使用虚拟点,建立停靠站之间的关系。
【代码】
#include<bits/stdc++.h>
using namespace std;
const int N = 2010, M = 1e6 + 10;
int e[N], h[N], ne[N], d[N],dist[N];
int idx, st[N], n, m,w[N],q[N];
void add(int a, int b, int c)
{
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
d[b]++;
}
void topsort()
{
int hh = 0, tt = -1;
for (int i = 1; i <= n+m; i++)
{
if (!d[i])
q[++tt] = i;
}
while (hh <= tt)
{
int t = q[hh++];
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (--d[j] == 0)
{
q[++tt] = j;
}
}
}
}
int main()
{
cin >> n >> m;
memset(h, -1, sizeof h);
for (int i = 1; i <= m; i++)
{
memset(st, 0, sizeof(st));
int cnt;
cin >> cnt;
int start = n, endd = 1;//始发站和终点站
while (cnt--)
{
int stop;
cin >> stop;
start = min(start, stop);
endd= max(endd, stop);
st[stop] = 1;//停靠的点停靠过
}
int ver = n + i;//虚拟点
for (int j = start; j <= endd; j++)
{
if (!st[j])//没有停靠这个点
add(j, ver, 0);//从这个点到虚拟点连一条长度为0的边
else
add(ver, j, 1);//有级别关系,链接一条长度为1的边
}
}
topsort();
for (int i = 1; i <= n; i++)
dist[i] = 1;
for (int i = 0; i <n+m; i++)
{
int t = q[i];
for (int k = h[t]; k != -1; k = ne[k])
{
dist[e[k]] = max(dist[e[k]], dist[t]+w[k]);
}
}
int res = 0;
for (int i = 1; i <= n; i++)
res = max(res, dist[i]);
cout << res;
return 0;
}