作者：@小萌新
专栏：@算法
作者简介：大二学生 希望能和大家一起进步
本篇博客简介：介绍算法中的异或法

异或的概念

异或在书中一般是这么解释的

“ ^ ”的异或指的是二进制中 对应的对应二进制位相同时异或为零 相异时异或为一

但是我这里推荐一种很巧妙的记忆方式

异或就是二进制位无进位相加

我们下面使用一个例子来让大家更好的理解这句话

仔细观察 在上图中我们将对应位的二进制相加

• 如果有进位 则舍去进位
• 如果无进位 则不变

最后就得到了我们异或的结果

异或的两个性质

1. 0 ^ N = N
2. N ^ N = 0

我们一个个推导

首先来看性质一

0的所有二进制位都是0 而任何数加上0都不变 换一种说法也就是无进位 所以说该位不会改变

那么既然所有位都不会改变这个数当然也不会改变

其次是性质二

两个相同的数异或结果肯定为0

首先我们知道两个相同的数 每一位的二进制位肯定都相同 而二进制位一共就两种情况 0或1

• 如果是0 则两位相加之后还是0 不变
• 如果是1 则两位相加之后进位1 舍弃掉 所以说该位还是0

综上 我们就可以推出两个相同的数异或之后为0

最后根据这两个性质我们还能够推出一个重要的性质

如果一堆数字异或 那么无论我们怎么改变这堆数据的顺序 最后的结果都不会变

下面是简单的证明

首先不管是什么数字 它二进制的每个位肯定是确定的 不是0就是1

我们将每个位的所有数字累加起来只有两种结果 奇数还是偶数

我们上面说过 异或实际上就是无进位相加 如果是偶数模上2之后最后的结果会变成0 （进位都被我们舍弃了）

如果是技术模上2之后最后的结果会变成1 （进位都被我们舍弃了）

所以说 不管我们怎么改变顺序 每个位的数字都是不变的 所以说 如果一堆数字异或 那么无论我们怎么改变这堆数据的顺序 最后的结果都不会变

题目一 不使用额外变量交换两个数字

题目要求 不使用额外变量交换两个数字

交换两个数字的值最常用的方法就是申请一个临时变量 然后我们利用这个临时变量进行两个数字的交换

代码表示如下

  void swap(int& x , int& y)
  {
    int temp = x;
    x = y;
    y = temp;
  }

但是按照这个题目的意思 我们不能申请临时变量 这个temp是不允许使用的

这里我们可以使用算数的性质来解决这个问题

  void swap2(int& x , int& y)                                                                                  
  {                   
     x = x + y;
     y = x - y;
     x = x - y;
  }

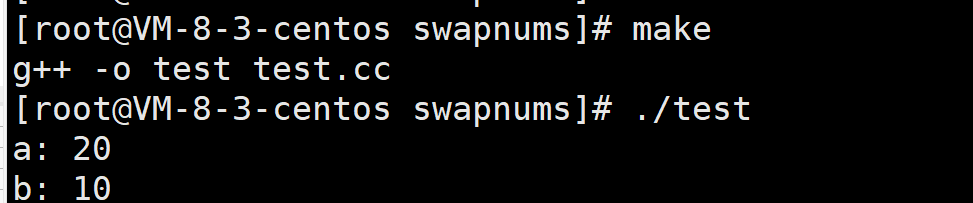
下面是运行的代码和结果

void swap2(int& x , int& y)    
{    
   x = x + y;    
   y = x - y;    
   x = x - y;    
}    
    
    
int main()    
{    
  int a = 10;    
  int b = 20;    
  swap2(a , b);    
    
  cout << "a: " << a << endl;    
  cout << "b: " << b << endl;                                                                                  
  return 0;    
} 

结果如下

但是这种解法有一种缺点 有可能会数据溢出

 x = x + y;   

如果此时我们的x和y特别大 超过了数据类型所能容纳的数字 就会造成数据溢出从而发生错误 所以说这种解法就是有缺陷的

此时为了防止数据溢出的情况我们就可以使用异或法来解决问题

代码和结果如下

void swap3(int& x , int& y)    
{    
  x = x ^ y;    
  y = x ^ y;    
  x = x ^ y;    
}    
    
int main()    
{    
  int a = 10;    
  int b = 20;    
  swap3(a , b);                                                                          
    
  cout << "a: " << a << endl;    
  cout << "b: " << b << endl;    
  return 0;    
}  

结果如下

同时我们的异或法只是改变数据的二进制位的情况 所以说数据绝对不会出现溢出

下面是原理解释 为什么进行三次异或就能够交换两个数的值

注意：

但是这里需要注意的是 如果A值和B值指向同一个空间 此时就不能使用异或法来交换两个值 因为异或之后两个数字百分百变为0

首先我们要知道 两个相同的数字异或是肯定为0的

我们上面进行了三次异或操作 每次异或操作之后只有一个数字变化了

但是如果两个值指向同一个空间 则进行一次异或操作之后该空间的值就会变为0 即两个数字都改变了

所以说使用该方法的时候千万要注意 两个值在计算机中不能使用同一空间

题目二 出现奇数次的数字

题目要求： 给你一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

该题目出现于lc136题 题目原文和测试用例如下

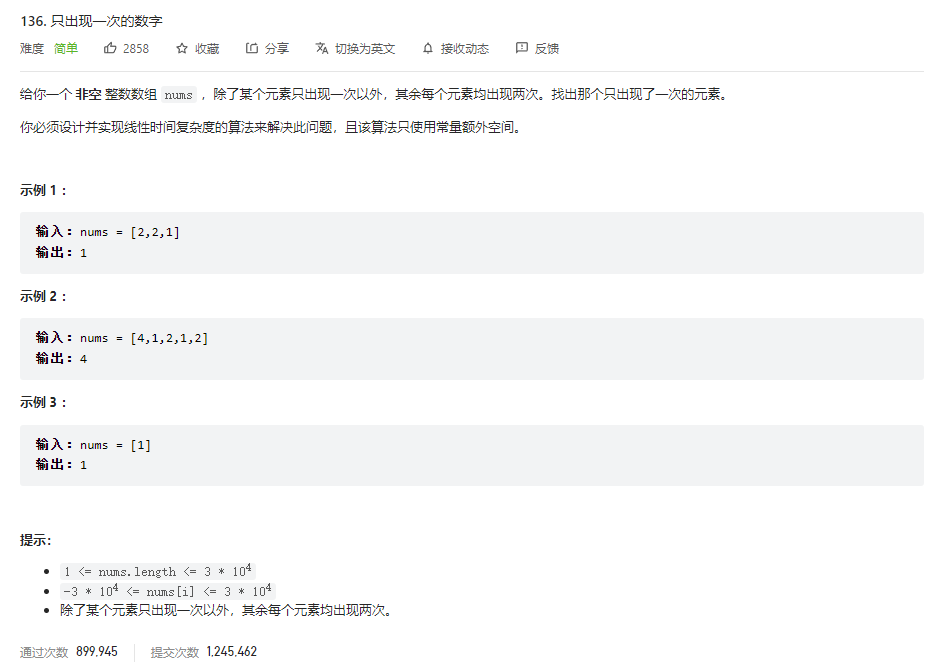
此时它要求我们找出一个数组中那个只出现一次的数字 我们第一时间就应该想到异或法

我们异或法是不是有一个性质

  N ^ N = 0

也就是说两个相同的数字异或 它们的值为0 当然我们也可以推广一下 偶数个相同的数字异或 它们的值为0

也就是说题目中所有出现偶数次的数字在异或之后都会变成0

然后根据异或法的第二个性质

  0 ^ N = N

我们最后那个出现一次的数异或上0 就能得到我们的最终结果了

代码表示如下

class Solution 
{
public:
    int singleNumber(vector<int>& nums) 
    {
        int eor = 0;
        for (auto x : nums)
        {
            eor ^= x;
        }

        return eor;
    }
};

运行结果如下

题目三 如何从一个整型数字中提取出右边的第一个1 （以整数类型表示）

当然遍历读取肯定是可以的

我们这里直接给出一个公式

  int a = 10;
  int rightone = a & (-a);

如果大家感兴趣可以自己推出下这个公式 （注意计算机中的原反补码）

因为10的二进制是 0000 1010 所以说rightone计算出的结果肯定是 0000 0010

如何计算一个32位无符号数中1的个数

该题我们可以使用我们上面学到的技巧 不断的提取该数字最右边的1

之后不断地将最右边的1消除就可以了 （取反异或）

代码和运行结果如下

class Solution {
public:
    int hammingWeight(uint32_t n) 
    {
        if (n == 0)
        {
            return 0;
        }

        int count = 0;
        while (n != 0)
        {
            size_t rightone = n & (-n);
            n &= ~rightone;
            count++;
        }

        return count;
    }
};

当然其实我们还有一种更巧妙的解法 我们这里直接给出代码

class Solution {
public:
    int hammingWeight(uint32_t n) 
    {
        if (n ==0)
        {
            return 0;
        }

        int count = 0;
        while( n &= (n - 1))
        {
            count++;
        }
        return ++count;
    }
};

这里其实就是运用了二进制的特性和位操作的特性 大家可以通过自己手动画图的方式来加深下了解

题目四 一个数组中两个数出现了一次 其他数出现了两次 如何找出这两个出现一次的数字

一个整型数组 nums 里除两个数字之外，其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n)，空间复杂度是O(1)。

这是lc上的剑指offer第56题 题目原文和测试用例如下

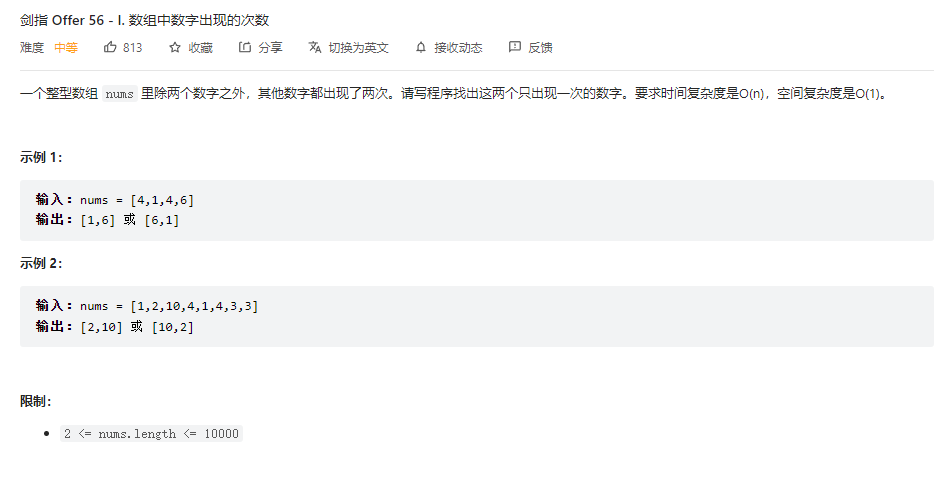
该题目其实和我们的题目二有些类似

我们通过异或之后能够将所有出现偶数次的数字变为0 最后的结果实际上就变为了两个出现一次的数字相互异或的结果

现在我们要想的就是如果通过该结果将该数组分为两部分 （因为这样子就变为了两个问题二 这样子就好解决多了）

根据异或的特性 异或之后的结果一定不为0 （特性2 两个相同的数字异或才为0 可以推出不同的数异或之后不为0 ） 所以说它们的二进制位上一定有为1的位

而这两个数在该二进制位上的位肯定是不同的 一个为0 一个为1 关于这一点 我们在前面已经推断过了

所以说我们就可以使用该二进制上是0还是1 将这两个数字分开 并且将整个数组分为两部分

并且我们可以保证在每一部分中只有一个数出现了一次 其他数都出现了两次 （两个相同的数二进制位肯定相同 所以说肯定出现在同一组中）

之后我们再重复题目二的解法就好了 代码和运行结果如下

class Solution {
public:
    vector<int> singleNumbers(vector<int>& nums) 
    {
        int eor = 0;
        for (auto x : nums)
        {
            eor ^= x;
        }

        int rightone = eor & (-eor); 
        

        int leftnum = eor; 
        for (auto x : nums)
        {
            if ((x & rightone) == 0)
            {
                leftnum ^= x; 
            }
        }
        int rightnum = eor ^ leftnum;

        vector<int> ans;
        ans.push_back(leftnum);
        ans.push_back(rightnum);

        return ans;
    }
};

运行结果如下

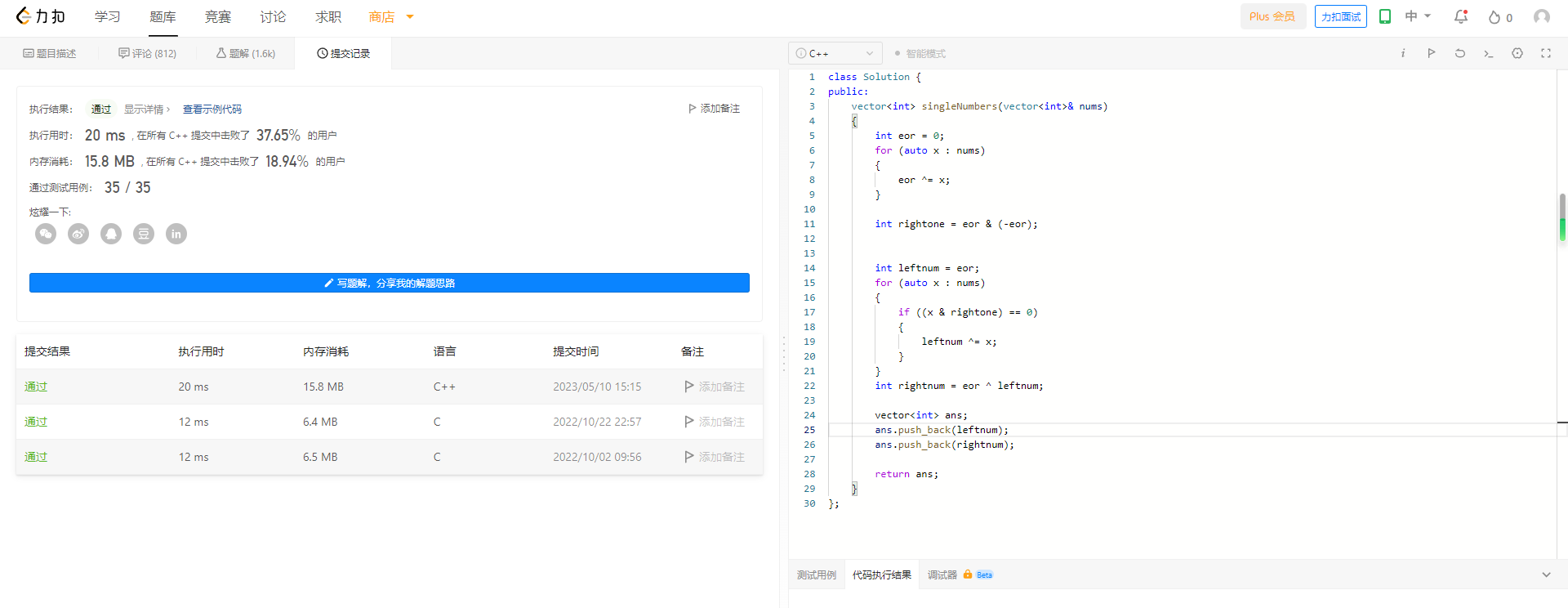
题目五 一个数组中一个数出现了一次 其他数出现了三次 要求你找出出现一次的这个数

在一个数组 nums 中除一个数字只出现一次之外，其他数字都出现了三次。请找出那个只出现一次的数字。

这是lc上剑指offer的第56题二 题目原文和测试用例如下

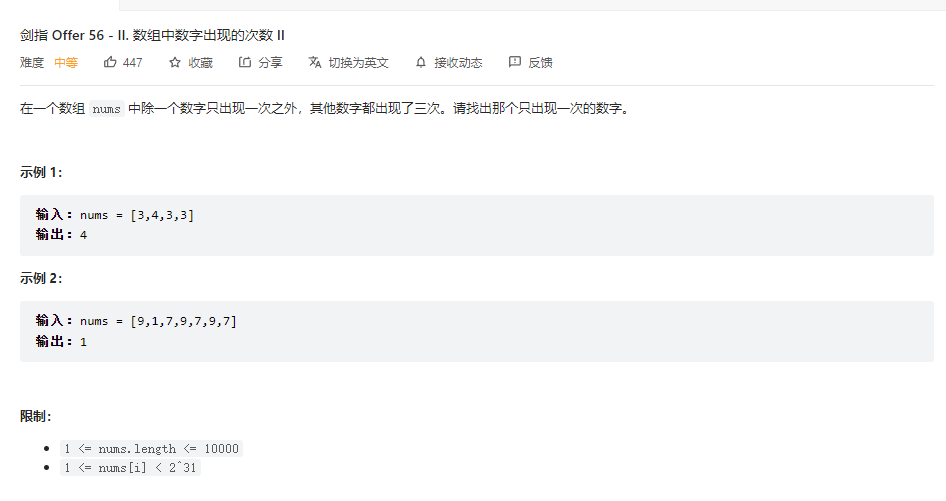
这道题其实就有点超出异或的范畴了 不过出现在异或法的同源题目上我们就讲解下

我们首先假设 所有的数字都出现了三次 那么在比特位上会是什么情况呢？

是不是所有的比特位都能够被3整除啊

那么我们现在转化下思路 加上那个只出现一次的数字

是不是就说明不能被3整除的比特位就肯定是那个数字出现的地方

那么我们遍历32个比特位 看哪些位不能被3整除 是不是就能够找出那个只出现一次的数字啊

其实这个题目还能做延申 如果一个数字出现 M 次 （1 < M < K ） 其余数字都出现 K次 我们找出这个出现M次数字的方式和这道题的解法是一模一样的

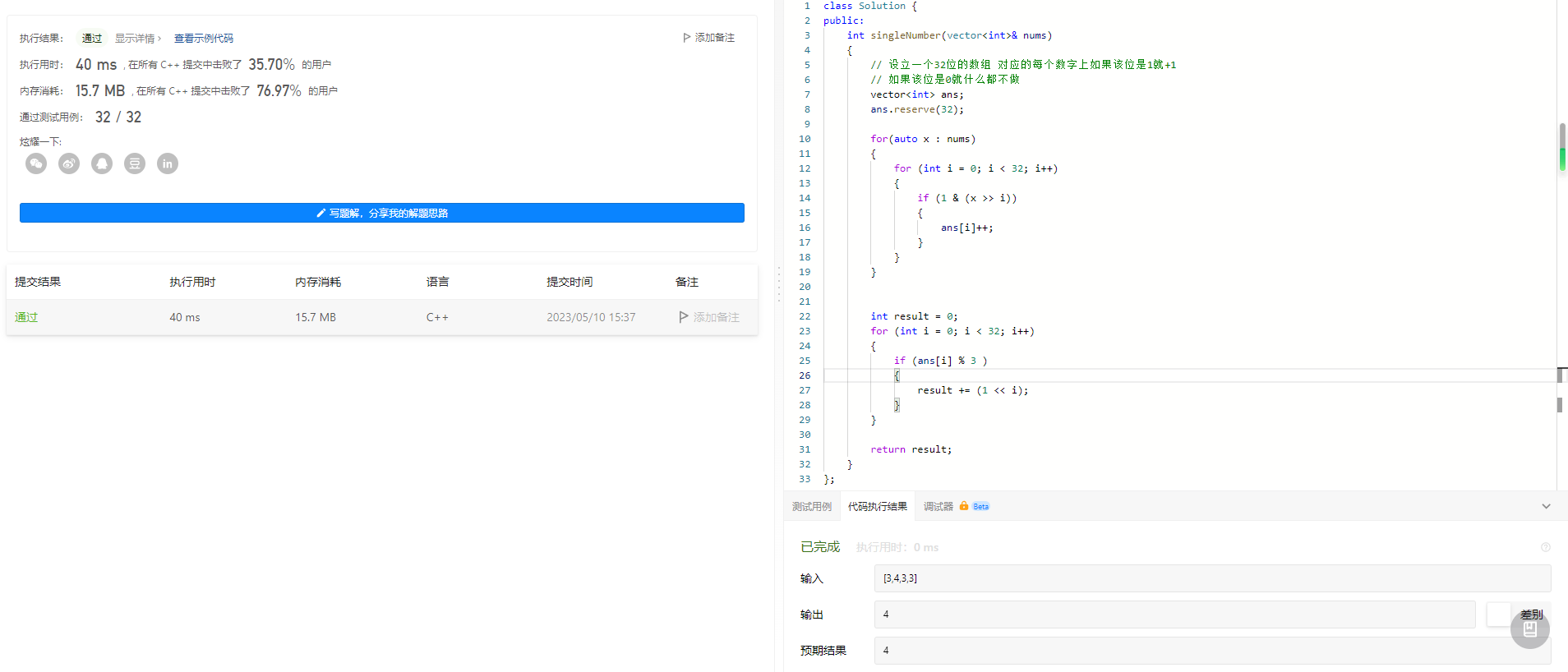
代码和演示结果如下

class Solution {
public:
    int singleNumber(vector<int>& nums) 
    {
        // 设立一个32位的数组 对应的每个数字上如果该位是1就+1
        // 如果该位是0就什么都不做 
        vector<int> ans;
        ans.reserve(32);

        for(auto x : nums)
        {
            for (int i = 0; i < 32; i++)
            {
                if (1 & (x >> i))
                {
                    ans[i]++;
                }
            }
        }


        int result = 0;
        for (int i = 0; i < 32; i++)
        {
            if (ans[i] % 3 )
            {
                result += (1 << i);
            }
        }

        return result;
    }
};