PS：本文有一定阅读门槛，如果有不明白的地方欢迎评论询问！

1 模型概述

接下来我们将要学习我们的第一个模型——线性回归。比如说我需要根据数据预测某个面积的房子可以卖多少钱

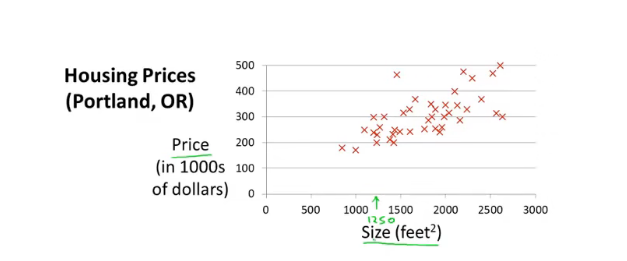
接下来我们会用到以下符号：

• m:训练样本数量
• x:输入值，又称为属性值
• y:输出值，是我们需要的结果

我们会用$(x,y)$表示一整个训练样本，使用$(x^{(i)},y^{(i)})$来表示第i个样例
我们将上图用表格表示出来如下：

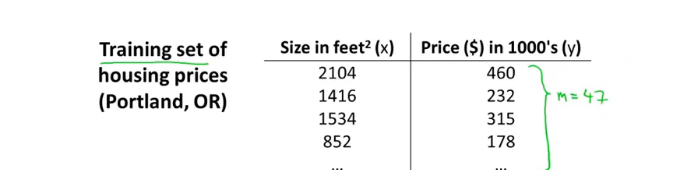
那么线性回归的预测模型如下：

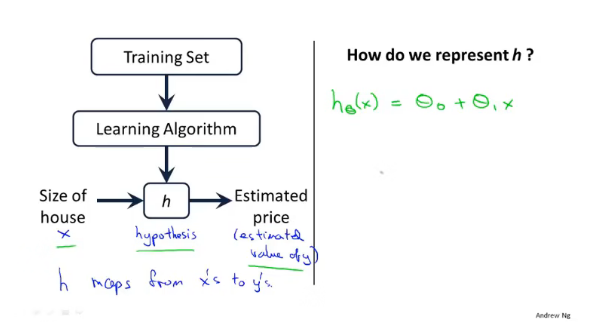
训练集输入到学习算法中，然后学习算法会根据数据训练出函数h。作为一个线性回归模型，其输出的h应该是$h(x)={\theta }_0+{\theta }_{1}x$，图像为一条直线。得到函数h后，我们只需要输入房屋的大小，就可以得到估算的价格

2 代价函数

以上面的$h(x)={\theta }_0+{\theta }_{1}x$为例子，不同的${\theta }_0$和不同的${\theta }_1$会得出不同的假设函数，我们需要做的是选择出恰当的值，使得假设函数和数据集中的点更好地拟合，也就是说对于样本$(x_i,y_i)$，值$|h(x_i)-y_i|$越小越好，进一步精确地定义我们要解决的问题就是，在让${\theta }_0$和${\theta }_1$尽量小的情况下，$|h(x_i)-y_i|$越小越好，这是一个最小化问题。

那么我们用以下式子衡量假设函数的优劣：
$$J=\frac{1}{2m}\sum _{i=1}^m{h}_{\theta }(x^{(i)}-y^{(i)}{)}^2$$
其中i表示的是第i个样例 ，总共有m个样例，这就是线性回归的代价函数，这个函数的值越小越好，接下来我们会详细剖析代价函数

我们先只考虑$h(x)={\theta }_{1}x$的情况，也就是${\theta }_1=0$，那么如果数据集为(1,1)，(2,2)，(3,3)，那么以${\theta }_1$为横坐标，以$J({\theta }_1)$为纵坐标，可以画出如下图像

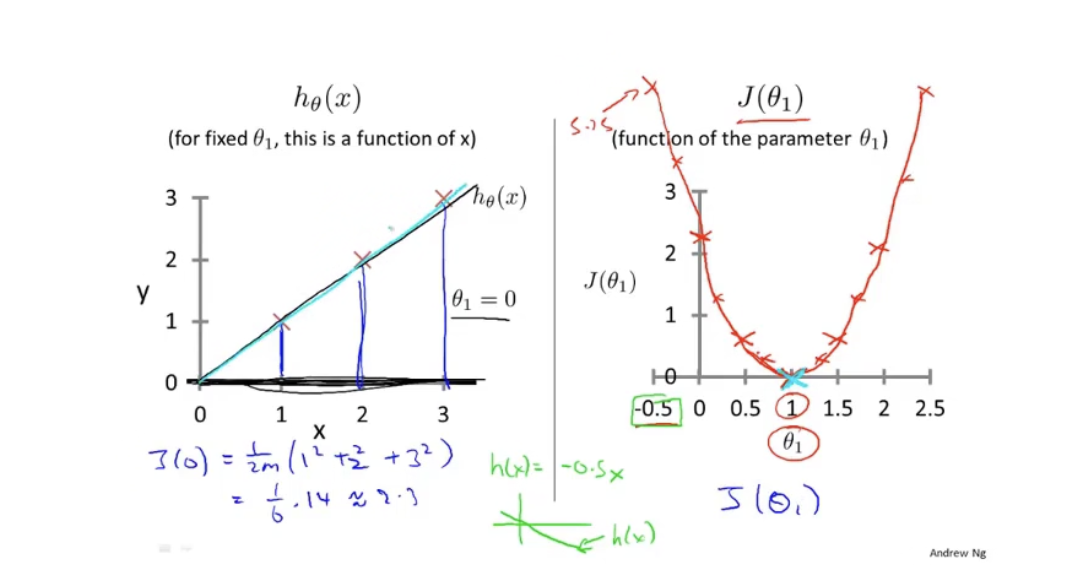
可以看出${\theta }_1=1$的时候$J({\theta }_1)$最小

当我们同时考虑${\theta }_1$和${\theta }_0$的时候，得到的代价函数则是一个类似于等高线图的三维图像

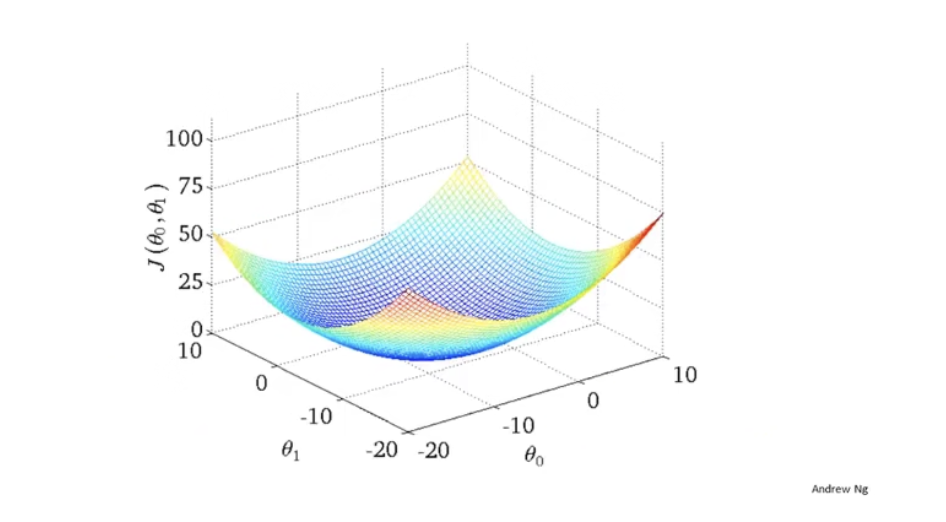
当然，我们也可以使用等高线标出：

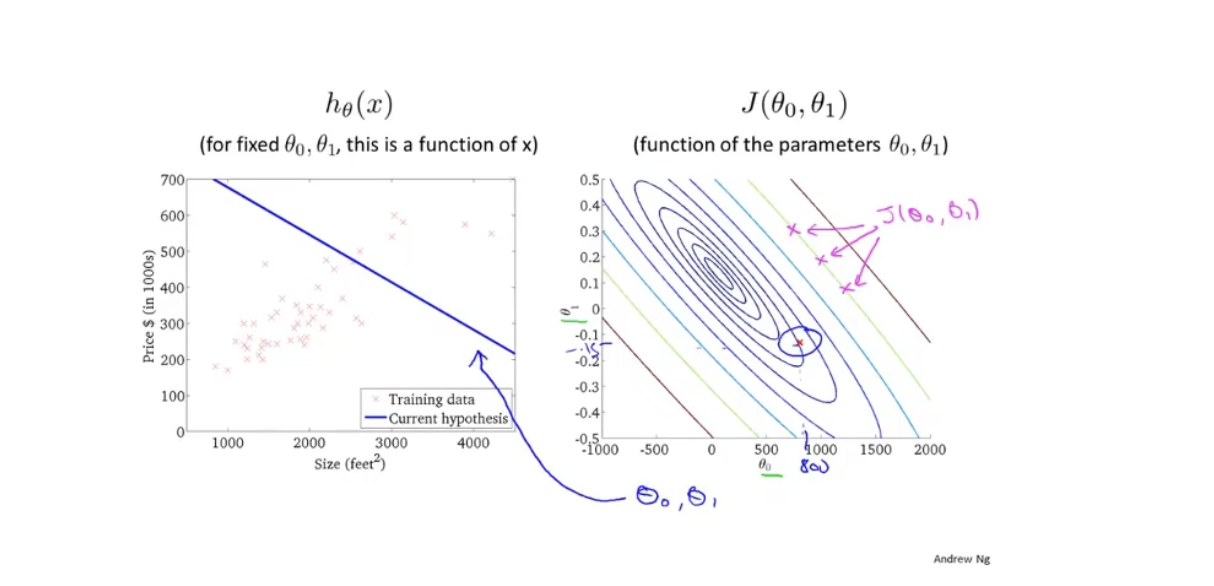
在图中，圆心部分是J值最小的部分，也就是拟合得最好的${\theta }_1$和${\theta }_0$的取值，我们知道了J的图像之后，那么我们编写的算法的目标就是如何找到J的最小值

3 梯度下降

梯度下降是十分常用的算法，不仅仅是线性回归，其他机器学习算法中也会频繁用到。

假设我们现在有一个函数$J({\theta }_0,{\theta }_1)$(不一定是线性回归的代价函数)，需要找出其最小值$minJ({\theta }_0,{\theta }_1)$

首先我们给${\theta }_0$和${\theta }_1$赋予初值，通常都是0，梯度下降需要做的事情就是不断微调两个值，从而找出J的最小值或者局部最小值。假设函数J图像如下：

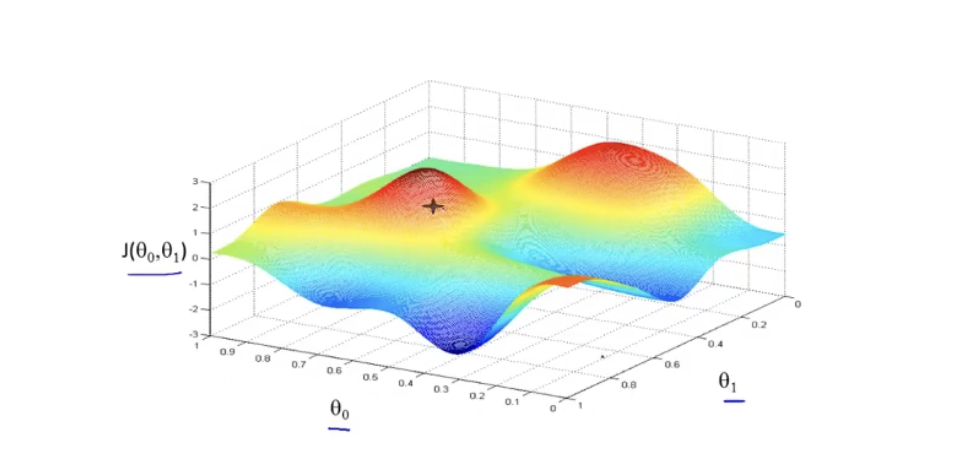
我们可以将图像想象成两个山，并且点站在了红色的山顶上，梯度下降就是环顾四周，看看哪个方向下山是最快的，也可以理解为斜率最大的方向。然后试探着迈出一步后，再重复上述步骤，直到找到一个地方，四周围的点集都要比该点高，那么这就是一个局部最优解或最优解，示例如下图

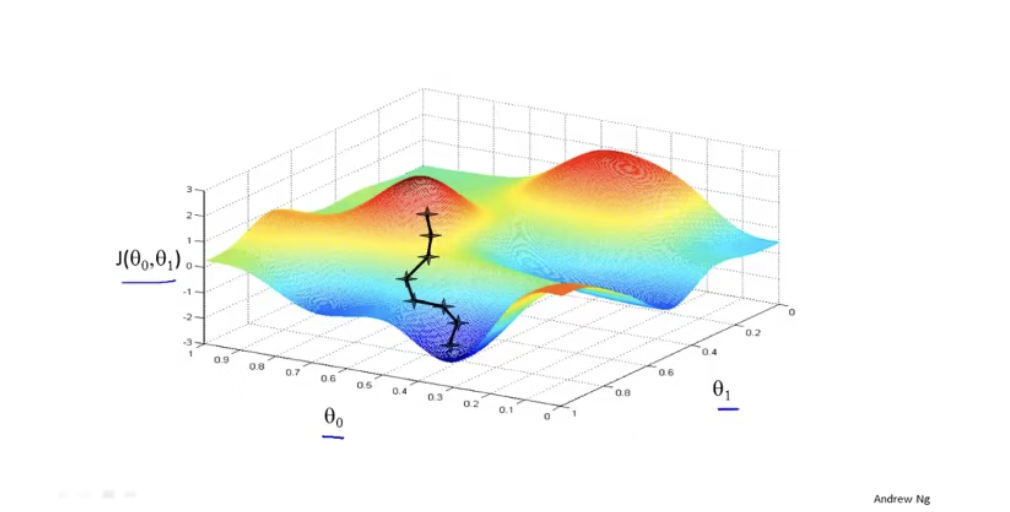
这很像算法课里的贪心思想是不是！既然是贪心，那么得到的就可能不是最优解，比如下面的例子：

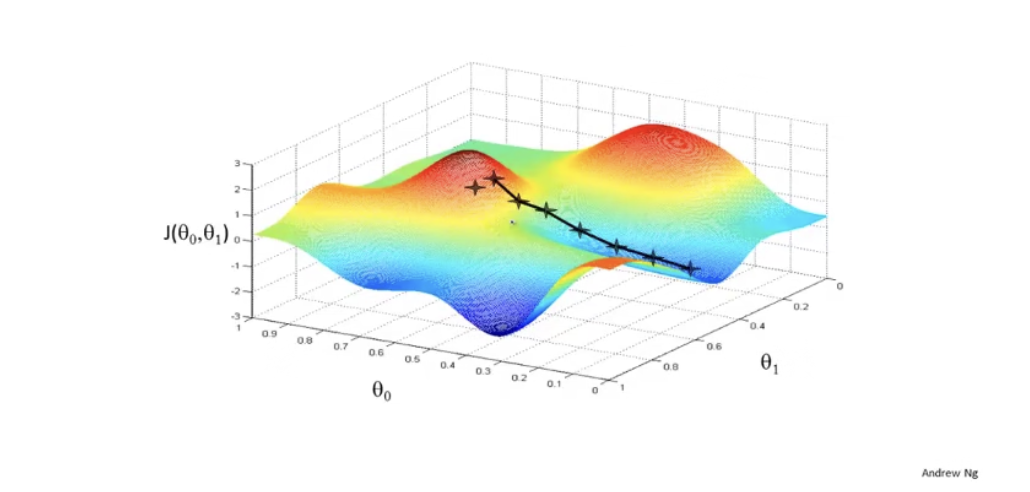
如果我们更改一下起始点，那么按照上述的方法可能到达的地方就并非是J的最优解，而只是一个局部最优解。我们也可以看到，更改起始点会得到不同的局部最优解

梯度下降的数学定义如下：

我们会反复做这一步，直到收敛。其中:=为赋值运算符，$\alpha$表示学习率，用来控制梯度下降时我们迈的步子有多大，以后会细讲。后面的$\frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1)$则是一个导数，后面的则是指明了更新的条件，当j=0或者j=1的时候更新 ，更新的时候需要同时更新${\theta }_0$和${\theta }_1$。下面的Simultaneous update表明了其更新的过程，首先经值暂存于temp0和temp1中，然后将这两个值依次赋予${\theta }_0$和${\theta }_1$

假设我们的最小化参数只有${\theta }_1$，并且$J({\theta }_0)$的曲线如下：

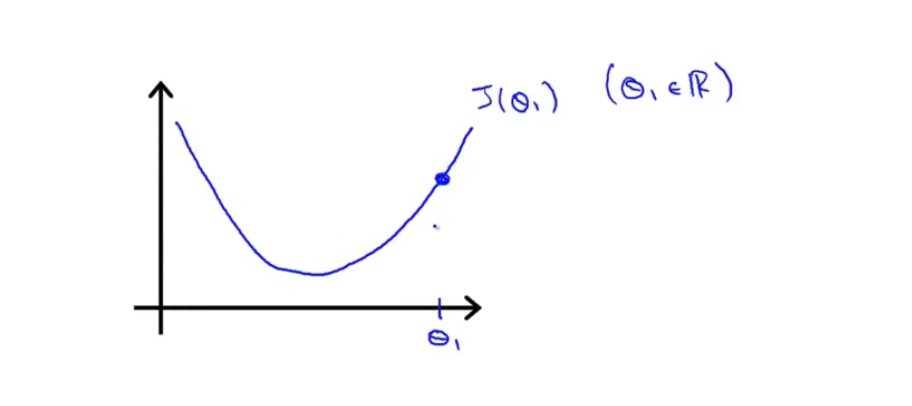
如果我们从${\theta }_1$处开始梯度下降，那么梯度下降要做的就是不断地更新${\theta }_1:={\theta }_1-\frac{\partial }{\partial {\theta }_1}J({\theta }_1)$，可以看出，这是一个递归的过程。仔细看这个公式，其中$\frac{\partial }{\partial {\theta }_1}J({\theta }_1)$是当前${\theta }_1$所在位置的导数，也可以简单理解为点$({\theta }_1,J({\theta }_1))$的斜率，那么如果$\alpha$越大，${\theta }_1$变化得也越快。以上图为例子，其${\theta }_1$所在位置的导数为正数，那么${\theta }_1$会减小；如果${\theta }_1$所在位置的导数为负数（比如下图的情况），那么${\theta }_1$会逐渐增大

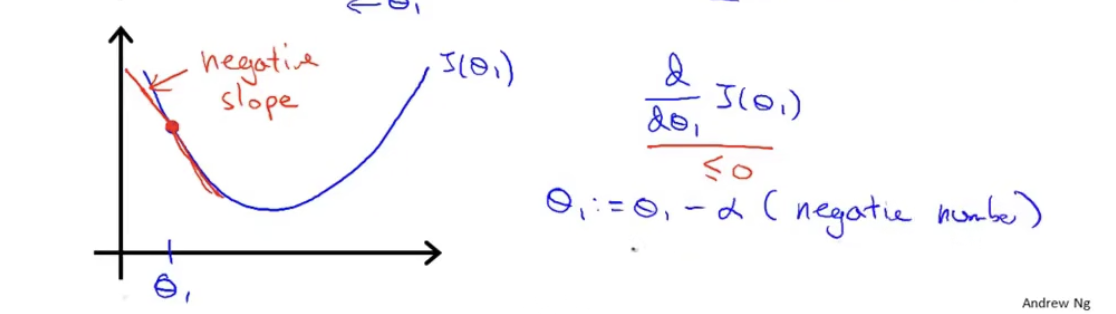
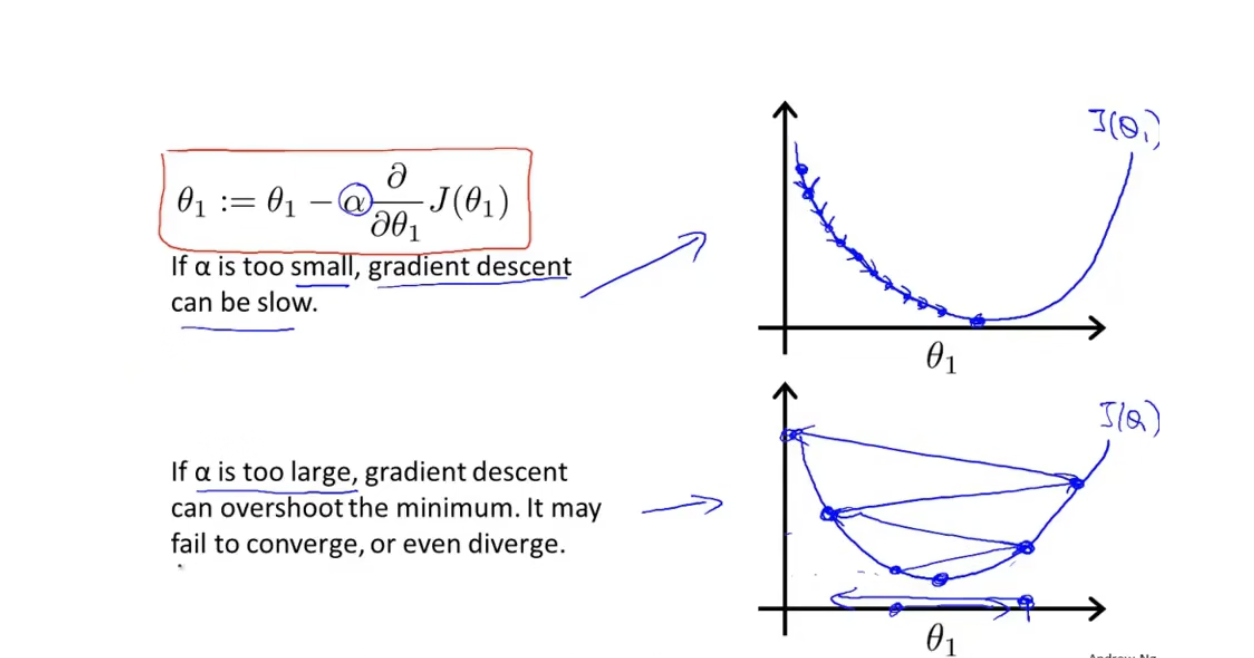
上述两个例子说明，无论是什么情况，他都会趋向于走向J值更小的位置，如果已经到达了J值最小的位置，那么该位置的导数$\frac{\partial }{\partial {\theta }_1}J({\theta }_1)=0$，此时的${\theta }_1:={\theta }_1-\frac{\partial }{\partial {\theta }_1}J({\theta }_1)$就不会发生变化，另外，当${\theta }_1$靠近最优解的时候，由于导数逐渐变小，其每次迈出的步子也越来越小。对于$\alpha$值，如果学习速率太小，那么他需要很多次递归才能到达最低点；如果学习速率太大，那他会很有可能越过最低点，甚至会导致无法收敛或者直接就发散了。

当然，在这个图像里只有一个局部最优解，这个局部最优解就是整体最优解，如果我们换一个图像会怎么样。

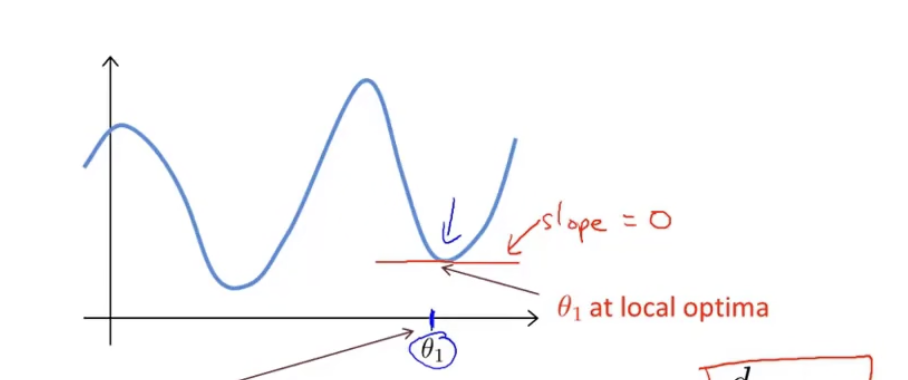
如果是上述图像，也许我们到达了${\theta }_1$的位置，这个位置是一个局部最优点，但是他并非是全局的最优解

将上面的过程推广开来，假设函数为$J({\theta }_1,{\theta }_2,{\theta }_3....{\theta }_n)$，也可以应用梯度下降求出其最小值

4 线性回归中的梯度下降

本节将会用梯度函数和代价函数相结合，得到线性回归的算法，这可以用直线拟合数据。我们上文说到，线性回归的模型函数是$$J=\frac{1}{2m}\sum _{i=1}^m{h}_{\theta }(x^{(i)}-y^{(i)}{)}^2$$然后其梯度下降的函数为
$${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1)$$将两者合并后可得出$$\alpha \frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1)=\alpha \frac{\partial }{\partial {\theta }_j}\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$
又因为函数$h_{\theta }(x^{(i)})={\theta }_0+{\theta }_1{x}^{(i)}$，所以
$$\alpha \frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1)=\alpha \frac{\partial }{\partial {\theta }_j}\frac{1}{2m}\sum _{i=1}^m({\theta }_0+{\theta }_1{x}^{(i)}-y^{(i)}{)}^2$$接着我们就计算导数$$\frac{\partial (\frac{1}{2m}{\sum }_{i=1}^m({\theta }_0+{\theta }_1{x}^{(i)}-y^{(i)}{)}^2)}{\partial {\theta }_j}$$如果是对${\theta }_0$求偏导可以得出$$\frac{\partial }{\partial {\theta }_0}J({\theta }_0,{\theta }_1)=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})$$对${\theta }_1$求偏导可得$$\frac{\partial }{\partial {\theta }_1}J({\theta }_0,{\theta }_1)=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\ast x(i)$$综上所述，可以知道最终${\theta }_0$和${\theta }_1$的计算公式为
$${\theta }_0:={\theta }_0-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})$$$${\theta }_1:={\theta }_1-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\ast x^{(i)}$$

还有一个问题就是，我们知道，代价函数可能会有数个局部最优解，梯度下降的起始点会使得梯度下降的结果导向不同的局部最优解。如下图所示

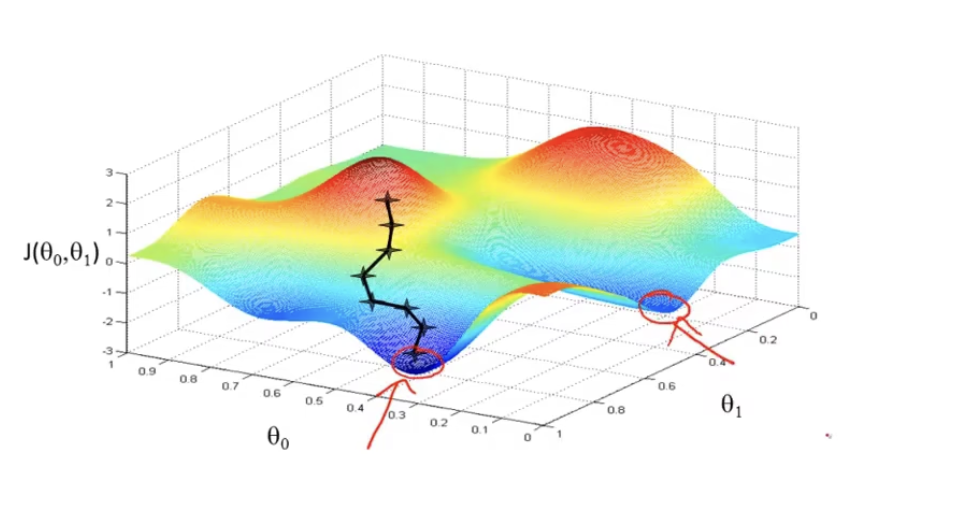
但是实际上我们在线性回归中并不需要考虑这个问题，因为线性回归的代价函数总是一个弓形函数，它只有一个全局最优。

当你使用线性回归计算这种代价函数的梯度下降，他总会收敛到全局最优，因为他只有一个最优解

上面介绍的算法又称为Batch梯度下降算法，其含义是梯度下降的每一步都会考虑整个数据集的数据。与之相对的是，某些算法在进行梯度下降时会只考虑数据集中的部分子集，比如说和当前点相关性较大的数据