目录

一.排序

1.概念

1.1排序

1.2稳定性

2.七大基于比较的排序

二.插入排序

3.1 直接插入排序-原理

2.折半插入排序

3.分析

二.每日一题订正

1.选择题

2.不要二

三.希尔排序

1 原理

2.代码实现

3.分析

四.选择排序

1.原理

2.代码

3.优化版

4.分析

五.测量时间的方法

---

一.排序

1.概念

1.1排序

排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。

平时的上下文中，如果提到排序，通常指的是排升序（非降序）。

通常意义上的排序，都是指的原地排序(in place sort)

1.2稳定性

两个相等的数据，如果经过排序后，排序算法能保证其相对位置不发生变化，则我们称该算法是具备稳定性的排序算

法。

2.七大基于比较的排序

最常见的排序方法:快速排序,堆排序,归并排序

二.插入排序

3.1 直接插入排序-原理

整个区间被分为

1. 有序区间
2. 无序区间

每次选择无序区间的第一个元素，在有序区间内选择合适的位置插入

定义一个J 为i-1 把i的值放在一个tmp的变量.

如果j的值大于tmp,就把j的值放到j+1的位置 并且j会退.再次比较j的值与tmp的大小.直到回推到负数的位置上,就跳出了

就说明tmp是最小的那个但是进不出循环所以需要再外写一个

如果小于,就j+1直接等于tmp,这里j就不需要再会退了因为前面都是有序的所以直接跳出循环

public static void directSort(int[] array){
    for (int i = 1; i < array.length; i++) {
        int tmp=array[i];
        int j = i-1;
        for (; j>=0 ; j--) {
           if(array[j]>tmp){
               array[j+1]=array[j];
           }else{
              // array[j+1]=tmp;
               break;
           }
        }
        array[j+1]=tmp;
    }
}

2.折半插入排序

如果将一个无序的树插入到以一个有序的数组,就在二分查找比这个数大的数然后插入

public static void bsInsertSort(int[] array) {
  for (int i = 1; i < array.length; i++) {
    int v = array[i];
    int left = 0;
    int right = i;
    // [left, right)
    // 需要考虑稳定性
    while (left < right) {
      int m = (left + right) / 2;
      if (v >= array[m]) {
        left = m + 1;
     } else {
        right = m;
     }
   }
    // 搬移
    for (int j = i; j > left; j--) {
      array[j] = array[j - 1];
   }
    array[left] = v;
 }
}

3.分析

/**
 * 直接插入排序
 */
/**
 * 时间复杂度：O(N^2) 。逆序的时候
 *      最好的情况是O(N): 对于直接插入排序来说，最好的情况就是数据有序的时候
 *      根据这个结论，推导出另一个结论：对于直接插入排序来说，数据越有序，越快。
 *
 * 空间复杂度：O(1)
 * 稳定性：稳定的
 *
 * 一个稳定的排序，可以实现为不稳定的排序
 * 但是一个本身就不稳定的排序，是不可以变成稳定的排序的
 * 经常使用在  数据量不多   且 整体数据 趋于有序了
 * @param array
 */对数据敏感

二.每日一题订正

1.选择题

abstract不能和final同时出现,因为abstract是要被重写的

D选项也可以通过super或者this调用

A选项是八进制

2.不要二

欧几里得举例可以表示为2的平方

也就是

不能等于4

我们举例a2+b2等于4的情况并且ab都要为正整数

所以只有可能是 0 4

4 0

也就是横坐标相同.纵坐标多2

或者是纵坐标相同.横坐标多2

/**
 * 希尔排序
 * @param
 */
public static void shellSort(int[] arr){
    int gap=arr.length;
    while(gap>0){
        gap/=2;
        shell(arr,gap);
    }
}
public static void shell(int[]arr,int gap){
    for (int i = 1; i < arr.length; i++) {
        int tmp=arr[i];
        int j=i-gap;
        for (; j>=0 ; j-=gap) {
            if(arr[j]>tmp){
              arr[j+gap]=arr[j];
            }else{
                break;
            }
        }
        arr[j+gap]=tmp;
    }
}

三.希尔排序

1 原理

希尔排序法又称缩小增量法。希尔排序法的基本思想是：先选定一个整数，把待排序文件中所有记录分成个组，所有

距离为的记录分在同一组内，并对每一组内的记录进行排序。然后，取，重复上述分组和排序的工作。当到达=1时，

所有记录在统一组内排好序。

1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的对比

2.代码实现

public static void selectSort(int[] arr){
    for (int i = 0; i < arr.length; i++) {
        for (int j = i+1; j < arr.length ; j++) {
            if(arr[j]<arr[i]){
                int tmp=arr[i];
                arr[i]=arr[j];
                arr[j]=tmp;
            }
        }
    }
}

3.分析

/**
 * 其实就是一个直接插入排序
 * @param array 待排序序列
 * @param gap 组数
 */
/**
 * 时间复杂度[和增量有关系的]：O(n^1.3 - n^1.5)
 * 空间复杂度：O(1)
 * 稳定性：不稳定的
 *   看在比较的过程当中  是否发生了跳跃式的交换 如果发生了跳跃式的交换  那么就是不稳定的排序
 * 基本上没有考过
 * @param array
 */对数据不敏感

四.选择排序

1.原理

每一次从无序区间选出最大（或最小）的一个元素，存放在无序区间的最后（或最前），直到全部待排序的数据元素排完

定义两个指针,让i从0下标开始.j从i+1开始往后遍历遇到比i大的就根i所在的值进行交换

2.代码

public static void selectSort(int[] arr){
    for (int i = 0; i < arr.length; i++) {
        for (int j = i+1; j < arr.length ; j++) {
            if(arr[j]<arr[i]){
                int tmp=arr[i];
                arr[i]=arr[j];
                arr[j]=tmp;
            }
        }
    }
}

3.优化版

j从后遍历的时候,先定义一个最小值等于i下标的值.如果j找到比min小,就更新min的值等于当前j下标的值

等循环结束,再交换

public static void selectSort1(int[] arr){
    for (int i = 0; i < arr.length; i++) {
        int min=i;
        for (int j=i+1; j < arr.length ; j++) {
            if(arr[j]<arr[min]){
                min=j;
            }
        }
        int tmp=arr[i];
        arr[i]=arr[min];
        arr[min]=tmp;
    }
}

4.分析

* 选择排序
* 时间复杂度：O(N^2)
*
* 时间复杂度 != 代码的运行时间
*
* 其实 不是看你运行的时间 来说明的 时间只是一个衡量的某个标准
* 空间复杂度：O(1)
* 稳定性：不稳定的排序
* @param array 待排序序列
*/

数据敏感:意思就是有序无序时间都差不多.

五.测量时间的方法

用当前时间方法

system.currenttimemills

用无序的就用随机数公式

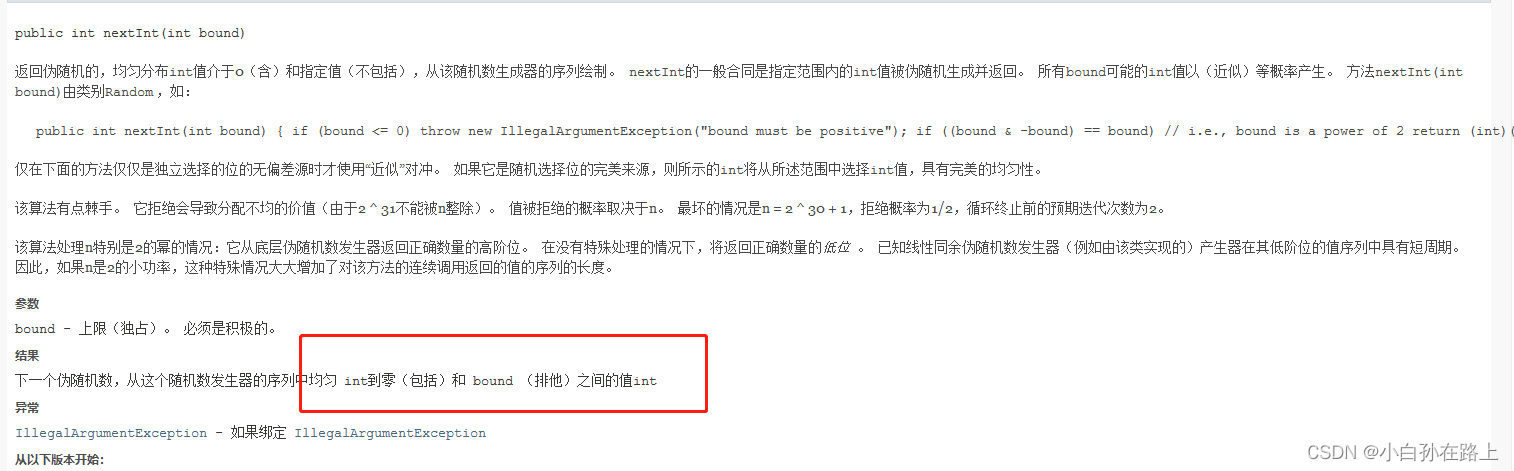
public static void test1(int capacity) {
    int[] array = new int[capacity];
    for (int i = 0; i < array.length; i++) {
        array[i] = i;
    }
    long start = System.currentTimeMillis();
    //directSort(array);
   // shellSort(array);
    selectSort(array);
    //heapSort(array);
    //quickSort(array);
    long end = System.currentTimeMillis();
    System.out.println(end-start);
}

/**
 * 无序的数据
 * @param args
 */
public static void test2(int capacity) {
    int[] array=new int[capacity];
    Random random=new Random();
    for (int i = 0; i < capacity; i++) {
        array[i]=random.nextInt(capacity);//
    }
    long start = System.currentTimeMillis();
   // directSort(array);
 // shellSort(array);
    selectSort(array);
    //heapSort(array);
    //quickSort(array);
    long end = System.currentTimeMillis();
    System.out.println(end-start);

}

public static void main(String[] args) {
    test1(10_0000);
    test2(10_0000);
}