文章目录
- A. Love Story(模拟)
- B. Blank Space(模拟)
- C. Mr. Perfectly Fine(模拟)
- D. Gold Rush(小思维)
- E. The Lakes(DFS)
- F. Forever Winter(简单的图)
- G. Hits Different(二维前缀和)
- H. Don't Blame Me(状态压缩dp)
传送门
A. Love Story(模拟)
题意:比较字符串
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define eps 1e-9
using namespace std;
const int N = 105;
string o = "codeforces";
void solve() {
string s;
cin >> s;
int cnt = 0;
for (int i = 0; i < 10; i++) if (s[i] != o[i]) cnt++;
cout << cnt << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
int T = 1;
cin >> T;
while (T--) {
solve();
}
return 0;
}
B. Blank Space(模拟)
题意:求出最长连续的0,典中典
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define eps 1e-9
using namespace std;
const int N = 105;
int a[N];
void solve() {
int n;
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
int cnt = 0, ans = 0;
for (int i = 1; i <= n; i++) {
if (!a[i]) cnt++;
else ans = max(cnt, ans), cnt = 0;
}
ans = max(cnt, ans);//注意这个
cout << ans << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
int T = 1;
cin >> T;
while (T--) {
solve();
}
return 0;
}
C. Mr. Perfectly Fine(模拟)
题意:给出花费和01串,让你找到,这些串异或和为11的最小花费。
思路:00是无用书,只需求出01 10 11的最小花费,如果没有11而且,01 10缺一个就是做不到,其余两种求最小即可。
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define eps 1e-9
using namespace std;
const int N = 105;
void solve() {
int a = inf, b = inf, c = inf;
int n;
cin >> n;
for (int i = 0; i < n; i++) {
int x;
cin >> x;
string s;
cin >> s;
if (s == "00") continue;
if (s == "10") a = min(a, x);
if (s == "01") b = min(b, x);
if (s == "11") c = min(c, x);
}
if (c == inf && (a == inf || b == inf)) {
cout << -1 << '\n';
return;
}
cout << min(a + b, c) << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
int T = 1;
cin >> T;
while (T--) {
solve();
}
return 0;
}
D. Gold Rush(小思维)
题意:给你两个整数m,n,你每次可以把一个数拆成两份,大份的恰好是小份两倍,你可以在产生的新的数继续这样操作,问你是否能够从m中拆出n。
思路:我们可以知道 n/m= 1/3 * 2/3.。。。的乘积,因为每次都是取大份,或者取小份。化简分式后,统计分母是不是只有3,分子是不是只有2,而且2的数目小于3的数目即可。
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define eps 1e-9
using namespace std;
const int N = 105;
void solve() {
int n, m;
cin >> n >> m;
int gcd = __gcd(n, m);
n /= gcd, m /= gcd;
int cnt1 = 0, cnt2 = 0;
while (n % 3 == 0) n /= 3, cnt1++;
while (m % 2 == 0) m /= 2, cnt2++;
if (n == 1 && m == 1 && cnt1 >= cnt2) {
cout << "YES\n";
} else cout << "NO\n";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
int T = 1;
cin >> T;
while (T--) {
solve();
}
return 0;
}
E. The Lakes(DFS)
题意:给你一个非负矩阵,让你求出最大的正数联通块的权值和。
思路:标准的DFS,思路一定要清晰,主要起始点能否开始,出发出的标记一定要打好。
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define eps 1e-9
using namespace std;
const int N = 1005;
int mp[N][N], vis[N][N], n, m;
int cnt, go[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};//方向数组
void dfs(int x, int y) {
for (int i = 0; i < 4; i++) {
int nx = x + go[i][0], ny = y + go[i][1];
if (nx < 1 || nx > n || ny < 1 || ny > m || vis[nx][ny] || !mp[nx][ny]) continue;//顺序有讲究,先看越界。如果有标记,或者是0的话无法搜索。
vis[nx][ny] = 1;
cnt += mp[nx][ny];//统计一下
dfs(nx, ny);
}
}
void solve() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> mp[i][j];
vis[i][j] = 0;
}
}
int ans = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (vis[i][j] || !mp[i][j]) continue;//如果是0或者是有标记的正数
cnt = mp[i][j];
vis[i][j] = 1;//别忘记!!!不然会寄
dfs(i, j);
ans = max(ans, cnt);
}
}
cout << ans << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
int T = 1;
cin >> T;
while (T--) {
solve();
}
return 0;
}
F. Forever Winter(简单的图)
题意:给你一个雪花图的联通关系,让你判断雪花的第一分支数和第二分支数。
思路:本题并不需要什么高深的东西,只需要统计一下每个点的度数即可。首先,如果说这里有三种度数,1 1 1 x x x x y 那么唯一的y度数必定是第一分支数,多个x必定是第二分支数(注意这里xy均大于1),1是叶子,无妨。如果说这里是两种度数的话 1 1 1 x x x那么第一分支数就是x 的数目 -1,第二分支数x - 1.
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define eps 1e-9
using namespace std;
const int N = 105;
int in[N];
void solve() {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) in[i] = 0;
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
in[u]++;
in[v]++;
}
map<int, int> mp;
for (int i = 1; i <= n; i++) {
mp[in[i]]++;
}
int x = -1, y;
for (auto i : mp) {
if (i.second == 1) x = i.first;//唯一的度数是第一分支数
if (i.first != 1 && i.second != 1) y = i.first - 1;//度数 - 1(来自中心的一度)
}
if (x == -1) x = y + 1;//恢复原来的度数
cout << x << ' ' << y << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
int T = 1;
cin >> T;
while (T--) {
solve();
}
return 0;
}
G. Hits Different(二维前缀和)
题意:求出矩阵的和。
思路:
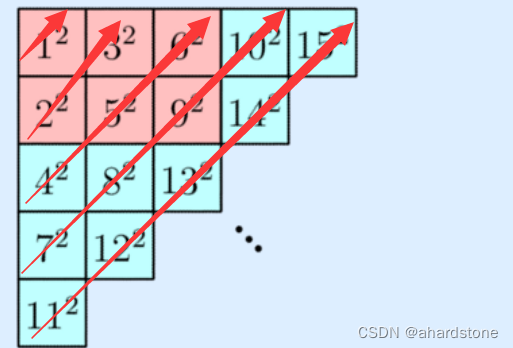
我借用了一下官方题解的图,红色的箭头是我遍历的方向。i枚举是第几斜层,j体现坐标变化。
二维前缀和比较简单。
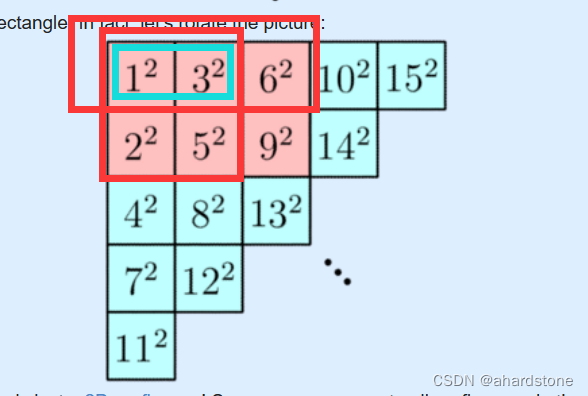
俩红减去蓝色,加上新的数。
还有一个要注意的点是,这个是1 + 2 + 3 + 4 … 1000是不够的,还有就是小心RE,ans+5是不够的。
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define eps 1e-9
using namespace std;
const int N = 2e6 + 5;
ll ans[N], sum[1455][1455];
void init() {
ll cur = 1;
for (int i = 1; i <= 1450; i++) {
for (int j = 0; j < i; j++) {
sum[i - j][j + 1] = sum[i - j - 1][j + 1] + sum[i - j][j] - sum[i - j - 1][j] + cur * cur;
ans[cur++] = sum[i - j][j + 1];
}
}
// cout << cur << '\n';
}
void solve() {
int n;
cin >> n;
cout << ans[n] << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
int T = 1;
init();
cin >> T;
while (T--) {
solve();
}
return 0;
}
H. Don’t Blame Me(状态压缩dp)
题意:给你一个数组,让你求出所有元素按位与和的值的1的数目是k的方法数
思路:定义dp状态,表示在前i个数,子序列元素按位与和的值为j的方法数。
对于i的所有j的值的方法数,来源有三种,一种是前i - 1内部的方法数的贡献,一种是第i个数单独的贡献,一种是前i-1数和第i个数相互作用的贡献。__builtin_popcount()统计二进制数中1的数目。
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define eps 1e-9
using namespace std;
const int N = 2e5 + 5, mod = 1e9 + 7;
ll f[N][70];
void solve() {
int n, k;
cin >> n >> k;
for (int i = 0; i <= n; i++) {
for (int j = 0; j < 64; j++) {
f[i][j] = 0;
}
}
for (int i = 1; i <= n; i++) {
int x;
cin >> x;
for (int j = 0; j < 64; j++) {
f[i][j] = (f[i][j] + f[i - 1][j]) % mod;
f[i][j & x] = (f[i][j & x] + f[i][j]) % mod;
}
f[i][x] = (f[i][x] + 1) % mod;
}
ll ans = 0;
for (int i = 0; i < 64; i++) {
if (__builtin_popcount(i) == k) ans = (ans + f[n][i]) % mod;
}
cout << ans << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
int T = 1;
cin >> T;
while (T--) {
solve();
}
return 0;
}