文章目录

神经网络
- 简介
- 学习路径
- 分类
多层感知器（MLP）
- 神经网络认识
- 两层神经网络
- - 输入层
  - 从输入层到隐藏层
  - 从隐藏层到输出层
  - 激活层
  - 输出的正规化
  - 如何衡量输出的好坏
  - 反向传播与参数优化
  - 过拟合
- BP算法推导
- tensorflow实战

神经网络

简介

神经网络是一种基于生物神经系统结构和功能特点而设计的人工神经网络模型，具有很强的自适应性和非线性映射能力。神经网络由多个神经元（或称节点）组成，这些神经元通过连接权重相互连接，构成多层的网络结构。每个神经元接收到来自其它神经元的信号，并将这些信号加权线性组合后通过激活函数进行非线性转换，最终输出给下一层神经元或输出层。

学习机器学习后，学习神经网络可以帮助你更深入地理解模式识别和人工智能领域的基础知识。神经网络在很多领域都有广泛的应用，例如计算机视觉、自然语言处理、语音识别等。学习神经网络可以让你掌握这些领域中最前沿的技术，并且能够应用这些技术来解决具体的问题。同时，神经网络的学习方法和算法也是机器学习的重要组成部分，学习神经网络可以帮助你更好地理解机器学习的原理和技术，从而更好地应用机器学习来解决实际问题。

学习路径

如果你已经学过机器学习，那么开始学习神经网络，可以从多层感知器（Multilayer Perceptron，简称 MLP）神经网络入手。 MLP 是最基本的神经网络模型之一，它的结构比较简单，易于理解和实现，同时又有很好的可扩展性和通用性，可以应用于分类、回归等多种任务。学习 MLP 之后，你可以进一步学习卷积神经网络（Convolutional Neural Networks，简称 CNN）和循环神经网络（Recurrent Neural Networks，简称 RNN），它们分别用于计算机视觉和自然语言处理等特定领域的问题。总之，建议先从 MLP 入手，逐渐深入学习其他类型的神经网络。

多层感知器（MLP）

MLP神经网络属于前馈神经网络（Feedforward Neural Network）的一种。在网络训练过程中，需要通过反向传播算法计算梯度，将误差从输出层反向传播回输入层，用于更新网络参数。这个过程中需要使用反向传播算法来计算梯度，并且在某些类型的神经网络中，例如循环神经网络（RNN），也存在反馈回路。除了MLP，其他常见的前馈神经网络包括卷积神经网络（CNN）和循环神经网络（RNN）等。

神经网络认识

我们以一个简单的例子来认识神经网络，只是为了理解其中的一些概念。
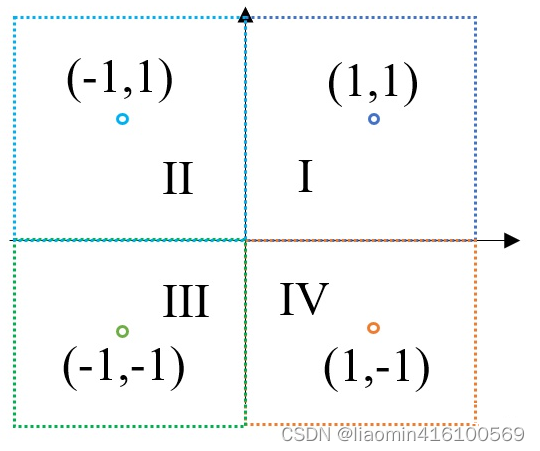
我们已知四个数据点(1,1)(-1,1)(-1,-1)(1,-1)，这四个点分别对应I~IV象限（也就是数据属于的类别），如果这时候给我们一个新的坐标点（比如(2,2)），那么它应该属于哪个象限呢？（没错，当然是第I象限，但我们的任务是要让机器知道，机器不知道有象限这个东西啊，他只能根据历史数据的经验推断）
在这里插入图片描述

两层神经网络

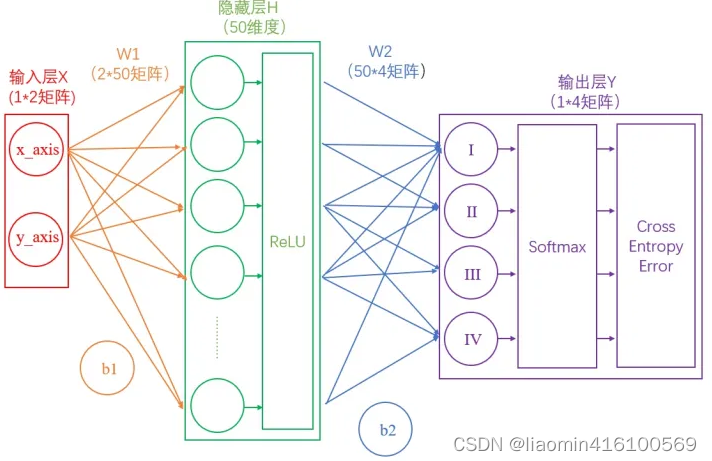
这里我们构建一个两层神经网络，理论上两层神经网络已经可以拟合任意函数。这个神经网络的结构如下图：
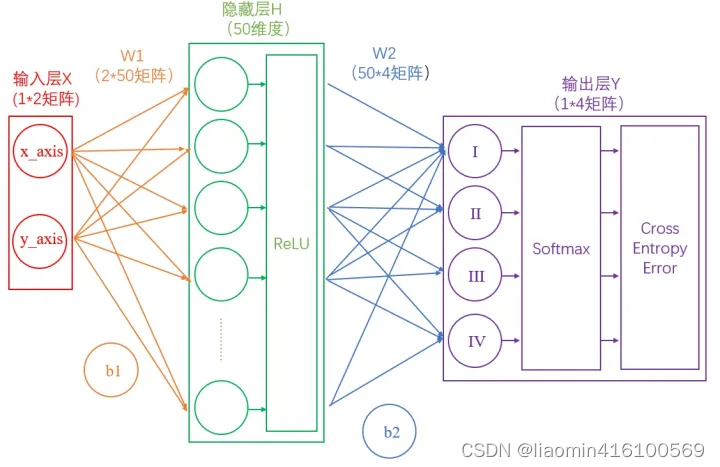
在这里插入图片描述
首先我们去掉途中难懂的东西

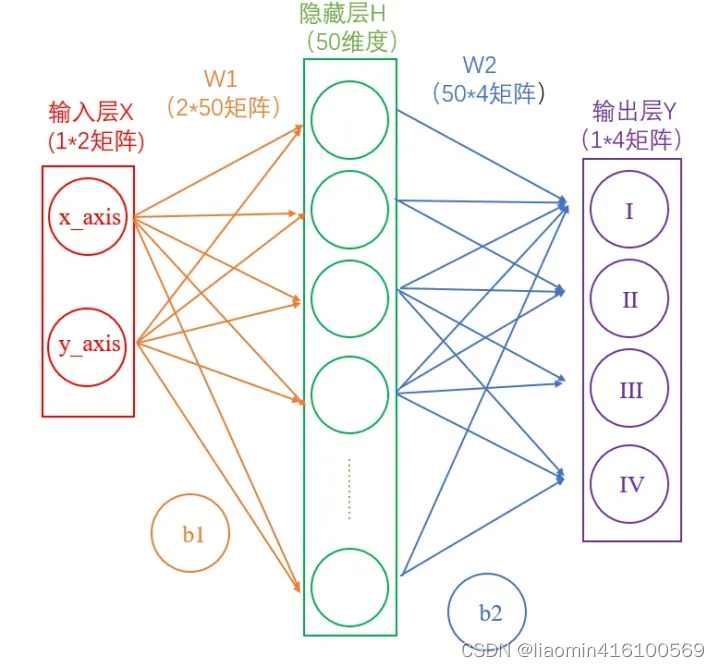
输入层

在我们的例子中，输入层是坐标值，例如（1,1），这是一个包含两个元素的数组，也可以看作是一个12的矩阵。输入层的元素维度与输入量的特征息息相关，如果输入的是一张3232像素的灰度图像，那么输入层的维度就是32*32。
因为整个神经网络的目的是为了训练出一个模型，所以输入的是历史数据，历史数据有一个确定的输出label，模型出来后，直接使用模型就可以分类出输入的数据的输出
这里输入的数据为:

[
[1,1],
[-1,1],
[-1,-1],
[1,-1]
]

从输入层到隐藏层

连接输入层和隐藏层的是W1和b1。由X计算得到H十分简单，就是矩阵运算：
$H = w * x + b$
果你学过线性代数，对这个式子一定不陌生,可以理解为w是一个权重(权重越高，这个特征也就越重要)，b是一个偏置，如果有多个特征那么就有个w，还记得 $w^T*x$ 。
在这里插入图片描述
如上图中所示，在设定隐藏层为50维（也可以理解成50个神经元）之后，矩阵H的大小为（4*50）的矩阵。

也就是说50个神经元就是一个矩阵50个特征，每一行就是他的w值，这里输入层总共两个维度，所有只有w1和w2，b值这里就不说了，假设为0
在这里插入图片描述
这里我们可以简化最终得到4*50的意义

从隐藏层到输出层

连接隐藏层和输出层的是W2和b2,输入就是隐藏层输入的H值。同样是通过矩阵运算进行的：
$Y = w 2 * H + b 2$
最终输出层，最终是4个象限
H是450的矩阵，输出层的w2矩阵就是个504,最终得到一个4*4的矩阵
这里不详细画图了，大概意义如下。

H是4*50的矩阵其实是一个列是神经元50个，行是4个数据集的经过第一轮计算的输出值H，隐藏层的目的就是计算出一个H值。
输出层的 w矩阵是50*4，目的是为了将50个神经元压缩到4个输出特征，也就是每一个数据集在4个象限的概率。所以最终输出是4*4

激活层

通过上述两个线性方程的计算，我们就能得到最终的输出Y了，但是如果你还对线性代数的计算有印象的话，应该会知道：一系列线性方程的运算最终都可以用一个线性方程表示。也就是说，上述两个式子联立后可以用一个线性方程表达。对于两次神经网络是这样，就算网络深度加到100层，也依然是这样。这样的话神经网络就失去了意义。
所以这里要对网络注入灵魂：激活层。
简而言之，激活层是为矩阵运算的结果添加非线性的

激活层是神经网络中的一种层，其作用是在输入信号和输出信号之间添加一个非线性的转换函数，使得网络可以更好地学习和表示复杂的非线性关系。激活层的意义在于增加模型的非线性表达能力，使得神经网络可以更好地处理复杂的输入数据，例如图像、文本和语音等。激活函数的选择也非常重要，不同的激活函数具有不同的特点。
激活层常用的激活函数三种，分别是阶跃函数、Sigmoid和ReLU，如下图：
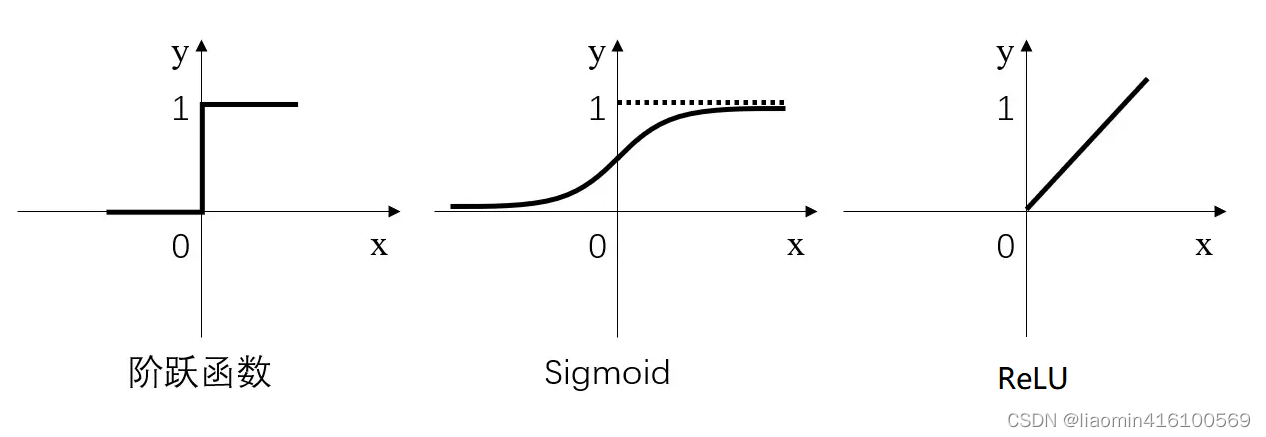
在这里插入图片描述

阶跃函数：当输入小于等于0时，输出0；当输入大于0时，输出1。
Sigmoid：当输入趋近于正无穷/负无穷时，输出无限接近于1/0。
ReLU：当输入小于0时，输出0；当输入大于0时，输出等于输入。

其中，阶跃函数输出值是跳变的，且只有二值，较少使用；Sigmoid函数在当x的绝对值较大时，曲线的斜率变化很小（梯度消失），并且计算较复杂；ReLU是当前较为常用的激活函数。

激活函数具体是怎么计算的呢？
假如经过公式H=X*W1+b1计算得到的H值为：(1,-2,3,-4,7…)，那么经过阶跃函数激活层后就会变为(1,0,1,0,1…)，经过ReLU激活层之后会变为(1,0,3,0,7…)。

需要注意的是，每个隐藏层计算（矩阵线性运算）之后，都需要加一层激活层，要不然该层线性计算是没有意义的。
此时的神经网络变成了如下图所示的形式：
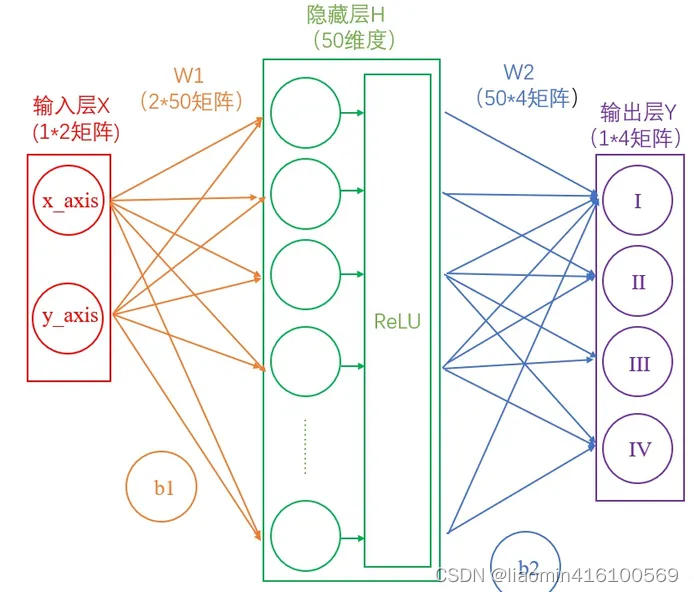
在这里插入图片描述
我们都知道（？）神经网络是分为“训练”和“使用”两个步骤的。如果是在“使用”的步骤，图4就已经完成整个过程了，在求得的Y（大小为4*4）矩阵中，当前样本数值最大的就代表着当前分类。

但是对于用于“训练”的网络，上图还远远不够。起码当前的输出Y，还不够“漂亮”。

输出的正规化

假设某个样本输出Y的值可能会是(3,1,0.1,0.5)这样的矩阵，诚然我们可以找到里边的最大值“3”，从而找到对应的分类为I，但是这并不直观。我们想让最终的输出为概率，也就是说可以生成像(90%,5%,2%,3%)这样的结果，这样做不仅可以找到最大概率的分类，而且可以知道各个分类计算的概率值。
具体是怎么计算的呢？
计算公式如下：
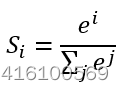
在这里插入图片描述
简单来说分三步进行：（1）以e为底对所有元素求指数幂；（2）将所有指数幂求和；（3）分别将这些指数幂与该和做商。

这样求出的结果中，所有元素的和一定为1，而每个元素可以代表概率值。

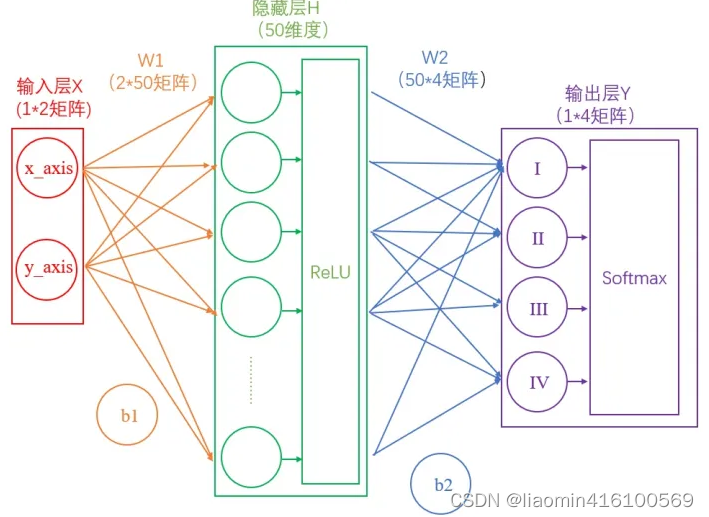
我们将使用这个计算公式做输出结果正规化处理的层叫做“Softmax”层。此时的神经网络将变成如下图所示：
在这里插入图片描述

如何衡量输出的好坏

通过Softmax层之后，我们得到了I，II，III和IV这四个类别分别对应的概率，但是要注意，这是神经网络计算得到的概率值结果，而非真实的情况。

比如，Softmax输出的结果是(90%,5%,3%,2%)，真实的结果是(100%,0,0,0)。虽然输出的结果可以正确分类，但是与真实结果之间是有差距的，一个优秀的网络对结果的预测要无限接近于100%，为此，我们需要将Softmax输出结果的好坏程度做一个“量化”。

一种直观的解决方法，是用1减去Softmax输出的概率，比如1-90%=0.1。不过更为常用且巧妙的方法是，求对数的负数。

还是用90%举例，对数的负数就是：-log0.9=0.046

可以想见，概率越接近100%，该计算结果值越接近于0，说明结果越准确，该输出叫做“交叉熵损失（Cross Entropy Error）”。

我们训练神经网络的目的，就是尽可能地减少这个“交叉熵损失”。
在这里插入图片描述

反向传播与参数优化

上面的过程其实就是神经网络的正向传播过程，一句话复习一下：神经网络的传播都是形如Y=WX+b的矩阵运算；为了给矩阵运算加入非线性，需要在隐藏层中加入激活层；输出层结果需要经过Softmax层处理为概率值，并通过交叉熵损失来量化当前网络的优劣。

算出交叉熵损失后，就要开始反向传播了。其实反向传播就是一个参数优化的过程，优化对象就是网络中的所有W和b（因为其他所有参数都是确定的）。

神经网络的神奇之处，就在于它可以自动做W和b的优化，在深度学习中，参数的数量有时会上亿，不过其优化的原理和我们这个两层神经网络是一样的。

神经网络需要反复迭代。如上述例子中，第一次计算得到的概率是90%，交叉熵损失值是0.046；将该损失值反向传播，使W1,b1,W2,b2做相应微调；再做第二次运算，此时的概率可能就会提高到92%，相应地，损失值也会下降，然后再反向传播损失值，微调参数W1,b1,W2,b2。依次类推，损失值越来越小，直到我们满意为止。

此时我们就得到了理想的W1,b1,W2,b2。

具体参考 BP算法怎推导章节

内容参考：https://zhuanlan.zhihu.com/p/65472471

过拟合

Dropout是一种在神经网络中用于防止过拟合的技术。它是通过在训练期间随机将一些节点的输出设置为0来实现的。具体来说，每个节点有一定的概率被“关闭”，即其输出被设置为0。这样，节点之间的连接就会被随机断开，从而迫使网络学习更加鲁棒的特征，而不是依赖特定的节点或连接。这种随机性可以被看作是一种正则化技术，可以有效地防止过拟合。

过拟合是指模型在训练数据上表现很好，但在测试数据上表现不佳的现象。这通常是由于模型过于复杂，而训练数据又过少或过于噪声导致的。通过使用Dropout技术，我们可以减少模型的复杂度，并使其更加适应不同的训练数据。这样，我们就可以更好地泛化模型，从而在测试数据上获得更好的表现。

假设我们有一个二分类任务，需要从图像中识别猫和狗。我们使用卷积神经网络进行训练，但由于数据集较小，容易出现过拟合的问题。

为了解决这个问题，我们可以在卷积神经网络中添加Dropout层。例如，我们可以在全连接层之前添加一个Dropout层，将其输出概率设置为0.5。这意味着在每个训练批次中，该层中的一半节点的输出将被随机设置为0。这样，网络就不会过于依赖特定节点或连接，并且可以更好地适应不同的训练数据。

BP算法推导

定义

首先来一个反向传播算法的定义（转自维基百科）：反向传播（英语：Backpropagation，缩写为BP）是“误差反向传播”的简称，是一种与最优化方法（如梯度下降法）结合使用的，用来训练人工神经网络的常见方法。该方法对网络中所有权重计算损失函数的梯度。这个梯度会反馈给最优化方法，用来更新权值以最小化损失函数。（误差的反向传播）

算法讲解

如果去问一下了解BP算法的人“BP算法怎推导？”，大概率得到的回答是“不就是链式求导法则嘛”，我觉得这种答案对于提问题的人来说没有任何帮助。BP的推导需要链式求导不错，但提问者往往想得到的是直观的回答，毕竟理解才是王道。直观的答案，非图解莫属了。
注：下图的确是反向传播算法，但不是深度学习中的backprop，不过backward的大体思想是一样的，毕竟误差没法从前往后计算啊。（在深度学习中操作的是计算图—Computational graph），如果暂时不理解上面那句话，你可以当我没说过，不要紧~（手动?）

下面通过两组图来进行神经网络前向传播和反向传播算法的讲解，第一组图来自国外某网站，配图生动形象。如果对你来说，单纯的讲解理解起来比较费劲，那么可以参考第二组图——一个具体的前向传播和反向传播算法的例子。相信就算是刚刚入门的小白（只要有一点点高等数学基础知识），也一定可以理解反向传播算法！

首先拿一个简单的三层神经网络来举例，如下：
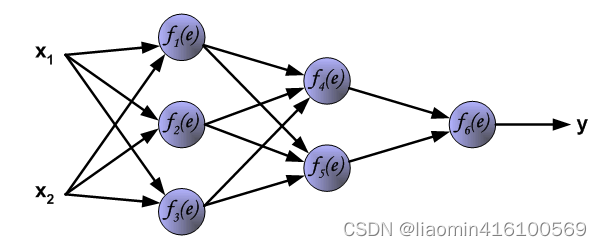
在这里插入图片描述
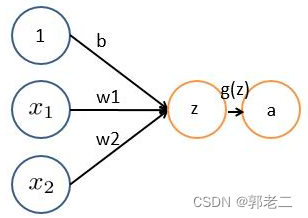
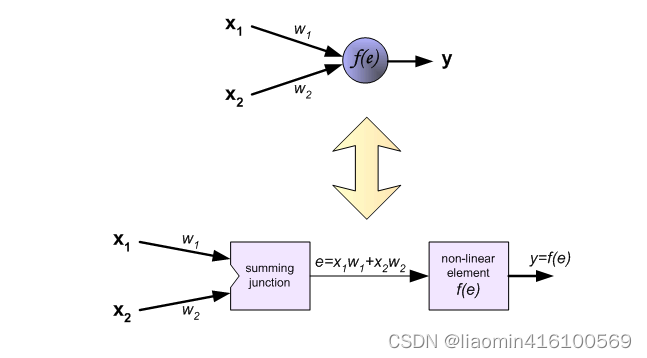
每个神经元由两部分组成，第一部分（e）是输入值和权重系数乘积的和，第二部分（f(e)）是一个激活函数（非线性函数）的输出， y=f(e)即为某个神经元的输出，如下：

前向传播

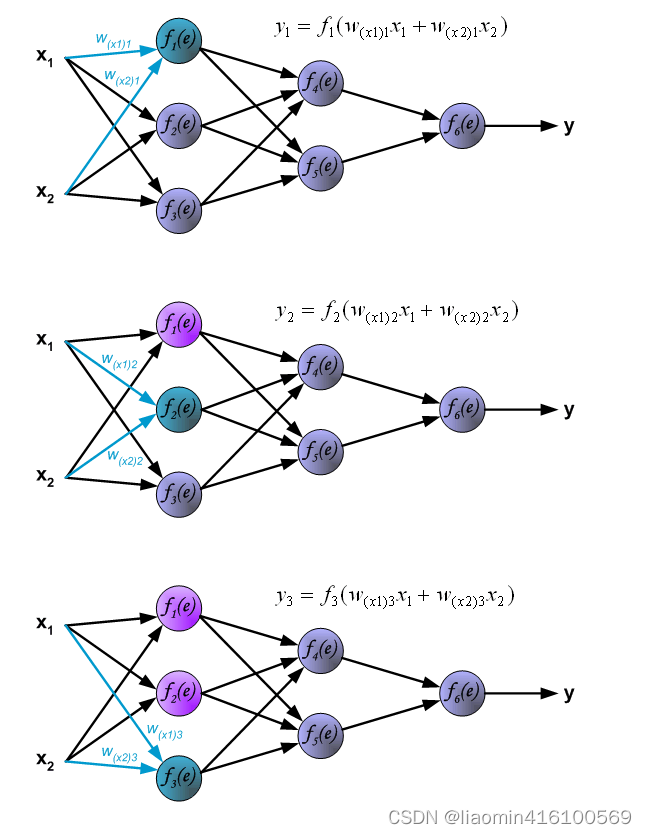
第一层神经网络传播

其中 $w_{x1}1$ 表示x1对应第一个神经元的w值， $w_{x2}1$ ，表示x2对应对一个神经元的w值。

在这里插入图片描述
第二层神经网络传播

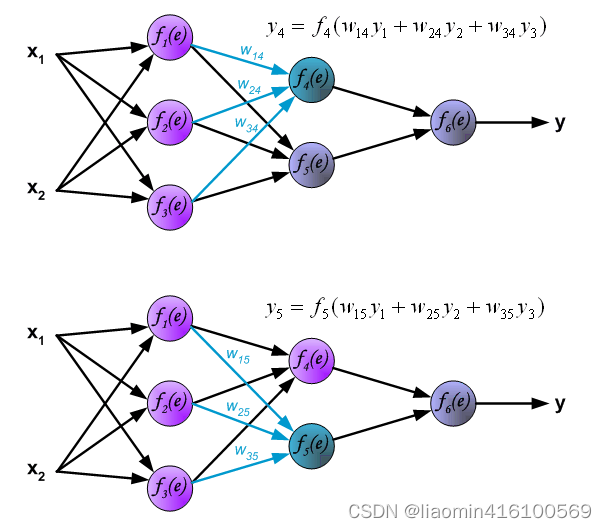
第三层神经网络传播

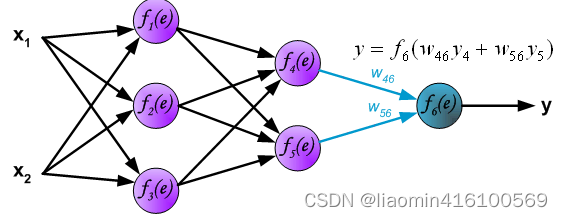
反向传播

到这里为止，神经网络的前向传播已经完成，最后输出的y就是本次前向传播神经网络计算出来的结果（预测结果），但这个预测结果不一定是正确的，要和真实的标签（z）相比较，计算预测结果和真实标签的误差（ $\delta$ ），如下：
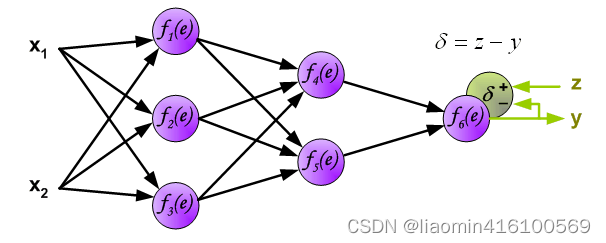
在这里插入图片描述
下面开始计算每个神经元的误差（ $\delta$ ）

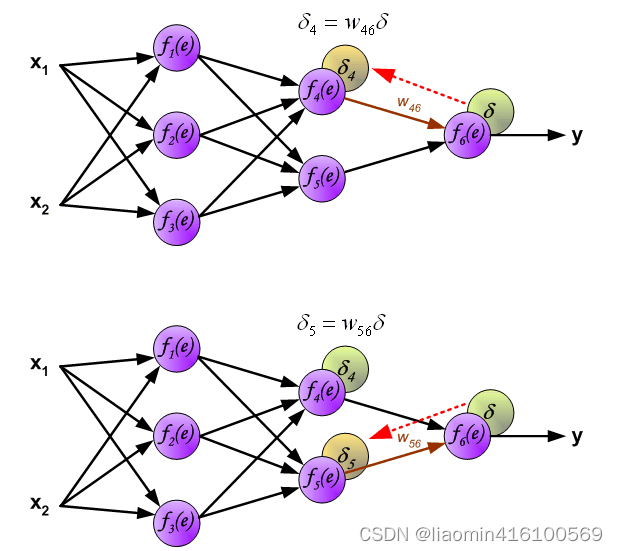
计算第一层误差

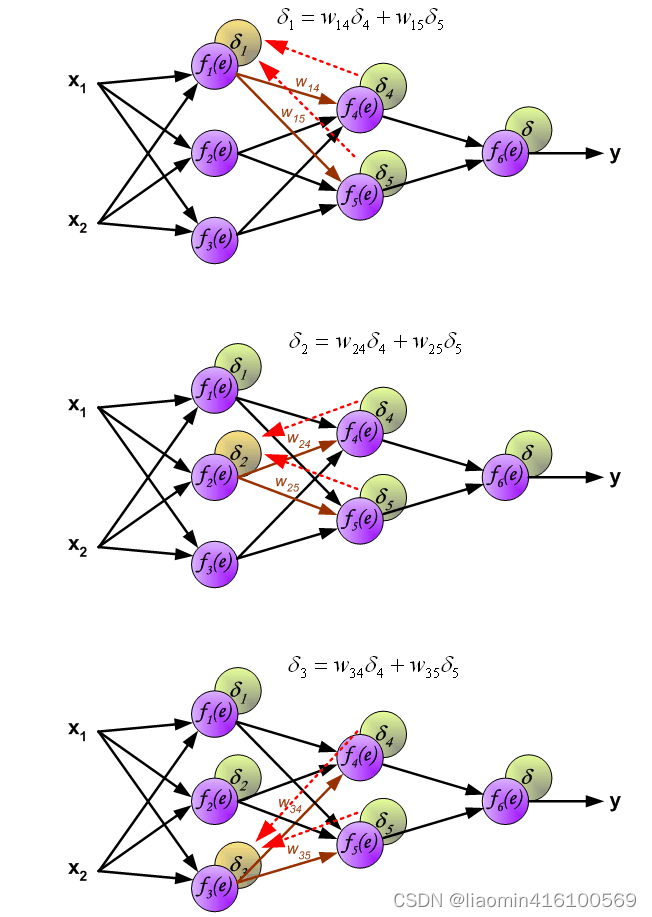
下面开始利用反向传播的误差，计算各个神经元（权重）的导数，开始反向传播修改权重

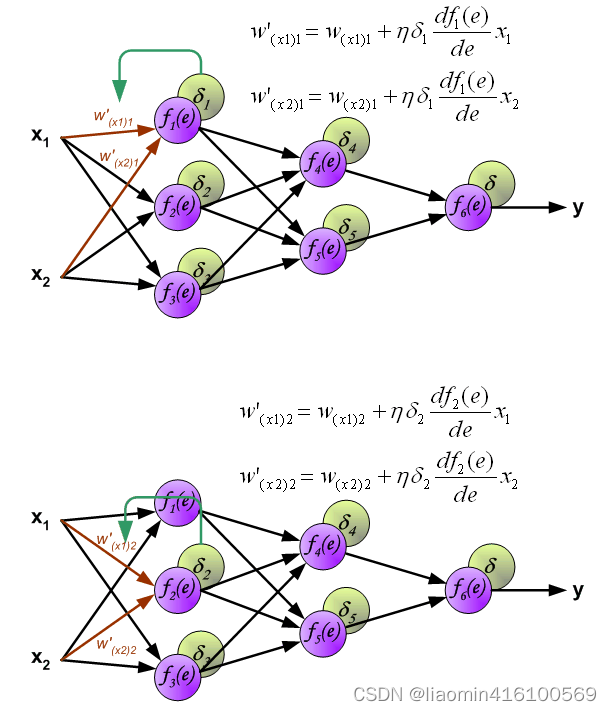
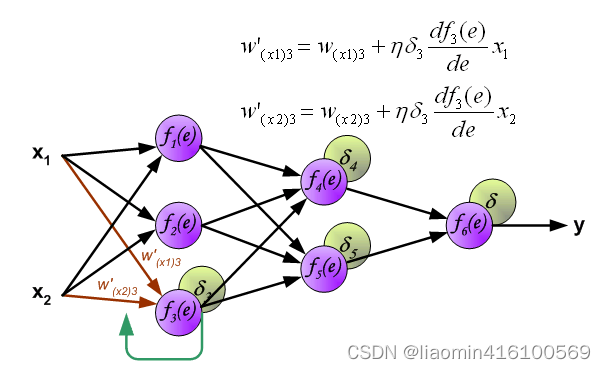
计算第二次的w

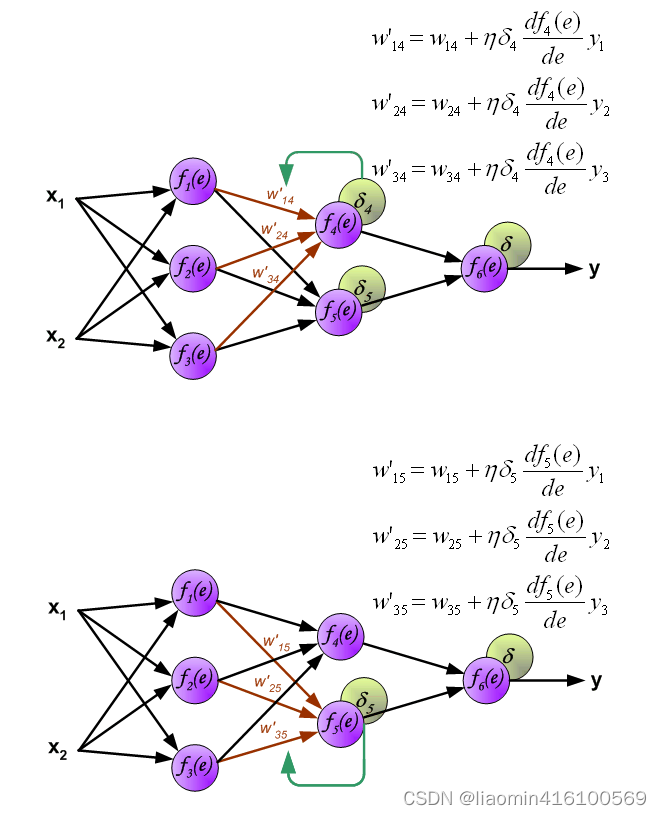
计算第三层

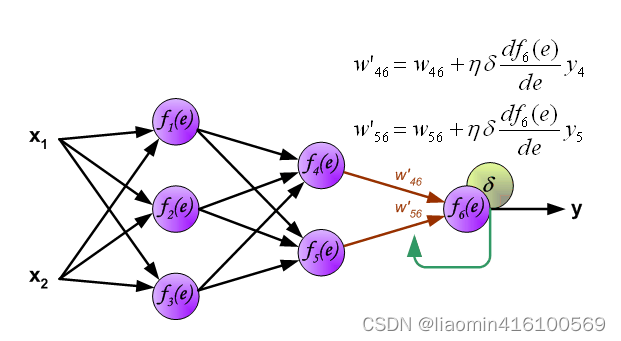
到此为止，整个网络的前向，反向传播和权重更新已经完成

具体实例

就算上面的所有东西你都看的迷迷糊糊，通过下面的例子，相信绝大多数人也能很轻松的理解BP算法。如图是一个简单的神经网络用来举例：
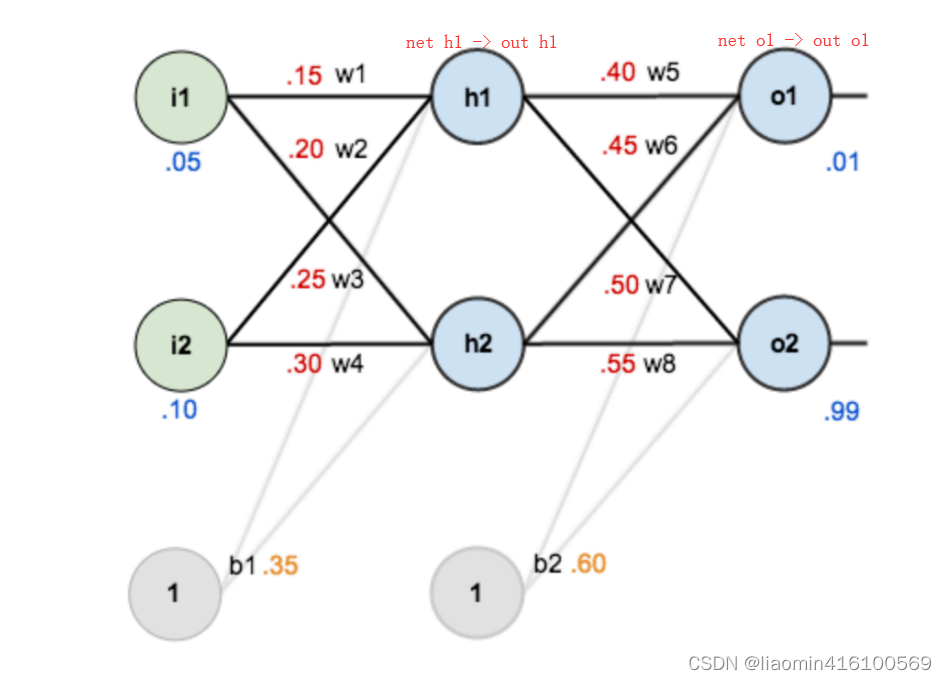
在这里插入图片描述
下面是前向（前馈）运算（激活函数为sigmoid）：

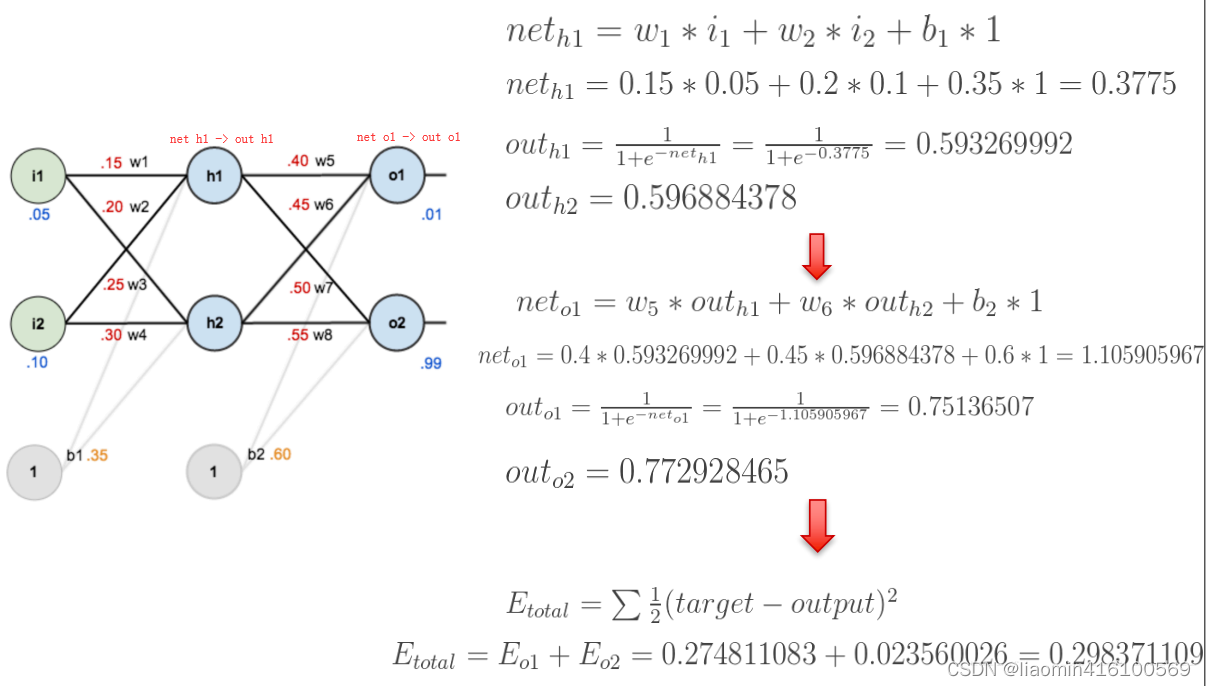
下面是反向传播（求网络误差对各个权重参数的梯度）：

我们先来求最简单的，求误差E对w5的导数。首先明确这是一个“链式求导”过程，要求误差E对w5的导数，需要先求误差E对out o1的导数，再求out o1对net o1的导数，最后再求net o1对w5的导数，经过这个链式法则，我们就可以求出误差E对w5的导数（偏导），如下图所示：
在这里插入图片描述
导数（梯度）已经计算出来了，下面就是反向传播与参数更新过程：

上面的图已经很显然了，如果还看不懂真的得去闭门思过了（开玩笑~），耐心看一下上面的几张图，一定能看懂的。

如果要想求误差E对w1的导数，误差E对w1的求导路径不止一条，这会稍微复杂一点，但换汤不换药，计算过程如下所示：
在这里插入图片描述

bp推导参考：https://blog.csdn.net/ft_sunshine/article/details/90221691

tensorflow实战

加载数据集

keras.datasets.mnist 是 Keras 框架内置的一个手写数字数据集，包含了 60,000 张训练图片和 10,000 张测试图片。每张图片都是 28x28 像素的灰度图像，每个像素的取值范围为 0 到 255。该数据集常用于机器学习领域中的图像分类和数字识别任务。

keras.datasets.mnist 的返回值是一个元组 (x_train, y_train), (x_test, y_test)，分别表示训练集和测试集。其中 x_train 和 x_test 分别是形状为 (60000, 28, 28) 和 (10000, 28, 28) 的 numpy 数组，表示图像数据。y_train 和 y_test 则是形状为 (60000,) 和 (10000,) 的 numpy 数组，表示对应的图像标签，即每张图片所代表的数字。
记载数据集，并绘制前20张图片

#%%

from tensorflow.keras.datasets import mnist
import matplotlib.pyplot as plt

# 加载数据集
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_test_ori=x_test 
# 打印数据集信息
print('训练集图像数据形状：', x_train.shape)
print('训练集标签数据形状：', y_train.shape)
print('测试集图像数据形状：', x_test.shape)
print('测试集标签数据形状：', y_test.shape)

# 绘制前20张训练集图像
plt.figure(figsize=(10, 10))
for i in range(20):
    plt.subplot(5, 5, i+1)
    plt.xticks([])
    plt.yticks([])
    plt.grid(False)
    plt.imshow(x_train[i], cmap=plt.cm.binary)
    plt.xlabel(y_train[i])
plt.show()

输出

训练集图像数据形状： (60000, 28, 28)
训练集标签数据形状： (60000,)
测试集图像数据形状： (10000, 28, 28)
测试集标签数据形状： (10000,)

在这里插入图片描述

默认图片下载路径在 ~/.keras/datasets ，window下：C:\Users\当前用户名.keras\datasets,大小估计10MB左右。

数据预处理

x_train = x_train.reshape(x_train.shape[0], 784).astype('float32') / 255
x_test = x_test.reshape(x_test.shape[0], 784).astype('float32') / 255
y_train = keras.utils.to_categorical(y_train, 10)
y_test = keras.utils.to_categorical(y_test, 10)

在上面的代码中，我们将输入数据的维度从 28x28 转换为 784，因为我们处理的数据一般都是一个矩阵，一行代表一个数据样本，需要转换成784*1的数据，并将像素值的范围从 0-255 缩放到 0-1 之间。同时，我们将标签数据进行 one-hot 编码，将其转换为一个 10 维的向量，每个维度代表一个数字。

one-host编码

One-hot编码是一种将离散型变量转换为连续型变量的技术，在机器学习和深度学习中广泛应用。它将每个离散型变量的取值都编码为一个二进制位，其中只有一个二进制位为1，其余二进制位为0。举例说明如下：

假设有一个离散型变量“颜色”，它的可能取值为“红色”、“黄色”和“蓝色”。我们可以将这三个取值编码为长度为3的二进制向量，如下所示：

红色：[1, 0, 0]

黄色：[0, 1, 0]

蓝色：[0, 0, 1]

这个编码方式就是one-hot编码。在机器学习中，我们可以使用这个编码方式来处理离散型变量，使其成为连续型变量，方便模型的学习和使用。

keras.utils.to_categorical()

keras.utils.to_categorical()函数将整数型的类别标签转换成了独热编码（one-hot encoding）的形式。在独热编码中，每个类别标签被表示为一个长度等于类别总数的向量，其中该类别标签所对应的位置值为1，其余位置为0。

对于手写数字识别任务，共有10个类别，即数字0到9，因此需要将标签向量转换为10维的独热编码。

例如，如果原始标签为5，则转换后的独热编码为[0, 0, 0, 0, 0, 1, 0, 0, 0, 0]，其中第6个位置（从0开始）的值为1，表示原始标签为5。

这样做的目的是为了让神经网络更好地理解类别之间的差异和相似性，以便更准确地进行分类预测。

构造多层感知器模型

我们使用 keras.Sequential 构建模型，该模型包含一个输入层、一个隐藏层和一个输出层。输入层的维度为 784（即每个图片的像素数），隐藏层包含 512 个神经元，激活函数为 ReLU，输出层包含 10 个神经元，激活函数为 softmax。同时，我们使用 Dropout 防止过拟合。

# 构建模型
model = tf.keras.Sequential([
    tf.keras.layers.Dense(512, activation='relu', input_shape=(784,)),
    tf.keras.layers.Dropout(0.2),
    tf.keras.layers.Dense(10, activation='softmax')
])

tf.keras.Sequential

keras.Sequential是Keras中的一个类，用于快速搭建神经网络模型。它提供了一个简单的方法来创建顺序模型，即一系列层按照顺序堆叠在一起的模型。在keras.Sequential中，可以通过添加层的方式来搭建神经网络。

keras.Sequential的定义如下：

keras.Sequential(
    layers=None, 
    name=None
)

其中，layers是一个列表，包含了按照顺序堆叠在一起的层；name是模型的名称。
上面使用keras.Sequential创建简单神经网络的例子：

model = tf.keras.Sequential([
    tf.keras.layers.Dense(512, activation='relu', input_shape=(784,)),
    tf.keras.layers.Dropout(0.2),
    tf.keras.layers.Dense(10, activation='softmax')
])

我们创建了一个包含三层的神经网络模型。第一层是一个全连接层，包含512个神经元，使用ReLU激活函数，输入形状为(784,)。第二层是一个Dropout层，第三层是一个全连接层包含10个神经元，使用Softmax激活函数。

keras.layers.Dense

keras.layers.Dense是Keras中的一个类，用于创建全连接层。全连接层是神经网络中最基本的一种层，它的每一个神经元都与上一层的每一个神经元相连。keras.layers.Dense可以用于创建输入层、输出层和隐藏层。

keras.layers.Dense的定义如下：

keras.layers.Dense(
    units, 
    activation=None, 
    use_bias=True, 
    kernel_initializer='glorot_uniform', 
    bias_initializer='zeros', 
    kernel_regularizer=None, 
    bias_regularizer=None, 
    activity_regularizer=None, 
    kernel_constraint=None, 
    bias_constraint=None, 
    **kwargs
)

其中，units表示该层的神经元数量；activation表示该层的激活函数；use_bias表示是否使用偏置；kernel_initializer表示权重矩阵的初始化方法；bias_initializer表示偏置向量的初始化方法；kernel_regularizer、bias_regularizer、activity_regularizer表示正则化项；kernel_constraint、bias_constraint表示约束项。

下面是一个使用keras.layers.Dense创建全连接层的例子：

import tensorflow.keras as keras
layer =  tf.keras.layers.Dense(512, activation='relu', input_shape=(784,)),

在这个例子中，我们创建了一个包含512个神经元的全连接层。激活函数为ReLU，输入形状为(784,)，表示该层的输入数据是一个长度为784的向量。

keras.layers.Dense的一些常用参数和方法：

units：该层的神经元数量；
activation：该层的激活函数；
use_bias：是否使用偏置；
kernel_initializer：权重矩阵的初始化方法；
bias_initializer：偏置向量的初始化方法；
kernel_regularizer、bias_regularizer、activity_regularizer：正则化项；
kernel_constraint、bias_constraint：约束项；
layer.get_weights()：获取该层的权重矩阵和偏置向量；
layer.set_weights(weights)：设置该层的权重矩阵和偏置向量。
以上就是keras.layers.Dense的一些基本信息和使用方法。

keras.layers.Dropout

tf.keras.layers.Dropout是一种在神经网络中应用的正则化方法，用于减少过拟合的影响。在训练期间，Dropout层会随机地将输入张量的一部分元素设置为0，从而强制网络学习更健壮的特征表示，防止过拟合。具体来说，Dropout层以一定的概率（通常为0.5）随机地将输入张量的一部分神经元输出设为0，这些被屏蔽的神经元将不会参与前向传播和反向传播。这样做可以强制网络在训练过程中学习到更多的特征，并且使得网络对于输入的微小变化更加稳健。

在tf.keras.layers.Dropout中，可以设置一个rate参数，来控制屏蔽神经元的比例，即随机将输入张量的多少个元素置为0。具体来说，如果rate=0.5，则代表在训练过程中随机选取50%的神经元输出为0，而在测试过程中不会进行任何操作。同时，可以将tf.keras.layers.Dropout层放在神经网络的任何位置，通常放在全连接层之后，以减少过拟合的影响。

Dropout层的主要作用是减少过拟合的影响，从而提高模型的泛化能力。通过随机屏蔽部分神经元，Dropout层可以强制网络学习到更健壮的特征表示，并且使得网络对于输入的微小变化更加稳健。这样可以增加模型的鲁棒性，提高模型的泛化能力，从而使得模型在测试集上表现更好。

需要注意的是，在测试过程中不应该使用Dropout层，因为测试过程需要对整个模型进行前向传播，而不是将部分神经元置为0。因此，在测试过程中，需要将所有的神经元都参与前向传播，以获得更准确的预测结果。为了解决这个问题，可以在训练过程中使用Dropout层，并在测试过程中关闭Dropout层，或者根据Dropout的特性对输出进行调整。

keras.layers.其他

keras.layers 模块提供了许多常见的神经网络层类，其中一些常用的层包括：

Dense：全连接层，每个输入节点都连接到输出节点
Conv2D：二维卷积层，对图像或其他二维输入进行卷积运算
MaxPooling2D：二维最大池化层，对输入进行下采样
Dropout：随机丢弃一部分输入节点，以减少过拟合
Flatten：将输入展平为一维张量
Activation：激活函数层，如ReLU、Sigmoid、Softmax等
BatchNormalization：批量归一化层，用于加速收敛和减少过拟合
Embedding：词嵌入层，将离散的词转换为连续的向量表示
LSTM：长短时记忆循环层，用于处理时间序列数据
GRU：门控循环单元层，用于处理时间序列数据

这些层可以通过组合或堆叠来构建复杂的神经网络模型。除了这些常用的层外，keras.layers 还提供了许多其他层，如 Conv1D、Conv3D、UpSampling2D、SeparableConv2D、GlobalMaxPooling2D、GlobalAveragePooling2D等等。可以根据具体的任务需求选择合适的层。

模型训练

history = model.fit(x_train, y_train, 
                    epochs=10, 
                    batch_size=128, 
                    validation_data=(x_test, y_test))

在上面的代码中，我们使用 model.fit 进行模型训练，设置了 10 个 epochs 和 128 个批次大小。同时，我们使用测试集进行模型验证。

在每个epoch中，模型需要对整个训练数据集进行训练，而不是仅仅针对一个样本或一个batch进行训练。因此，在每个epoch中，模型需要对所有训练样本进行前向传播和反向传播，以计算出每个样本对应的误差和梯度，并使用这些梯度更新模型的权重参数。

为了加快模型训练的速度，通常会将训练数据集分成多个batch，每个batch包含若干个样本。在每个epoch中，模型会将整个训练数据集分成多个batch，然后对每个batch进行前向传播和反向传播，以更新权重参数。因此，在每个epoch中，模型需要进行多次前向传播和反向传播，才能完成对整个训练数据集的训练。

如果batch_size=128，在一次epochs中数据被拆成了128份，每一份都和512个神经元进行正向和反向传播进行梯度下降修正w和b，所以一次epochs，实际上进行了128次的梯度下降算法
如果设置成10个epoch，可以理解为128*10次梯度下降算法。
像手写数字识别的，数据进行两次epoch,进行256次梯度下降，准确率就达到97%了

注意别6w个样本一批次处理，内存罩不住啊，可能执行1个epochs都要几个小时。

模型评估

# 评估模型
test_loss, test_acc = model.evaluate(x_test, y_test)
print('Test accuracy:', test_acc)

# 预测结果
predictions = model.predict(x_test)

在上面的代码中，我们使用 model.evaluate 对模型进行评估，并使用 model.predict 进行预测。

如果运行过程中报错

InternalError: Attempting to perform BLAS operation using StreamExecutor without BLAS support
[[node sequential/dense/MatMul (defined at C:\Users\liaomin\AppData\Local\Temp\ipykernel_28392\2909523142.py:25) ]] [Op:__inference_test_function_361]

直接安装即可,gpu版本tensorflow需要blas库，cpu版本不需要

conda install blas

模型预测

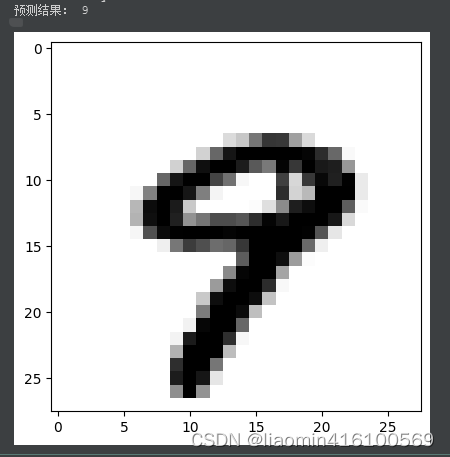
选择某个测试元素然后将图片显示出来，并使用模型预测

# 预测第10个测试数据的结果
predictions = model.predict(np.array([x_test[9]]))
print("预测结果：", np.argmax(predictions))

# 绘制第10个测试数据的图形
plt.imshow(x_test_ori[9], cmap=plt.cm.binary)
plt.show()

在这里插入图片描述

完整运行

#%%

#%%

import tensorflow as tf
from tensorflow.keras.datasets import mnist
import numpy as np
import matplotlib.pyplot as plt
# 加载数据集
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_test_ori=x_test
# 数据预处理
x_train = x_train.reshape(x_train.shape[0], 784).astype('float32') / 255
x_test = x_test.reshape(x_test.shape[0], 784).astype('float32') / 255
y_train = tf.keras.utils.to_categorical(y_train, 10)
y_test = tf.keras.utils.to_categorical(y_test, 10)

# 构建模型
model = tf.keras.Sequential([
    tf.keras.layers.Dense(512, activation='relu', input_shape=(784,)),
    tf.keras.layers.Dropout(0.2),
    tf.keras.layers.Dense(10, activation='softmax')
])

# 编译模型
model.compile(optimizer='adam',
              loss='categorical_crossentropy',
              metrics=['accuracy'])
# 训练模型
history = model.fit(x_train, y_train, 
                    epochs=2,   #这里为了节约时间，就两轮就差不多了97%正确率了，训练十次差不多0.98左右
                    batch_size=128, 
                    validation_data=(x_test, y_test))
# 评估模型
test_loss, test_acc = model.evaluate(x_test, y_test)
print('Test accuracy:', test_acc)

# 预测第10个测试数据的结果
predictions = model.predict(np.array([x_test[9]]))
print("预测结果：", np.argmax(predictions))

# 绘制第10个测试数据的图形
plt.imshow(x_test_ori[9], cmap=plt.cm.binary)
plt.show()

输出结果

Epoch 1/2

  1/469 [..............................] - ETA: 2:17 - loss: 2.2535 - accuracy: 0.1562
 13/469 [..............................] - ETA: 1s - loss: 1.3687 - accuracy: 0.6358  
 25/469 [>.............................] - ETA: 1s - loss: 0.9935 - accuracy: 0.7331
 38/469 [=>............................] - ETA: 1s - loss: 0.8118 - accuracy: 0.7775
 52/469 [==>...........................] - ETA: 1s - loss: 0.7005 - accuracy: 0.8057
 59/469 [==>...........................] - ETA: 1s - loss: 0.6644 - accuracy: 0.8137
 70/469 [===>..........................] - ETA: 1s - loss: 0.6148 - accuracy: 0.8256
 83/469 [====>.........................] - ETA: 1s - loss: 0.5690 - accuracy: 0.8376
 97/469 [=====>........................] - ETA: 1s - loss: 0.5308 - accuracy: 0.8479
111/469 [======>.......................] - ETA: 1s - loss: 0.5008 - accuracy: 0.8562
124/469 [======>.......................] - ETA: 1s - loss: 0.4797 - accuracy: 0.8621
136/469 [=======>......................] - ETA: 1s - loss: 0.4648 - accuracy: 0.8659
145/469 [========>.....................] - ETA: 1s - loss: 0.4548 - accuracy: 0.8683
158/469 [=========>....................] - ETA: 1s - loss: 0.4398 - accuracy: 0.8727
172/469 [==========>...................] - ETA: 1s - loss: 0.4253 - accuracy: 0.8765
185/469 [==========>...................] - ETA: 1s - loss: 0.4145 - accuracy: 0.8802
199/469 [===========>..................] - ETA: 1s - loss: 0.3999 - accuracy: 0.8843
212/469 [============>.................] - ETA: 1s - loss: 0.3899 - accuracy: 0.8872
225/469 [=============>................] - ETA: 1s - loss: 0.3804 - accuracy: 0.8902
238/469 [==============>...............] - ETA: 0s - loss: 0.3700 - accuracy: 0.8933
252/469 [===============>..............] - ETA: 0s - loss: 0.3619 - accuracy: 0.8951
266/469 [================>.............] - ETA: 0s - loss: 0.3537 - accuracy: 0.8979
280/469 [================>.............] - ETA: 0s - loss: 0.3460 - accuracy: 0.9001
291/469 [=================>............] - ETA: 0s - loss: 0.3401 - accuracy: 0.9018
303/469 [==================>...........] - ETA: 0s - loss: 0.3350 - accuracy: 0.9032
316/469 [===================>..........] - ETA: 0s - loss: 0.3298 - accuracy: 0.9046
330/469 [====================>.........] - ETA: 0s - loss: 0.3250 - accuracy: 0.9061
343/469 [====================>.........] - ETA: 0s - loss: 0.3198 - accuracy: 0.9073
357/469 [=====================>........] - ETA: 0s - loss: 0.3132 - accuracy: 0.9090
368/469 [======================>.......] - ETA: 0s - loss: 0.3088 - accuracy: 0.9103
381/469 [=======================>......] - ETA: 0s - loss: 0.3051 - accuracy: 0.9115
395/469 [========================>.....] - ETA: 0s - loss: 0.3017 - accuracy: 0.9125
409/469 [=========================>....] - ETA: 0s - loss: 0.2970 - accuracy: 0.9139
423/469 [==========================>...] - ETA: 0s - loss: 0.2927 - accuracy: 0.9152
437/469 [==========================>...] - ETA: 0s - loss: 0.2889 - accuracy: 0.9163
448/469 [===========================>..] - ETA: 0s - loss: 0.2855 - accuracy: 0.9173
458/469 [============================>.] - ETA: 0s - loss: 0.2827 - accuracy: 0.9181
469/469 [==============================] - 3s 5ms/step - loss: 0.2800 - accuracy: 0.9189 - val_loss: 0.1337 - val_accuracy: 0.9610
Epoch 2/2

  1/469 [..............................] - ETA: 1s - loss: 0.1849 - accuracy: 0.9375
 13/469 [..............................] - ETA: 1s - loss: 0.1216 - accuracy: 0.9597
 25/469 [>.............................] - ETA: 1s - loss: 0.1333 - accuracy: 0.9584
 37/469 [=>............................] - ETA: 1s - loss: 0.1389 - accuracy: 0.9573
 49/469 [==>...........................] - ETA: 1s - loss: 0.1370 - accuracy: 0.9597
 63/469 [===>..........................] - ETA: 1s - loss: 0.1326 - accuracy: 0.9606
 75/469 [===>..........................] - ETA: 1s - loss: 0.1349 - accuracy: 0.9596
 86/469 [====>.........................] - ETA: 1s - loss: 0.1339 - accuracy: 0.9597
 98/469 [=====>........................] - ETA: 1s - loss: 0.1360 - accuracy: 0.9594
110/469 [======>.......................] - ETA: 1s - loss: 0.1385 - accuracy: 0.9587
123/469 [======>.......................] - ETA: 1s - loss: 0.1385 - accuracy: 0.9582
136/469 [=======>......................] - ETA: 1s - loss: 0.1371 - accuracy: 0.9591
147/469 [========>.....................] - ETA: 1s - loss: 0.1369 - accuracy: 0.9593
158/469 [=========>....................] - ETA: 1s - loss: 0.1361 - accuracy: 0.9595
170/469 [=========>....................] - ETA: 1s - loss: 0.1355 - accuracy: 0.9600
182/469 [==========>...................] - ETA: 1s - loss: 0.1360 - accuracy: 0.9601
194/469 [===========>..................] - ETA: 1s - loss: 0.1348 - accuracy: 0.9603
206/469 [============>.................] - ETA: 1s - loss: 0.1330 - accuracy: 0.9610
217/469 [============>.................] - ETA: 1s - loss: 0.1322 - accuracy: 0.9610
228/469 [=============>................] - ETA: 1s - loss: 0.1304 - accuracy: 0.9617
240/469 [==============>...............] - ETA: 1s - loss: 0.1301 - accuracy: 0.9616
252/469 [===============>..............] - ETA: 0s - loss: 0.1290 - accuracy: 0.9618
265/469 [===============>..............] - ETA: 0s - loss: 0.1276 - accuracy: 0.9623
278/469 [================>.............] - ETA: 0s - loss: 0.1264 - accuracy: 0.9625
291/469 [=================>............] - ETA: 0s - loss: 0.1253 - accuracy: 0.9629
304/469 [==================>...........] - ETA: 0s - loss: 0.1246 - accuracy: 0.9632
318/469 [===================>..........] - ETA: 0s - loss: 0.1235 - accuracy: 0.9635
332/469 [====================>.........] - ETA: 0s - loss: 0.1230 - accuracy: 0.9636
345/469 [=====================>........] - ETA: 0s - loss: 0.1220 - accuracy: 0.9641
358/469 [=====================>........] - ETA: 0s - loss: 0.1214 - accuracy: 0.9643
368/469 [======================>.......] - ETA: 0s - loss: 0.1210 - accuracy: 0.9644
380/469 [=======================>......] - ETA: 0s - loss: 0.1209 - accuracy: 0.9643
392/469 [========================>.....] - ETA: 0s - loss: 0.1206 - accuracy: 0.9645
404/469 [========================>.....] - ETA: 0s - loss: 0.1205 - accuracy: 0.9644
415/469 [=========================>....] - ETA: 0s - loss: 0.1206 - accuracy: 0.9643
427/469 [==========================>...] - ETA: 0s - loss: 0.1205 - accuracy: 0.9642
440/469 [===========================>..] - ETA: 0s - loss: 0.1201 - accuracy: 0.9644
452/469 [===========================>..] - ETA: 0s - loss: 0.1201 - accuracy: 0.9643
464/469 [============================>.] - ETA: 0s - loss: 0.1198 - accuracy: 0.9644
469/469 [==============================] - 2s 5ms/step - loss: 0.1198 - accuracy: 0.9644 - val_loss: 0.0944 - val_accuracy: 0.9716

  1/313 [..............................] - ETA: 8s - loss: 0.0785 - accuracy: 0.9688
 19/313 [>.............................] - ETA: 0s - loss: 0.0754 - accuracy: 0.9852
 36/313 [==>...........................] - ETA: 0s - loss: 0.0956 - accuracy: 0.9705
 54/313 [====>.........................] - ETA: 0s - loss: 0.1193 - accuracy: 0.9641
 73/313 [=====>........................] - ETA: 0s - loss: 0.1268 - accuracy: 0.9606
 93/313 [=======>......................] - ETA: 0s - loss: 0.1233 - accuracy: 0.9610
112/313 [=========>....................] - ETA: 0s - loss: 0.1196 - accuracy: 0.9637
130/313 [===========>..................] - ETA: 0s - loss: 0.1234 - accuracy: 0.9618
151/313 [=============>................] - ETA: 0s - loss: 0.1204 - accuracy: 0.9617
171/313 [===============>..............] - ETA: 0s - loss: 0.1137 - accuracy: 0.9642
191/313 [=================>............] - ETA: 0s - loss: 0.1163 - accuracy: 0.9638
210/313 [===================>..........] - ETA: 0s - loss: 0.1119 - accuracy: 0.9658
230/313 [=====================>........] - ETA: 0s - loss: 0.1048 - accuracy: 0.9681
245/313 [======================>.......] - ETA: 0s - loss: 0.1003 - accuracy: 0.9695
263/313 [========================>.....] - ETA: 0s - loss: 0.0979 - accuracy: 0.9699
282/313 [==========================>...] - ETA: 0s - loss: 0.0943 - accuracy: 0.9712
303/313 [============================>.] - ETA: 0s - loss: 0.0911 - accuracy: 0.9723
313/313 [==============================] - 1s 3ms/step - loss: 0.0944 - accuracy: 0.9716
Test accuracy: 0.9715999960899353