题目:
有 n 个盒子。给你一个长度为 n 的二进制字符串 boxes ,其中 boxes[i] 的值为 ‘0’ 表示第 i 个盒子是 空 的,而 boxes[i] 的值为 ‘1’ 表示盒子里有 一个 小球。
在一步操作中,你可以将 一个 小球从某个盒子移动到一个与之相邻的盒子中。第 i 个盒子和第 j 个盒子相邻需满足 abs(i - j) == 1 。注意,操作执行后,某些盒子中可能会存在不止一个小球。
返回一个长度为 n 的数组 answer ,其中 answer[i] 是将所有小球移动到第 i 个盒子所需的 最小 操作数。
每个 answer[i] 都需要根据盒子的 初始状态 进行计算。
示例 1:
输入:boxes = “110”
输出:[1,1,3]
解释:每个盒子对应的最小操作数如下:
- 第 1 个盒子:将一个小球从第 2 个盒子移动到第 1 个盒子,需要 1 步操作。
- 第 2 个盒子:将一个小球从第 1 个盒子移动到第 2 个盒子,需要 1 步操作。
- 第 3 个盒子:将一个小球从第 1 个盒子移动到第 3 个盒子,需要 2 步操作。将一个小球从第 2 个盒子移动到第 3 个盒子,需要 1 步操作。共计 3 步操作。
示例 2:
输入:boxes = “001011”
输出:[11,8,5,4,3,4]
提示:
n == boxes.length
1 <= n <= 2000
boxes[i] 为 ‘0’ 或 ‘1’
分析:
先初始化一个返回的数组,数组的元素都置为0
int* answer=(int*)malloc(sizeof(int)*n);
for(int s=0;s<n;s++)
{
answer[s]=0;
}
比如,下面是3个盒子,第一个盒子有1个球,第二个盒子有1个球,第3个盒子有0个球
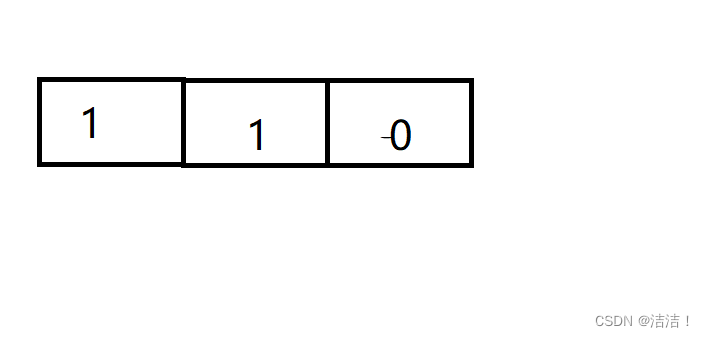
第一次,把第二个盒子的1个球移到第一个盒子里面,共要移动一次,第3个盒子没有,所以不用移动。
第二次,把第一个盒子的1个球移到第二个盒子里,移动一次,第3个盒子没有,所以也不要移动。
第三次,把第一个盒子的1个球移动到第3个盒子里,要移动2次,把第2个盒子的1个球移动到第3个盒子,要移动1次,总共移动3次。
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(boxes[j]=='1')
{
int num=0;
num=num+sqrt((j-i)*(j-i));
answer[i]=answer[i]+num;
}
}
}
if(boxes[j]=='1')这里是要判断一下,盒子里面是否有球
num=num+sqrt((j-i)*(j-i));防止出现负数 (j-i)有可能小于0
经过次代码之后,answer数组就已经是我们想要的答案了。
代码实现:
/ * Note: The returned array must be malloced, assume caller calls free().
*/
int* minOperations(char * boxes, int* returnSize){
int n = strlen(boxes);
int* answer=(int*)malloc(sizeof(int)*n);
for(int s=0;s<n;s++)
{
answer[s]=0;
}
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(boxes[j]=='1')
{
int num=0;
num=num+sqrt((j-i)*(j-i));
answer[i]=answer[i]+num;
}
}
}
*returnSize=n;
return answer;
}