【数据结构】二叉树的实现

news2024/11/26 2:24:18

文章目录

  • 一、二叉树的概念
  • 二、特殊的二叉树
  • 三、二叉树的性质
  • 四、二叉树的存储结构
  • 五、二叉树链式结构实现
    • （1）创建结构体
    • （2）具体函数实现及实现
      • 1.0 二叉树的构建
      • 1.1 二叉树的销毁
      • 1.2 二叉树节点个数
      • 1.3 二叉树叶子结点个数
      • 1.4 二叉树第k层节点个数
      • 1.5 二叉树查找值为x的节点
      • 1.6 二叉树的高度
      • 1.7 二叉树前序遍历
      • 1.8 二叉树中序遍历
      • 1.9 二叉树后序遍历
      • 2.0 层序遍历
      • 2.1 判断二叉树是否是完全二叉树
    • （3）二叉树实现代码
      • （1）Queue.c
      • （2）Queue.h
      • （3）test.c
      • （4）BinaryTree.h
      • （5）BinaryTree.c
    • （4）二叉树测试结果

一、二叉树的概念

一棵二叉树是结点的一个有限集合，该集合分为两点: 一是为空和二是由一个根节点加上两棵别称为左子树和右子树的二叉树组成从图上看出有2个性质：

  1. 二叉树不存在度大于2的结点
  2. 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树
    在这里插入图片描述

对于任意的二叉树都是由以下几种情况复合而成的：
在这里插入图片描述

二、特殊的二叉树

1、 满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是 说，如果一个二叉树的层数为K，且结点总数是 ，则它就是满二叉树。

2、完全二叉树：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K 的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。

如图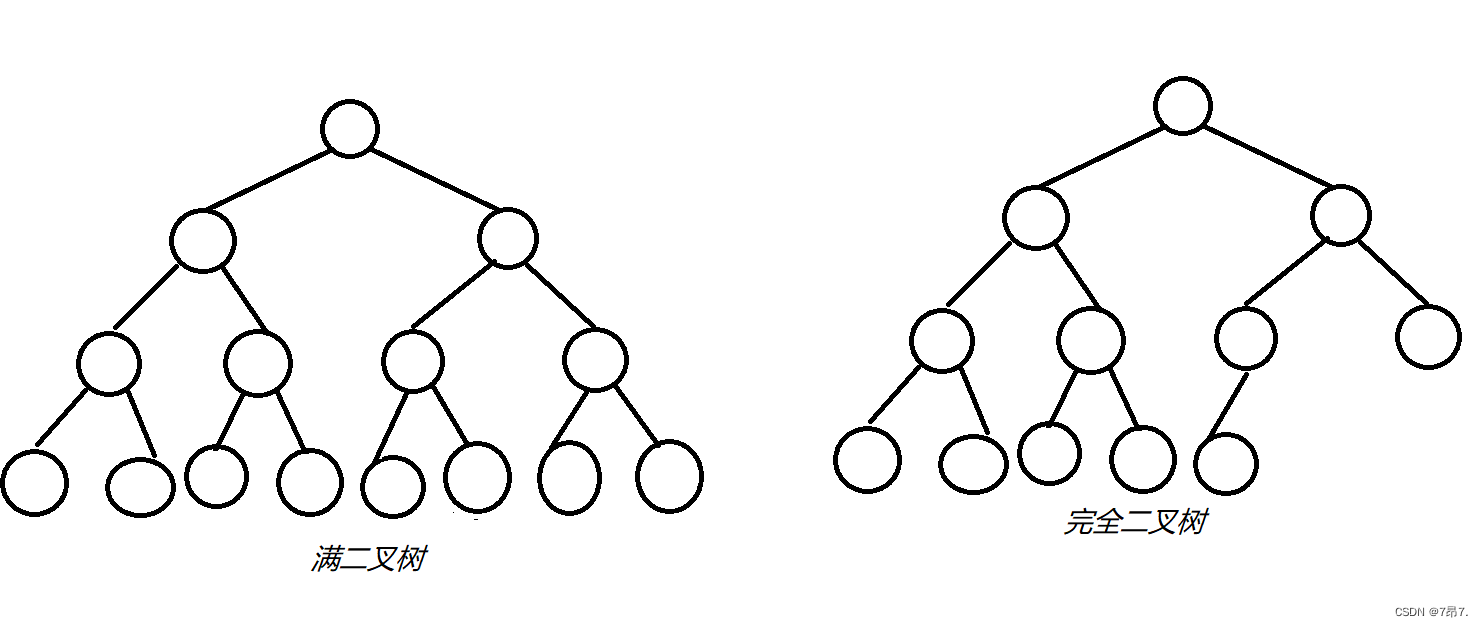：在这里插入图片描述

三、二叉树的性质

二叉树数的性质有五点：

  1. 若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有2^(i-1) 个结点.
  2. 若规定根节点的层数为1，则深度为h的二叉树的最大结点数是 2^h-1
  3. 对任何一棵二叉树, 如果度为0其叶结点个数为n0 , 度为2的分支结点个数为n2 ,则有 n0＝n2 ＋1
  4. 若规定根节点的层数为1，具有n个结点的满二叉树的深度，h=log(n+1) ( 是log以2 为底，n+1为对数)
  5. 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，则对 于序号为i的结点有:
    若i>0，i位置节点的双亲序号：(i-1)/2；i=0，i为根节点编号，无双亲节点
    若2i+1<n，左孩子序号：2i+1，2i+1>=n否则无左孩子
    若2i+2<n，右孩子序号：2i+2，2i+2>=n否则无右孩子

四、二叉树的存储结构

二叉树一般可以使用两种结构存储，一种顺序结构，一种链式结构。
1、顺序存储：
顺序结构存储就是使用数组来存储，一般使用数组只适合表示完全二叉树，因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树。
在这里插入图片描述
2、链式存储
二叉树的链式存储结构：是用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链，这只讲二叉链。
在这里插入图片描述

五、二叉树链式结构实现

（1）创建结构体


typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

先使用typedef int BTDataType,是为了方便改类型，在结构体里创建3个成员变量，BTDataType a，表示结点数据。struct BinaryTreeNode* left表示存储结点左孩子的地址，struct BinaryTreeNode* right表示存储结点右孩子的地址。

（2）具体函数实现及实现

1.0 二叉树的构建

BTNode* BuyBTNode(BTDataType x)//二叉树的构建
{
	 BTNode* node = (struct BTNode*) malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	node->data = x;
	node->left = NULL;
	node->right = NULL;
	return node;
}

二叉树构建也就是为每一个结点申请空间，用malloc开辟，地址放在node变量中，如果改指针为空就exit,接着把数据值放到结点数据里，把2它的左右孩子都置为空。

1.1 二叉树的销毁

void BinaryTreeDestory(BTNode* root)//二叉树的销毁
{
	if (root)
	{
		BinaryTreeDestory(root->left);
		BinaryTreeDestory(root->right);
		free(root);
	}

}

二叉树销毁根节点为空就不用销毁，反之，先递归释放左子树，再递归释放右子树，最后释放结点，如果先释放结点，会找不到左右子树的地址。

1.2 二叉树节点个数


int BinaryTreeSize(BTNode* root)// 二叉树节点个数
{
	if (root == NULL)
	{
		return 0;
	}
	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;

}

求二叉树结点个数需要递归左子树和右子树，去建立栈帧，直到它们的子树为空返回0，之后再加1，表示记录一个结点，然后从下到上开始return返回，栈帧逐层销毁，最终返回结点个数。

1.3 二叉树叶子结点个数

int BinaryTreeLeafSize(BTNode* root)//二叉树叶子结点个数
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left==NULL&&root->right == NULL)
	{
		return 1;
	}
	return  BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

求叶子结点个数，也就是求同时没有左右孩子的结点，思路还是递归左子树和右子树，之和即为最终的叶子节点个数。如果结点为空直接返回0，如果它们的左右孩子都为空，则表示它是叶子结点，返回1，最后递归返回总个数。

1.4 二叉树第k层节点个数

int BinaryTreeLevelKSize(BTNode* root, int k)// 二叉树第k层节点个数
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

求第k层个数，从二叉树结构可以发现，如果k=1，他自己就是第k层，如果k>1,第k层就等于左子树k-1层个数加右子树第k-1层个数，相对位置往下走，层层递进，一直减到1，就是第k层。同样递归左右子树，最后返回最终第k层结点个数。

1.5 二叉树查找值为x的节点

struct BinaryTreeNode* BinaryTreeFind(BTNode* root, BTDataType x)// 二叉树查找值为x的节点
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	struct BinaryTreeNode* ret1 = BinaryTreeFind(root->left, x);
	if (ret1)
		return ret1;
	struct BinaryTreeNode* ret2 = BinaryTreeFind(root->right, x);
	if (ret2)
		return ret2;
	
}

二叉树查找，如果结点为空，返回空，如果找到直接返回结点指针，没找到继续分别递归左右子树，为了防止返回出现随机值，这里需要接收一下指针，如果找到返回该结点指针。

1.6 二叉树的高度

int BinaryTreeHeight(BTNode* root)//二叉树的高度
{
	if (root == NULL)
	{
		return 0;
	}
	int leftheight = BinaryTreeHeight(root->left);
	int rightheight = BinaryTreeHeight(root->right);
	return leftheight > rightheight ? leftheight + 1:rightheight + 1;

}

求二叉树高度思路把问题还是分解为子问题，结点高度等于左子树高度和右子树高度大的那个一个加1，因为高度是最长的那条路径，分别递归左子树和右子树去比较，如果都为0，任取一个加1。最终返回最终高度。

1.7 二叉树前序遍历

void BinaryTreePrevOrder(BTNode* root)// 二叉树前序遍历 
{
	if (root == NULL)
	{
	
		printf("NULL ");
		return;
	}
	printf("%d ", root->data);
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
}

前序遍历更为简单，如果为空直接返回，接着打印根数据，再递归左子树，再递归右子树。

1.8 二叉树中序遍历

void BinaryTreeInOrder(BTNode* root)// 二叉树中序遍历
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	BinaryTreeInOrder(root->left);
	printf("%d ", root->data);
	BinaryTreeInOrder(root->right);
}

中序遍历，如果为空直接返回，先递归左子树，再打印根数据，再递归右子树。

1.9 二叉树后序遍历

void BinaryTreePostOrder(BTNode* root)// 二叉树后序遍历
{
	if (root == NULL)
	{
		
		printf("NULL ");
		return;
	}
	BinaryTreePostOrder(root->left);
	BinaryTreePostOrder(root->right);
	printf("%d ", root->data);
}

中序遍历，如果为空直接返回，先递归左子树，再打印根数据，再递归右子树。

2.0 层序遍历

void BinaryTreeLevelOrder(BTNode* root)// 层序遍历
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		printf("%d ", front->data);
		QueuePop(&q);
		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	printf("\n");
	QueueDestroy(&q);
}

层序遍历在这用队列去实现，队列里面存地址。如果根节点不为空，就先把这个结点地址导入进去。之后用while循环来控制终止，队列不为空就进去，然后先把上次导入进去的队列头部数据保存起来放到front指针变量，便于删除在队列里删除它，还不影响导入它的左右孩子，左右孩子不为空则导入。最后释放队列。

2.1 判断二叉树是否是完全二叉树

bool BinaryTreeComplete(BTNode* root)// 判断二叉树是否是完全二叉树
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front == NULL)
		{
			break;
		}
		else
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
	}
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true;

}

判断是否是完全二叉树的思路：是同样是用队列去实现，如果从队列出，遇到结点为空，就去判断后面的是否为空，后面只要出现一个非空就不是完全二叉树，后面全为空就是二叉树。
1、如果根结点不为空，就先导入队列中，接着同样是用while循环，里面是导入数据即结点地址，先把队列头保存起来，再pop掉，if语句为真，停止，说明遇到空了，否则继续导入数据包括空也导入进去。
2、接着再用whil循环，出到空后，继续往后出数。只要找到一个非空就返回false，直到循环结束，返回真，说明都是空。

（3）二叉树实现代码

（1）Queue.c

#include"Queue.h"
void QueueInit(Queue* qq)//队列初始化
{
	assert(qq);
	qq->head = qq->tail = NULL;
	qq->size = 0;

}

void QueuePush(Queue* qq, QDataType x)//入队列
{
	assert(qq);
    QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
	}
	newnode->data = x;
	newnode->next = NULL;
	if (qq->tail == NULL)
	{
		qq->head = qq->tail = newnode;
	}
	else
	{
		qq->tail->next = newnode;
		qq->tail = qq->tail->next;
	}
	qq->size++;
}

void QueuePop(Queue* qq)//出队列
{
	assert(qq);
	assert(!QueueEmpty(qq));
	if (qq->head->next == NULL)
	{
		free(qq->head);
		qq->head = qq->tail = NULL;
	}
	else
	{
		QNode* del = qq->head;
		qq->head = qq->head->next;
		free(del);
	}
	qq->size--;
	
}

QDataType QueueFront(Queue* qq)//取队列首元素
{
	assert(qq);
	assert(!QueueEmpty(qq));
	return qq->head->data;


}

QDataType QueueBack(Queue* qq)//取队列尾元素
{
	assert(qq);
	assert(!QueueEmpty(qq));
	return qq->tail->data;

}

int QueueSize(Queue* qq)//返回队列个数
{
	assert(qq);
	return qq->size;
}

bool QueueEmpty(Queue* qq)//判断是否为空
{
	assert(qq);
	return qq->head == NULL &&qq->tail == NULL;

}

void QueueDestroy(Queue* qq)//销毁队列
{
	assert(qq);
	QNode* cur = qq->head;
	while (cur)
	{
		QNode* del = cur;
		cur = cur->next;
		free(del);
	}
	qq->head = qq->tail = NULL;
	qq->size = 0;
}

（2）Queue.h

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

struct BinaryTreeNode;
typedef struct BinaryTreeNode* QDataType;

typedef struct QueueNode
{
	QDataType data;
	struct QueueNode* next;
}QNode;
typedef struct Queue
{
	QNode* head;
	QNode* tail;
	int size;
}Queue;
void QueueInit(Queue* qq);//队列初始化

void QueuePush(Queue* qq,QDataType x);//入队列

void QueuePop(Queue* qq);//出队列

QDataType QueueFront(Queue* qq);//取队列首元素

QDataType QueueBack(Queue* qq);//取队列尾元素

int QueueSize(Queue* qq);//返回队列个数

bool QueueEmpty(Queue* qq);//判断是否为空

void QueueDestroy(Queue* qq);//销毁队列

（3）test.c

#include"BinaryTree.h"
int main()
{
	BTNode* n1 = BuyBTNode(1);
	BTNode* n2 = BuyBTNode(2);
	BTNode* n3 = BuyBTNode(3);
	BTNode* n4 = BuyBTNode(4);
	BTNode* n5 = BuyBTNode(5);
	BTNode* n6 = BuyBTNode(6);
	BTNode* n7 = BuyBTNode(7);

	n2->right = n7;
	n1->left = n2;
	n1->right = n4;
	n2->left = n3;
	n4->left = n5;
	n4->right = n6;

	BinaryTreePrevOrder(n1);//前序遍历
	printf("\n");

	BinaryTreeInOrder(n1);//中序遍历
	printf("\n");

	BinaryTreePostOrder(n1);//后序遍历
	printf("\n");

	printf("TreeSize:%d\n", BinaryTreeSize(n1));
	printf("TreeLeafSize:%d\n", BinaryTreeLeafSize(n1));
	printf("TreeHeight:%d\n", BinaryTreeHeight(n1));
	printf("TreeKLevelSize:%d\n", BinaryTreeLevelKSize(n1, 3));
	printf("TreeFind:%p\n", BinaryTreeFind(n1, 7));

	BinaryTreeLevelOrder(n1);

	return 0;
	
}

（4）BinaryTree.h

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

#include"Queue.h"

BTNode* BuyBTNode(BTDataType x);//二叉树的构建

void BinaryTreeDestory(BTNode** root);//二叉树的销毁

int BinaryTreeSize(BTNode* root);// 二叉树节点个数

int BinaryTreeLeafSize(BTNode* root);//二叉树叶子结点个数

int BinaryTreeLevelKSize(BTNode* root, int k);// 二叉树第k层节点个数

BTNode* BinaryTreeFind(BTNode* root, BTDataType x);// 二叉树查找值为x的节点

int BinaryTreeHeight(BTNode* root);//二叉树的高度

void BinaryTreePrevOrder(BTNode* root);// 二叉树前序遍历 

void BinaryTreeInOrder(BTNode* root);// 二叉树中序遍历

void BinaryTreePostOrder(BTNode* root);// 二叉树后序遍历

void BinaryTreeLevelOrder(BTNode* root);// 层序遍历

bool BinaryTreeComplete(BTNode* root);// 判断二叉树是否是完全二叉树

（5）BinaryTree.c

#include"BinaryTree.h"

BTNode* BuyBTNode(BTDataType x)//二叉树的构建
{
	 BTNode* node = (struct BTNode*) malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	node->data = x;
	node->left = NULL;
	node->right = NULL;
	return node;
}

void BinaryTreeDestory(BTNode* root)//二叉树的销毁
{
	if (root)
	{
		BinaryTreeDestory(root->left);
		BinaryTreeDestory(root->right);
		free(root);
	}

}

int BinaryTreeSize(BTNode* root)// 二叉树节点个数
{
	if (root == NULL)
	{
		return 0;
	}
	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;

}

int BinaryTreeLeafSize(BTNode* root)//二叉树叶子结点个数
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left==NULL&&root->right == NULL)
	{
		return 1;
	}
	return  BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

int BinaryTreeLevelKSize(BTNode* root, int k)// 二叉树第k层节点个数
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

struct BinaryTreeNode* BinaryTreeFind(BTNode* root, BTDataType x)// 二叉树查找值为x的节点
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	struct BinaryTreeNode* ret1 = BinaryTreeFind(root->left, x);
	if (ret1)
		return ret1;
	struct BinaryTreeNode* ret2 = BinaryTreeFind(root->right, x);
	if (ret2)
		return ret2;
	
}

int BinaryTreeHeight(BTNode* root)//二叉树的高度
{
	if (root == NULL)
	{
		return 0;
	}
	int leftheight = BinaryTreeHeight(root->left);
	int rightheight = BinaryTreeHeight(root->right);
	return leftheight > rightheight ? leftheight + 1:rightheight + 1;

}

void BinaryTreePrevOrder(BTNode* root)// 二叉树前序遍历 
{
	if (root == NULL)
	{
	
		printf("NULL ");
		return;
	}
	printf("%d ", root->data);
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
}

void BinaryTreeInOrder(BTNode* root)// 二叉树中序遍历
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	BinaryTreeInOrder(root->left);
	printf("%d ", root->data);
	BinaryTreeInOrder(root->right);
}

void BinaryTreePostOrder(BTNode* root)// 二叉树后序遍历
{
	if (root == NULL)
	{
		
		printf("NULL ");
		return;
	}
	BinaryTreePostOrder(root->left);
	BinaryTreePostOrder(root->right);
	printf("%d ", root->data);
}

void BinaryTreeLevelOrder(BTNode* root)// 层序遍历
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		printf("%d ", front->data);
		QueuePop(&q);
		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	printf("\n");
	QueueDestroy(&q);
}

bool BinaryTreeComplete(BTNode* root)// 判断二叉树是否是完全二叉树
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front == NULL)
		{
			break;
		}
		else
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
	}
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true;

}

（4）二叉树测试结果

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/50462.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【Pandas数据处理100例】（九十）：Pandas使用period_range()生成固定间隔日期

【Pandas数据处理100例】（九十）：Pandas使用period_range()生成固定间隔日期

前言 大家好，我是阿光。 本专栏整理了《Pandas数据分析处理》，内包含了各种常见的数据处理，以及Pandas内置函数的使用方法，帮助我们快速便捷的处理表格数据。 正在更新中~ ✨ 🚨 我的项目环境： 平台：Windows10语言环境：python3.7编译器：PyCharmPandas版本：1.3.5N…
阅读更多...
【自然语言处理概述】99乘法表

【自然语言处理概述】99乘法表

【自然语言处理&#xff08;NLP&#xff09;】99乘法表 作者简介&#xff1a;在校大学生一枚&#xff0c;华为云享专家&#xff0c;阿里云专家博主&#xff0c;腾云先锋&#xff08;TDP&#xff09;成员&#xff0c;云曦智划项目总负责人&#xff0c;全国高等学校计算机教学与产…
阅读更多...
量子计算（十）：量子计算原理

量子计算（十）：量子计算原理

文章目录 量子计算原理 一、酉变换 二、矩阵的指数函数 三、单位矩阵 四、单量子比特逻辑门 五、泡利矩阵 六、常见逻辑门 量子计算原理 经典计算中&#xff0c;最基本的单元是比特&#xff0c;而最基本的控制模式是逻辑门&#xff0c;可以通过逻辑门的组合来达到控制电…
阅读更多...
[附源码]Python计算机毕业设计SSM课堂考勤（程序+LW)

[附源码]Python计算机毕业设计SSM课堂考勤（程序+LW)

项目运行 环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; SSM mybatis Maven Vue 等等组成&#xff0c;B/S模式 M…
阅读更多...
【C++】vector的认识+模拟实现

【C++】vector的认识+模拟实现

目录1️⃣vector的概念2️⃣STL中vector的使用2.1 vector的定义2.2 iterator的使用2.3 vector的空间问题2.4 vector的增删查改2.5 迭代器失效问题2.5.1 什么是迭代器&#xff1f;2.5.2 迭代器失效3️⃣vector的模拟实现3.1 迭代器3.2 构造函数&#x1f50e;memcpy的拷贝异常问题…
阅读更多...
【Java面试】为什么重写equals方法必须同时重写HashCode方法？

【Java面试】为什么重写equals方法必须同时重写HashCode方法？

众所周知再JDK1.8之后&#xff0c;Java修改了String类型的底层源码&#xff0c;因为他们发现其实对于-128~127范围的字符更加常用&#xff0c;因此将底层的数组从char类型修改为了byte类型。 看到上面的方法可以发现&#xff0c;String类型的equals方法会先比较两个字符串的…
阅读更多...
Caffeine 源码、架构、原理（史上最全，10W字 超级长文）

Caffeine 源码、架构、原理（史上最全，10W字 超级长文）

文章很长&#xff0c;而且持续更新&#xff0c;建议收藏起来&#xff0c;慢慢读&#xff01;疯狂创客圈总目录 博客园版 为您奉上珍贵的学习资源 &#xff1a; 免费赠送 :《尼恩Java面试宝典》 持续更新 史上最全 面试必备 2000页 面试必备 大厂必备 涨薪必备 免费赠送 经典…
阅读更多...
软件实训-技术学习心得

软件实训-技术学习心得

一、MoOtA 前端主要负责动态界面的编写&#xff0c;主要学习JavaScript&#xff0c;HTML&#xff0c;CSS三件套 1、前端项目文件夹 .idea&#xff1a;无需关注 node_modules&#xff1a;无需关注 public&#xff1a;存放媒体资源&#xff0c;比如图片&#xff08;images&…
阅读更多...
CSS网页页面图像灰色滤镜写法示例

CSS网页页面图像灰色滤镜写法示例

阿酷TONY / 原创 2022-12-1 / 长沙 / grayscale()函数是一个内置函数&#xff0c;用于对图像应用滤镜以设置图像的灰度。 用法: grayscale( amount ) 参数&#xff1a;此函数接受包含灰度值的单个参数量。灰度值根据数量和百分比设置。值0&#xff05;表示原始图像&…
阅读更多...
Java并发编程—Thread类中的start()方法如何启动一个线程？

Java并发编程—Thread类中的start()方法如何启动一个线程？

一、java线程的介绍&#xff1a; 在java的开发过程中&#xff0c;很多铁子对于java线程肯定不感到陌生&#xff0c;作为java里面重要的组成部分&#xff0c;这里就从如何创建一个线程给大家进行分析&#xff1b; 二、相关知识引入&#xff1a; ​ 之前我了解过&#xff0c;j…
阅读更多...
jQuery 简介

jQuery 简介

jQuery 库可以通过一行简单的标记被添加到网页中。 您需要具备的基础知识 在您开始学习 jQuery 之前&#xff0c;您应该对以下知识有基本的了解&#xff1a; HTMLCSSJavaScript 如果您需要首先学习这些科目&#xff0c;请在我们的 首页 查找这些教程。 什么是 jQuery &#x…
阅读更多...
[附源码]Python计算机毕业设计Django的高校资源共享平台

[附源码]Python计算机毕业设计Django的高校资源共享平台

项目运行 环境配置&#xff1a; Pychram社区版 python3.7.7 Mysql5.7 HBuilderXlist pipNavicat11Djangonodejs。 项目技术&#xff1a; django python Vue 等等组成&#xff0c;B/S模式 pychram管理等等。 环境需要 1.运行环境&#xff1a;最好是python3.7.7&#xff0c;…
阅读更多...
无人机机械臂爪机器臂爪的安装调试试验。以大疆哪吒为例乐迪T8Fb遥控器。

无人机机械臂爪机器臂爪的安装调试试验。以大疆哪吒为例乐迪T8Fb遥控器。

首先将机械爪安装完毕。注意不要装的太紧&#xff0c;否则会损害舵机&#xff0c;应力度合适&#xff0c;可以先使用舵机测试仪测试。 安装舵机到位。要使用机械爪配套的舵机型号&#xff0c;否则孔位对不上。 调整螺丝孔位&#xff0c;确保齿轮能够吻合。 调整螺丝松紧&#…
阅读更多...
JavaScript 基础笔记

JavaScript 基础笔记

初识 JavaScript JavaScript负责页面中的的行为&#xff0c;是一门运行在客户端的脚本语言。 解释型语言与编译型语言区别&#xff1a; JavaScript 作用 表单动态校验&#xff08;密码校验&#xff09;网页特效服务端开发桌面端开发等作用 JS引擎&#xff1a;浏览器使用Js引…
阅读更多...
Vue3多个弹窗同时出现解决思路

Vue3多个弹窗同时出现解决思路

Vue3多个弹窗同时出现解决思路 弹窗或者说对话框是我们在开发系统或者页面很常用的元素&#xff0c;所以博主想对出现多个弹窗的情况下的解决思路进行一个整理 有时候我们一个页面可能存在多个弹窗&#xff0c;当多个弹窗出现的时候可能屏幕就变的很黑&#xff0c;如下图所示…
阅读更多...
图观引擎V3.3.4 功能更强、操作更便捷！最新升级一睹为快

图观引擎V3.3.4 功能更强、操作更便捷！最新升级一睹为快

图观™引擎&#xff0c;自去年内测版推出上线以来&#xff0c;已帮助众多合作伙伴开发出自己的数字孪生应用、落地交付数字孪生项目&#xff0c;实现了自身软件产品的全面升级、技术能力的大幅拓展。 经过不断的升级迭代&#xff0c;图观™引擎V3.3.4版本&#xff0c;更加注重…
阅读更多...
Seata中TC服务部署及微服务集成Seata

Seata中TC服务部署及微服务集成Seata

seata的部署和集成 一、部署Seata的tc-server 1.下载 首先我们要下载seata-server包&#xff0c;地址在http&#x1f615;/seata.io/zh-cn/blog/download.html 2.解压 在非中文目录解压缩这个zip包&#xff0c;其目录结构如下&#xff1a; 3.修改配置 修改conf目录下的re…
阅读更多...
微服务框架 SpringCloud微服务架构 8 Gateway 网关 8.1 网关作用介绍

微服务框架 SpringCloud微服务架构 8 Gateway 网关 8.1 网关作用介绍

微服务框架 【SpringCloudRabbitMQDockerRedis搜索分布式&#xff0c;系统详解springcloud微服务技术栈课程|黑马程序员Java微服务】 SpringCloud微服务架构 文章目录微服务框架SpringCloud微服务架构8 Gateway 网关8.1 网关作用介绍8.1.1 为什么需要网关8.1.2 网关的技术实现…
阅读更多...
高数 | 周洋鑫 冲刺预测题自用整理复习

高数 | 周洋鑫 冲刺预测题自用整理复习

自用笔记整理复习。 内容来自2023周洋鑫冲刺班。 加油ヾ(◍∇◍)ﾉﾞ 1、函数极限计算 【加项减项】 ☆ 二次积分求极限
阅读更多...
极值分析：分块极大值BLOCK-MAXIMA、阈值超额法、广义帕累托分布GPD拟合降雨数据时间序列...

极值分析：分块极大值BLOCK-MAXIMA、阈值超额法、广义帕累托分布GPD拟合降雨数据时间序列...

全文链接&#xff1a;http://tecdat.cn/?p25348 你们可能知道&#xff0c;实际极值分析有两种常用方法&#xff1a;分块极大值Block-maxima、阈值超额法threshold excess&#xff08;点击文末“阅读原文”获取完整代码数据&#xff09;。今天&#xff0c;我们将分别介绍这两种…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023