本文以求解整数规划模型为例，提供分支定界算法的 Python 代码框架，期待完善、指正和交流。

文件结构

具体代码

problem.py

定义问题的格式：

from typing import List


class Problem(object):
    """
    problem
    """
    def __init__(self, problem_type: str, 
                 num_var: int, mat_cons: List[List[int or float]], obj_coef: List[int or float]) -> None:
        """
        initialise
        
        :param problem_type:  problem type
        :param num_var:  number of variables
        :param mat_cons:  constraint coefficients matrix
        :param obj_coef:  objective coefficients list
        """

        self.problem_type = problem_type
        
        self.num_var = num_var
        self.mat_cons = mat_cons
        self.obj_coef = obj_coef

solver.py

定义问题求解模块的基类：

from algorithm.problem import Problem


class Solver(object):
    """
    problem solver
    """
    def __init__(self, problem: Problem) -> None:
        """
        initialise
        
        :param problem:  problem to solve
        """
        
        self.num_var = problem.num_var
        self.mat_cons = problem.mat_cons
        self.obj_coef = problem.obj_coef

        # solution status
        self.status = 'empty'  # {'empty', 'invalid', 'optimal', 'feasible', 'infeasible', 'fail'}
        self.obj = None
        self.solution = []

    def _is_valid(self) -> bool:
        return True

    def solve(self):
        pass

solver_lp.py

继承求解模块基类，针对线性规划问题，编写调用 OR-Tools GLOP 求解器的求解模块子类：

from datetime import datetime

import rich
from ortools.linear_solver import pywraplp

from config import ACCURACY
from algorithm.solver import Solver
from algorithm.problem import Problem


class SolverLP(Solver):
    """
    problem solver, LP model
    """
    def __init__(self, problem: Problem) -> None:
        """
        initialise
        
        :param problem:  problem to solve
        """

        super().__init__(problem)

    def _is_valid(self) -> bool:
        """
        check model format

        :return:  if model valid
        """

        # constraint coefficient lists
        for i in range(len(self.mat_cons)):
            cons = self.mat_cons[i]

            # coefficients list length
            if len(cons) != self.num_var + 2:
                rich.print(f"Constraint {i} length {len(cons)} invalid, need to be {self.num_var} + 2")
                return False
            
        # objective coefficients list length
        if len(self.obj_coef) != self.num_var + 1:
            rich.print(
                f"Objective coefficients list length {len(self.obj_coef)} invalid, need to be {self.num_var} + 1")
            return False
        
        return True

    def solve(self):
        """
        solving
        """

        if not self._is_valid():
            self.status = 'invalid'
            return
        
        solver = pywraplp.Solver("lp", problem_type=pywraplp.Solver.GLOP_LINEAR_PROGRAMMING)
        
        x = [solver.NumVar(0, solver.infinity(), 'x_{}'.format(i)) for i in range(self.num_var)]

        # constraints
        for cons in self.mat_cons:
            exp = 0
            for j in range(len(cons[: -2])):
                exp += cons[j] * x[j]
            sign, b = cons[-2], cons[-1]
            
            # index -2 coefficient: negative for <=; 0 for ==; positive for >=
            if sign < 0:
                solver.Add(exp <= b)
            elif sign == 0:
                solver.Add(exp == b)
            else:
                solver.Add(exp >= b)

        # objective
        obj = 0
        for j in range(len(self.obj_coef[: -1])):
            obj += self.obj_coef[j] * x[j]
        # index -1 coefficient: positive for maximise; otherwise minimise
        solver.Minimize(obj) if self.obj_coef[-1] <= 0 else solver.Maximize(obj)

        # solve
        dts = datetime.now()
        status = solver.Solve()
        dte = datetime.now()
        tm = round((dte - dts).seconds + (dte - dts).microseconds / (10 ** 6), 3)
        rich.print(f"LP model solving time:  {tm} s")

        # result
        if status == pywraplp.Solver.OPTIMAL:
            self.status = 'optimal'
            self.obj = solver.Objective().Value()
            self.solution = [x[i].solution_value() for i in range(self.num_var)]
            rich.print(f"objective value:  {self.obj}")
            rich.print(f"solution:  {[round(x, ACCURACY) for x in self.solution]}")
        elif status == pywraplp.Solver.FEASIBLE:
            self.status = 'feasible'
            rich.print(f"Didn't get an optimal solution, but a feasible one.")
        elif status == pywraplp.Solver.INFEASIBLE:
            self.status = 'infeasible'
            rich.print(f"The problem does not have a feasible solution.")
        else:
            self.status = 'fail'
            rich.print(f"Failed to solving problem for an unknown reason.")

node.py

分支定界算法的节点模块：

from typing import List
import copy

from config import PROBLEM_TYPES, INSTANCE, ACCURACY
from algorithm.problem import Problem
from algorithm.solver_lp import SolverLP


class Node(object):
    """
    branch and bound node
    """
    def __init__(self, id: int, father: int or None, new_cons: List[int or float]) -> None:
        """
        initialise
        
        :param id:  node ID
        :param father:  father node ID, None for root
        :param id:  new constraits other than father node's constraints
        """

        self.problem: Problem = copy.deepcopy(INSTANCE)
        self.problem_type = self.problem.problem_type
        self.num_var, self.mat_cons, self.obj_coef = self.problem.num_var, self.problem.mat_cons, self.problem.obj_coef
        
        # check problem type
        if self.problem_type not in PROBLEM_TYPES:
            raise Exception(f"Problem type {self.problem_type} invalid!")
        
        self.id = id

        self.father = father
        self.new_cons = new_cons

        self.depth = None

        # solution
        self.status = 'empty'  # {'empty', 'feasible', 'relax', 'infeasible'}
        self.obj = None
        self.solution = []
        self.infeasible_list = []

    def add_ancestor_cons(self, ancestor_cons: List[List[int or float]]):
        """
        initialise
        
        :param ancestor_cons:  constraints from ancestors
        """

        self.mat_cons += ancestor_cons

    def solve(self):
        """
        solve problem
        """

        # add new constraint
        if self.new_cons:
            self.mat_cons.append(self.new_cons)

        solver = SolverLP(problem=self.problem)
        solver.solve()

        status, self.obj, self.solution = solver.status, solver.obj, solver.solution
        if status in {'optimal', 'feasible'}:
            self._check_solution()
            self.status = 'feasible' if not self.infeasible_list else 'relax'
        else:
            self.status = 'infeasible'

    def _check_solution(self):
        """
        check if solution valid
        """

        if self.problem_type == 'IP':
            self._check_integer()
        else:
            pass

    def _check_integer(self):
        """
        check if all solutions are integers
        """

        for i in range(len(self.solution)):
            x = self.solution[i]
            if round(x, ACCURACY) != round(x):
                self.infeasible_list.append((i, x))

algorithm.py

分支定界算法的算法模块，要点：

• 每得到一个可行解，更新最优可行解（incumbent）
• 每完成一次分支（所有子节点求解完毕），更新全局的界（bound）
  
  

import datetime
from typing import List, Dict
import math

import rich

from config import PROBLEM_TYPES, INSTANCE, ACCURACY
from algorithm.problem import Problem
from algorithm.node import Node


class BranchAndBound(object):
    """
    branch and bound algorithm
    """
    def __init__(self, time_limit: int or float = 3600, gap_upper: float = 0) -> None:
        """
        initialise
        
        :param time_limit:  time limit of solving
        :param gap_upper:  upper bound of gap of solving
        """

        self.problem: Problem = INSTANCE
        self.problem_type = self.problem.problem_type
        self.num_var, self.mat_cons, self.obj_coef = self.problem.num_var, self.problem.mat_cons, self.problem.obj_coef
        
        # check problem type
        if self.problem_type not in PROBLEM_TYPES:
            raise Exception(f"Problem type {self.problem_type} invalid!")

        # optimising direction
        self.opt_dir = 'min' if self.obj_coef[-1] <= 0 else 'max'

        # solving params
        self.time_limit = time_limit
        self.gap_upper = gap_upper
        self.dt_start, self.dt_end = datetime.datetime.now(), None
        self.final_time_cost = None
        self.final_gap = None

        # nodes
        self.idx_acc = 0
        self.nodes: Dict[int, Node] = {}  # all nodes, key: ID
        self.leaf_nodes: List[int] = []  # node ID

        # solution status
        self.status = 'empty'  # {'empty', 'optimal', 'feasible', 'infeasible', 'fail'}
        self.solution = None
        self.incumbent, self.incumbent_node = None, None  # update once feasible solution found
        self.bound, self.bound_node = None, None  # update once leaf nodes updated

    @property
    def time_cost(self) -> float:
        """
        get time cost
        """

        dt_end = datetime.datetime.now()
        tm_delta: datetime.timedelta = dt_end - self.dt_start
        return round(tm_delta.seconds + tm_delta.microseconds / 1e6, 6)

    @property
    def reach_time_limit(self) -> bool:
        """
        check if reach time limit
        """

        return self.time_cost >= self.time_limit
    
    @property
    def gap(self) -> bool:
        """
        calculate current gap
        """

        # case 1: searched all nodes
        if self.bound_node not in self.leaf_nodes:
            return 0
        
        # case 2: catched both incumbent and bound
        elif self.bound is not None and self.incumbent is not None:
            return abs(self.bound - self.incumbent) / abs(self.incumbent)
        
        else:
            return None
    
    @property
    def reach_accuracy(self) -> bool:
        """
        check if gap reach accuracy
        """

        return True if self.gap is not None and self.gap <= self.gap_upper else False

    def run(self):
        """
        algorithm main process
        """

        self.dt_start = datetime.datetime.now()

        # root node and solve
        node_index = self.idx_acc
        self.idx_acc += 1
        node = Node(id=node_index, father=None, new_cons=[])
        node.depth = 0
        self.nodes[node_index] = node
        rich.print(f"Solving node {node_index}")
        node.solve()

        # special case 1: root node feasible
        if node.status == 'feasible':
            self.solution = node.solution
            self.status = 'optimal'
            return

        # special case 2: root node infeasible
        elif node.status == 'infeasible':
            self.status = 'infeasible'
            return
        
        # update leaf nodes and bound
        self.leaf_nodes.append(node.id)
        self._update_bound()
        rich.print()

        # main circulation
        node_index = self._select_node()
        while node_index is not None:  # attention: don't use "while node_index" because the index can be 0
            # branch and get new leaf nodes
            is_terminated = self._branch(node_index=node_index)

            # check termination
            if is_terminated:
                self.final_time_cost = self.time_cost
                self.final_gap = self.gap
                rich.print(f"final time cost:  {self.final_time_cost}")
                rich.print(f"final gap:  {self.final_gap}")
                return

            # select node to branch
            node_index = self._select_node()
            rich.print()

        # all nodes searched
        self.final_gap = self.gap
        if self.incumbent_node is not None:
            self.solution = self.nodes[self.incumbent_node].solution
            self.status = 'optimal' if self.final_gap == 0 else 'feasible'
        else:
            self.status = 'ineasible'
        self.final_time_cost = self.time_cost
        rich.print(f"final time cost:  {round(self.final_time_cost, 3)} s")
        rich.print(f"final gap:  {self.final_gap}")
        rich.print(f"total nodes:  {len(self.nodes)}")
        rich.print(f"maximal node depth:  {max(self.nodes[i].depth for i in self.nodes)}")
        rich.print()

    def _select_node(self) -> int or None:  # TODO: node selection strategy: bound node
        """
        node selection

        :return:  selected node index
        """

        # have updated bound before
        return self.bound_node if self.bound_node in self.leaf_nodes else None

    def _branch(self, node_index: int) -> bool:
        """
        branching
        
        :param node_index:  father node index

        :return:  if algorithm terminates
        """

        node = self.nodes[node_index]

        list_new_cons = self._get_new_constraints(node_index=node_index)
        for cons in list_new_cons:
            # new node
            node_index_new = self.idx_acc
            self.idx_acc += 1
            node_new = Node(id=node_index_new, father=node.id, new_cons=cons)
            node_new.depth = node.depth + 1
            self.nodes[node_index_new] = node_new

            # inherit constraints from ancestors
            ancestor_cons = []
            node_new_ = node_new
            while node_new_.father:
                ancestor_cons.append(self.nodes[node_new_.father].new_cons)
                node_new_ = self.nodes[node_new_.father]
            node_new.add_ancestor_cons(ancestor_cons=ancestor_cons)

            # solve node and check incumbent
            rich.print(f"Solving node {node_index_new}")
            rich.print(f"new constraint coefficients:  {cons}")
            node_new.solve()
            rich.print(f"node status:  {node_new.status}")
            if node_new.status == 'feasible':
                incumbent_updated = self._update_incumbent(feasible_node=node_index_new)
                
                # update incumbent and check accuracy
                if incumbent_updated:
                    if self.reach_accuracy:
                        rich.print(
                            f"Gap {self.gap} reach accuracy {self.gap_upper}, bound {round(self.bound, ACCURACY)}")

                        self.solution = self.nodes[self.incumbent_node].solution
                        self.status = 'optimal' if self.gap == 0 else 'feasible'
                        return True
                
            # check time limit
            if self.reach_time_limit:
                rich.print(f"Time limit reached!")

                if self.incumbent_node is not None:
                    self.solution = self.nodes[self.incumbent_node].solution
                    self.status = 'optimal' if self.gap == 0 else 'feasible'
                else:
                    rich.print(f"Didn't find a feasible solution within time limit!")
                    self.status = 'fail'

                return True
                
            # add new leaf node
            if node_new.status == 'relax':
                self.leaf_nodes.append(node_index_new)
            rich.print()
                
        # remove old leaf node
        self.leaf_nodes.remove(node_index)
        
        # update bound and check accuracy
        bound_updated = self._update_bound()
        if bound_updated:
            if self.reach_accuracy:
                rich.print(
                    f"Gap {self.gap} reach accuracy {self.gap_upper}, incumbent {round(self.incumbent, ACCURACY)}")
                rich.print()

                self.solution = self.nodes[self.incumbent_node].solution
                self.status = 'optimal' if self.gap == 0 else 'feasible'

                return True

        return False

    def _get_new_constraints(self, node_index: int) -> List[List[float or int]]:  # TODO: branching strategy: index-based
        """
        get new constraints for node branching
        
        :param node_index:  branching node

        :return:  new constraints list
        """

        node = self.nodes[node_index]

        if self.problem_type == 'IP':
            idx_infeasible, infeasible_solution = node.infeasible_list[0]
            new_cons_1 = [1 if i == idx_infeasible else 0 for i in range(self.num_var)] + [
                -1, math.floor(infeasible_solution)]
            new_cons_2 = [1 if i == idx_infeasible else 0 for i in range(self.num_var)] + [
                1, math.ceil(infeasible_solution)]

            return [new_cons_1, new_cons_2]

        else:
            pass

    def _update_incumbent(self, feasible_node: int) -> bool:
        """
        update global feasible solution
        
        :param feasible_node:  index of new feasible node

        :return:  if incumbent updated
        """

        node = self.nodes[feasible_node]

        # get a feasible solution firstly
        if self.incumbent is None:
            self.incumbent, self.incumbent_node = node.obj, feasible_node
            rich.print(f"Get new incumbent {round(self.incumbent, ACCURACY)} from node {self.incumbent_node}")
            return True
        
        # get a better feasible solution
        elif (self.opt_dir == 'min' and node.obj < self.incumbent) or (
            self.opt_dir == 'max' and node.obj > self.incumbent):
            self.incumbent, self.incumbent_node = node.obj, feasible_node
            rich.print(f"Get new incumbent {round(self.incumbent, ACCURACY)} from node {self.incumbent_node}")
            return True
        
        return False
    
    def _update_bound(self) -> bool:
        """
        update global bound

        :return:  if bound updated
        """

        bound, bound_node = None, None
        for node_idx in self.leaf_nodes:
            node = self.nodes[node_idx]
            if node.status == 'relax':
                if bound is None:
                    bound, bound_node = node.obj, node_idx
                elif (self.opt_dir == 'min' and node.obj < bound) or (
                    self.opt_dir == 'max' and node.obj > bound):
                    bound, bound_node = node.obj, node_idx

        if bound is not None:
            self.bound, self.bound_node = bound, bound_node
            rich.print(f"Get new bound {round(self.bound, ACCURACY)} from node {self.bound_node}")
            return True
        
        return False

cases.py

基于前面定义的问题格式，提供两个整数规划算例：

一个简单算例：

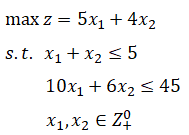
一个 NP 算例：
分支定界算法的 NP 算例

from algorithm.problem import Problem


CASES = {}


"""
IP: simple
"""

num_var = 2
mat_cons = [
    [1, 1, -1, 5], 
    [10, 6, -1, 45]
]
var_range = [
    [1, 0, 1, 0], 
    [0, 1, 1, 0]
]
mat_cons += var_range
obj_coef = [5, 4, 1]

CASES['IP-simple'] = Problem(problem_type='IP', num_var=num_var, mat_cons=mat_cons, obj_coef=obj_coef)


"""
IP: NP-hard
"""

num_var = 16
mat_cons = [[2 for _ in range(num_var - 1)] + [1] + [0] + [15]]
var_range = [
    [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] + [1] + [0], 
    [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] + [1] + [0], 
    [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] + [1] + [0], 
    [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] + [1] + [0], 
    [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] + [1] + [0], 
    [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] + [1] + [0], 
    [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0] + [1] + [0], 
    [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0] + [1] + [0], 
    [0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0] + [1] + [0], 
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0] + [1] + [0], 
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0] + [1] + [0], 
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0] + [1] + [0], 
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0] + [1] + [0], 
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0] + [1] + [0], 
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0] + [1] + [0], 
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1] + [1] + [0], 
    [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] + [-1] + [1], 
    [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] + [-1] + [1], 
    [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] + [-1] + [1], 
    [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] + [-1] + [1], 
    [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] + [-1] + [1], 
    [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] + [-1] + [1], 
    [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0] + [-1] + [1], 
    [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0] + [-1] + [1], 
    [0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0] + [-1] + [1], 
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0] + [-1] + [1], 
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0] + [-1] + [1], 
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0] + [-1] + [1], 
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0] + [-1] + [1], 
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0] + [-1] + [1], 
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0] + [-1] + [1], 
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1] + [-1] + [1],
]
mat_cons += var_range
obj_coef = [0 for _ in range(num_var - 1)] + [1] + [-1]

CASES['IP-NP-hard'] = Problem(problem_type='IP', num_var=num_var, mat_cons=mat_cons, obj_coef=obj_coef)

config.py

根目录下的配置文件，含算例选取、算法精确度等全局变量：

from algorithm.cases import CASES


PROBLEM_TYPES = {'IP'}  # TODO: only support IP model so far

# INSTANCE = CASES['IP-simple']
INSTANCE = CASES['IP-NP-hard']

ACCURACY = 3  # 0.001

main.py

主程序：

import rich

from config import ACCURACY
from algorithm.algorithm import BranchAndBound


rich.print()
branch_and_bound = BranchAndBound(time_limit=300, gap_upper=0)
branch_and_bound.run()

status = branch_and_bound.status
solution = [round(x, ACCURACY) for x in branch_and_bound.solution]
optimal_obj = branch_and_bound.incumbent
rich.print(f"algorithm final status:  {status}")
rich.print(f"algorithm final solution:  {solution}")
rich.print(f"algorithm final objective value:  {optimal_obj}")
rich.print()

算例运行效果

简单算例

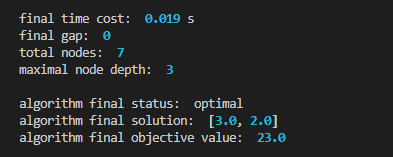
NP 算例

展望

本文原本致力于写一个朴素的适用于各类问题的分支定界算法框架，其实也就是玩玩，但由于精力有限，只完成了求解整数规划问题的部分，并且算法内部的具体策略较为简单，因此对更多的功能实现做出一点展望，期望完善、指正和交流：

• 更丰富的分支策略：本文代码选用所有不可行约束中序号最小的进行分支
• 更丰富的节点选择策略：本文代码选择了叶子节点中的界（bound）节点进行下一深度的搜索
• 更夫妇的问题类型：如使用分支定界算法求解 TSP、CBS（conflict-based search）、branch-and-price 等问题，当然，当前框架不一定可行或合理，期待更好的实现方法
• 引入有效割：提升算法性能