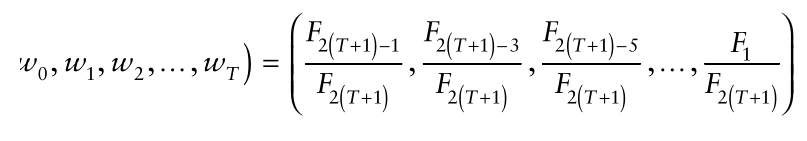本文是Quantitative Methods and Analysis: Pairs Trading此书的读书笔记。
估计一个常数的通常做法是,做多次测量(measurement),然后使用测量的平均值作为估计值。从统计学的思想上来说,这种做法可以尽量减小估计的误差。这种方法需要等到所有个测量都完成了才能进行估计。而卡尔曼滤波器则是基于当前可用信息对常数的值进行估计,并在进行更多观测(observation)时更新估计。
注意,如果不同的观测值的误差方差(error variance)是一样的,使用求平均值的方法是没问题的。然而,在观测值具有不同精度水平的情况下,我们希望给更高精度的观测值分配更多的权重,在这种情况下,用加权平均是更好的方法。而卡尔曼滤波器可以解决加权平均情况,这涉及到对卡尔曼增益(Kalman gain)的计算。
在估计一个常数值的情形下,系统状态就是一维的常数本身。现在用表示对常数值的预测,预测的误差表示为
。

其中是常数的真实值。尽管我们不知道
是多少,但是我们知道它服从均值为0,方差为
的分布。
现在我们开始预测步骤。因为这个值是常数,我们对于下一个状态的预测就是当前值本身,即
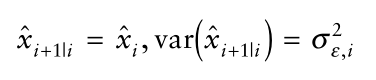
接下来,我们做测量(measurement或者说观测),常数的观测值为,观测误差
服从均值为零,方差为
的分布。在测量步骤结束的时候,我们有观测值(observation),

我们有了预测值和观测值,接下来就是协调这两个值。也就是到了修正的步骤了,使用观测值去修正预测值,修正的结果为:
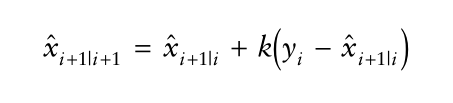
进一步调整修正值的式子:
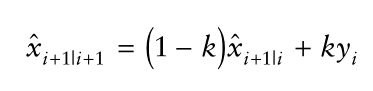
也就是修正状态是两种值的加权平均数。这个权重就是卡尔曼增益Kalman gain。
我们需要找到这个最小化最终状态估计值的误差方差(error variance),或者说最小化以下式子:
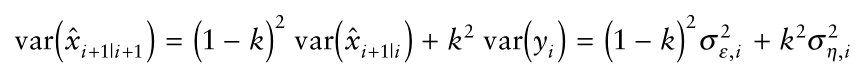
这里,我们不使用求导数的方式去获得最佳的值。我们会通过电路理论(circuit theory)去获得
值。
现在看一个图:
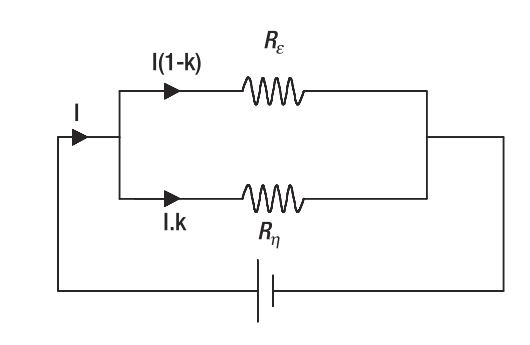
电流以比重和
流经两个分支。根据欧姆定律,电流量跟这个分支的电阻是呈反比的。根据基尔霍夫定律,总的电流量就是每个分支的电流量之和
。电流在流动的过程中会让消耗的能量最小。能量的消耗表示为:
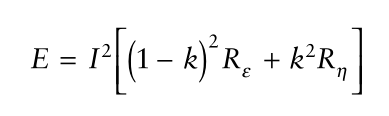
让=
,
=
,这样这个式子跟最终估计值的方差就建立了联系了。最佳卡尔曼增益
就是:
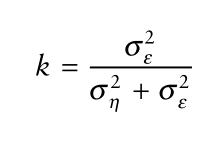
这样在最佳卡尔曼增益下,得到电路的有效电阻或方差为:
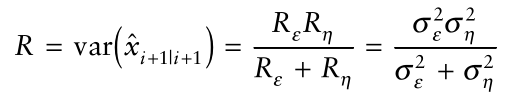
确定了的值后,我们现在可以计算修正状态和修正状态的方差。现在,在下一次测量中再次重复该过程,直到我们到达计划的n次测量中的最后一次。
在进行所有测量后,取加权平均值的最终结果将会跟使用卡尔曼滤波计算得到的值是相同的。



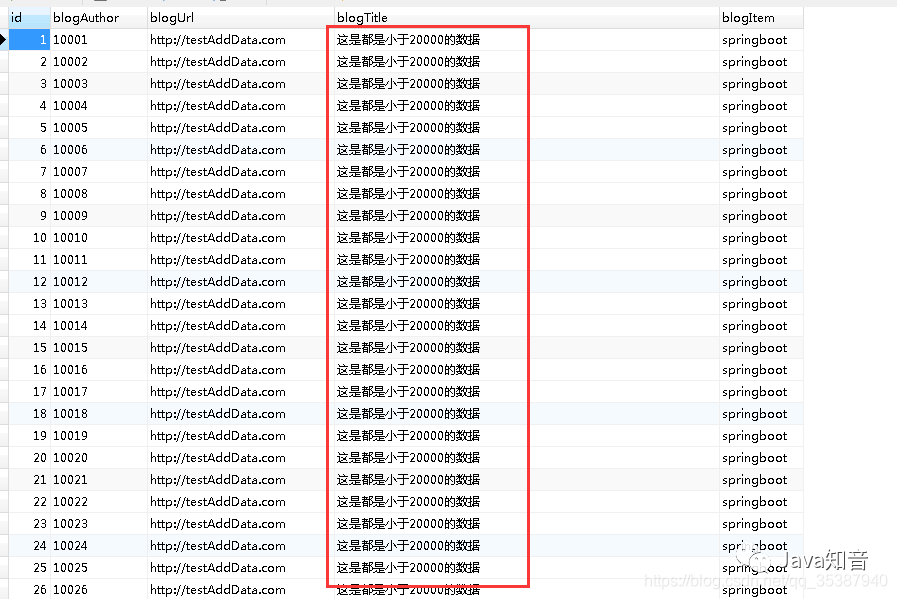
![[附源码]Python计算机毕业设计Django房产中介管理系统](https://img-blog.csdnimg.cn/92fcfebc94f34686920f9fd90a5164e9.png)
![[附源码]计算机毕业设计springboot路政管理信息系统](https://img-blog.csdnimg.cn/32cf592261904523843dd7c8525ee211.png)


![[附源码]Python计算机毕业设计SSM辽宁科技大学二手车交易平台(程序+LW)](https://img-blog.csdnimg.cn/05f51247fafc41f7b459d329a0613e80.png)