Java高阶数据结构 并查集 最小生成树

news2024/10/7 8:30:32

并查集与最小生成树


文章目录

  • Java高阶数据结构 & 并查集 & 最小生成树
    • 1. 并查集
      • 1.1 并查集的原理
        • 1.1.1 例子：
        • 1.1.2 这样存储有什么好处呢？
      • 1.2 并查集的代码实现
        • 1.2.1 类的定义与属性
        • 1.2.2 构造方法
        • 1.2.3 获取下标的方法
        • 1.2.4 获得根节点
        • 1.2.5 两个节点建立联系
        • 1.2.6 判断两个节点是否在一个集合内
        • 1.2.7 计算集合的个数
        • 1.2.8 打印并查集
      • 1.3 并查集的应用
        • 1.3.1 省份的数量
        • 1.3.2 等式方程的可满足性
        • 1.3.3 Kruskal算法获取图的最小生成树
    • 2. 图的最小生成树问题
      • 2.1 生成树是什么
      • 2.2 获取最小生成树算法
        • 2.2.1 Kruskal算法
        • 2.2.2 Prime算法
      • 2.3 获取最小生成树代码实现
        • 2.3.1 Kruskal算法代码实现（邻接矩阵）
        • 2.3.2 Prime算法代码实现（邻接矩阵）

Java高阶数据结构 & 并查集 & 最小生成树

1. 并查集

1.1 并查集的原理

在一些应用问题中，我们常常会遇到一类问题

一开始是一个人

  1. 后来新增的人可能与这个人有关系，也可能与这个人无关系。
  2. 一个人与一个人有关系，这个人与另一个人也有关系，那么三人都有关系。
  3. 有关系的和没关系的之间是不同的类别。

在这里插入图片描述

  • 而随着人数增加，有多少类别是不确定的，所以用普通的二维数组是很难描述和存储这种数据结构的。
  • 因为即使在不考虑时间复杂度的情况下，我们不知道有多少行，并且出现“三人都有关系”的情况的时候，需要合并等等…

而现在有一种数据结构，就专门去解决这个问题，这就是**“并查集”**

需要将n个不同的元素划分成一些不相交的集合。

开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。

在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-find set)

（先说怎么存储表示的，再说如何构建）

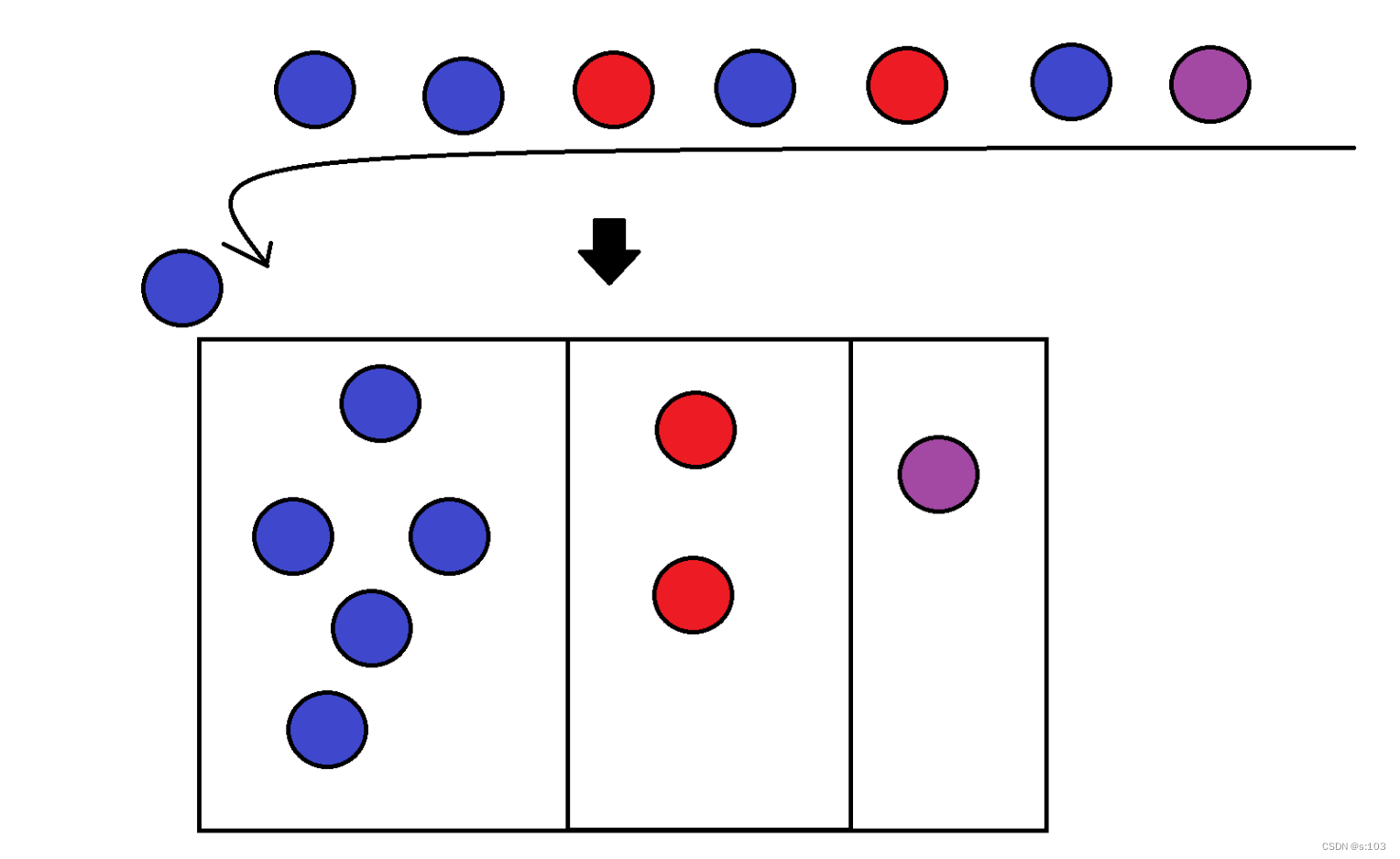
并查集是一个int型的一维数组，而本质就是一维顺序表存储的“森林”

有如下特性：

  1. 每个节点都有对应的下标，如果有n个节点，那么他们就对应数组的0-n-1
  2. 森林的不同的树，代表不同的类别
  3. 每棵树都有一个根节点，这个根节点在数组中的值为负数，绝对值为这棵树节点的个数
  4. 每棵树的非根节点在数组中的值为其父节点在数组中的下标

1.1.1 例子：

  • 现在有十个人，他们分别代表0 - 9
  • 他们原本互不相识，但是今天是他们因为缘分出现在同一辆公交车上，这次行程他们都很长，并且在路上网络全无，他们也毫无困意，并且都是社牛。

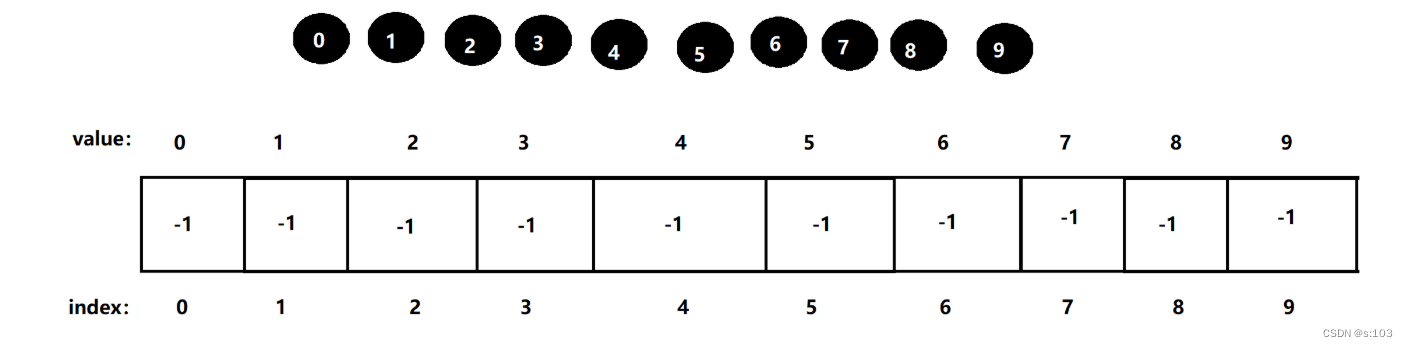
在这里插入图片描述

  • 他们开始与周围的车友交谈，可能因为各种原因，如兴趣爱好和地域性，他们互相交换了微信。如果两个人同时与一个人交换微信，那么这两个人也会获得对方的微信。
  • 最终下电梯，他们的朋友圈是这样的：
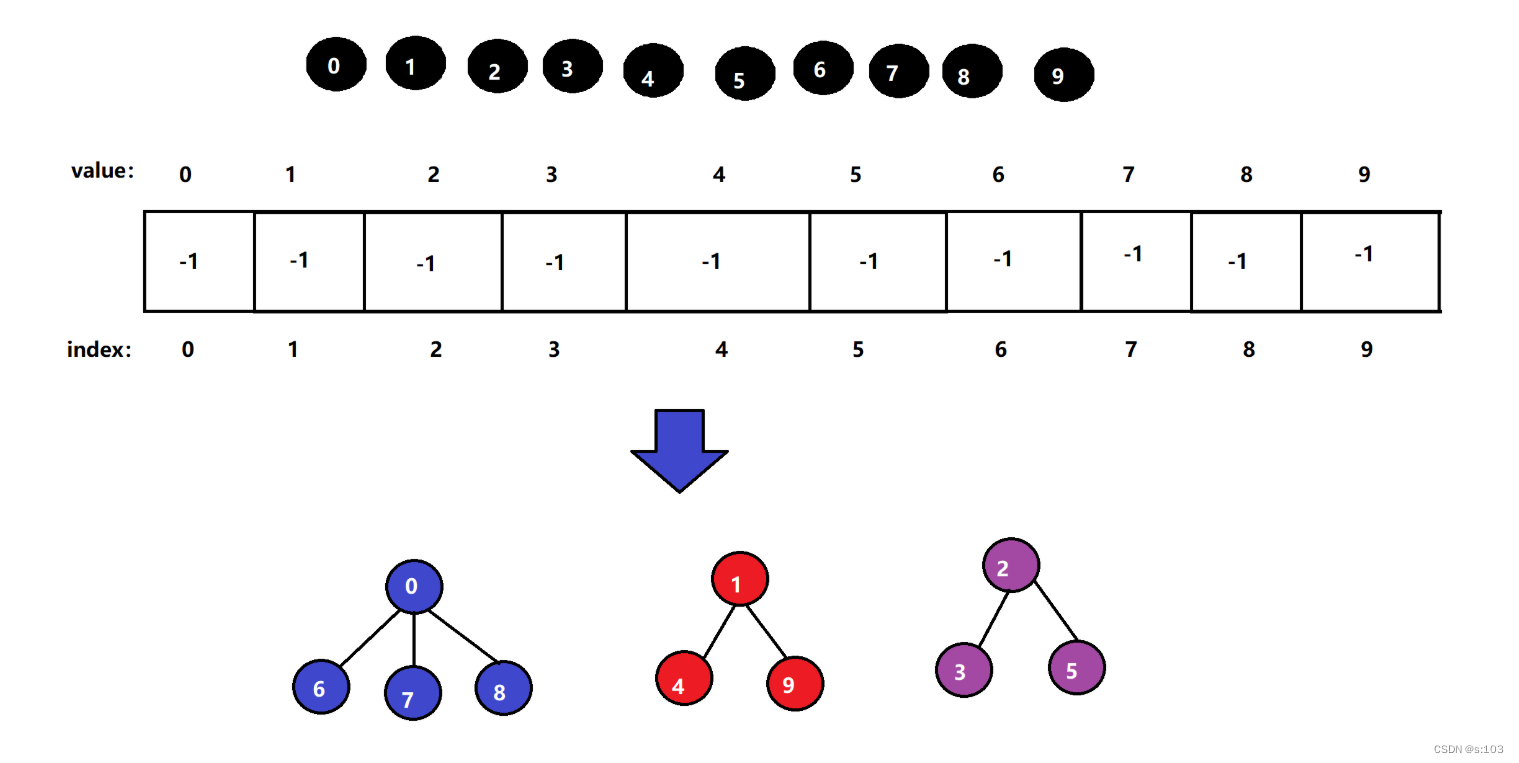
    在这里插入图片描述

而并查集将变成这样：

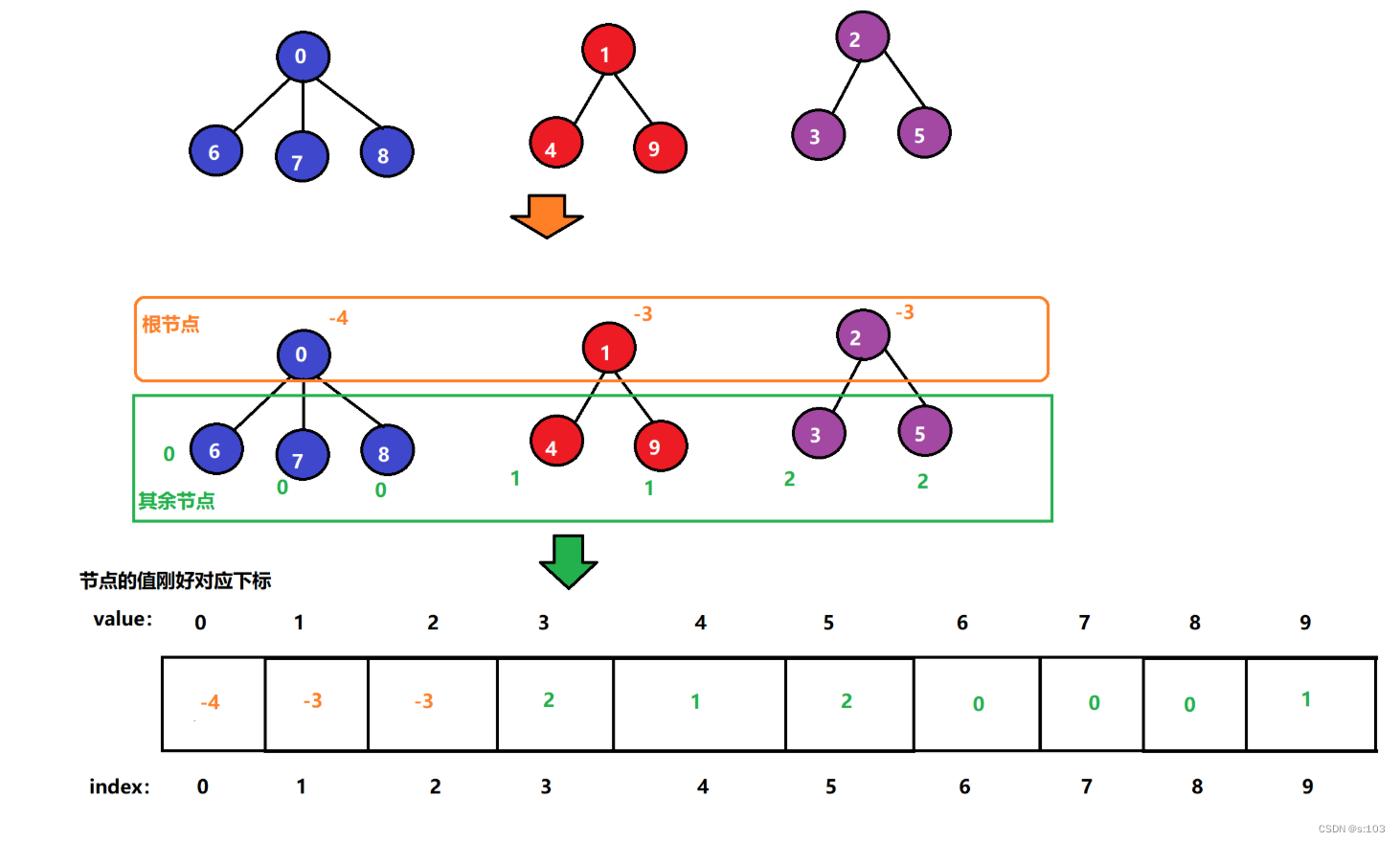
在这里插入图片描述

1.1.2 这样存储有什么好处呢？

如果有n个节点，那么一开始分为n个类别

如果a0与a1有关系，那么只需要让a0和a1其中一棵树根节点接到另一棵树的根节点即可

  1. 一棵树的根节点的值对于新的树的节点数的负数
  2. 另一棵树的根节点变为“新树的非根节点”，其值为根节点的下标

通过这个机制，最终会很好的分好类别，不需要分好组让把他们放进去，而是他们自己分好了

  • 因为同一棵树的根节点都一样，所以负数值的元素有多少个，就说明有多少组
  • 当然所有非根节点都可以压缩其值为其所在数的根节点对应下标

而判断两个节点有没有关系，就只需要判断他们根节点是否相同即可

1.2 并查集的代码实现

了解完机制之后，并查集的代码实现并不复杂！

1.2.1 类的定义与属性

public class UnionFindSet {
    private int[] elem;
}

这就是并查集的主体

1.2.2 构造方法

public UnionFindSet(int n) {
    this.elem = new int[n];
    Arrays.fill(this.elem, -1);
}
  • 根据n构造数组，并且利用fill充满数组为-1

1.2.3 获取下标的方法

//根据需求得到下标
public int getIndexByX(int x) {
    return x;
}
  • 这个需要根据实际需求
  • 一般x与i是一致的
    • 或者是x = ki + b（k属于整数）
    • 对于其他特殊情况，你需要给每个节点安排下标
  • 这一点只需要在传参的时候转化为下标即可

下面的代码都是认为传参的就是下标

1.2.4 获得根节点

public int findRoot(int x) {
    if(x < 0) {
        throw new IndexOutOfBoundsException("下标为负数");
    }
    while(elem[x] >= 0) {
        x = elem[x];
    }
    return x;
}
  • 如果是压缩后的并查集,直接返回elem[x]即可
  • 如果不是，这需要溯源到根节点

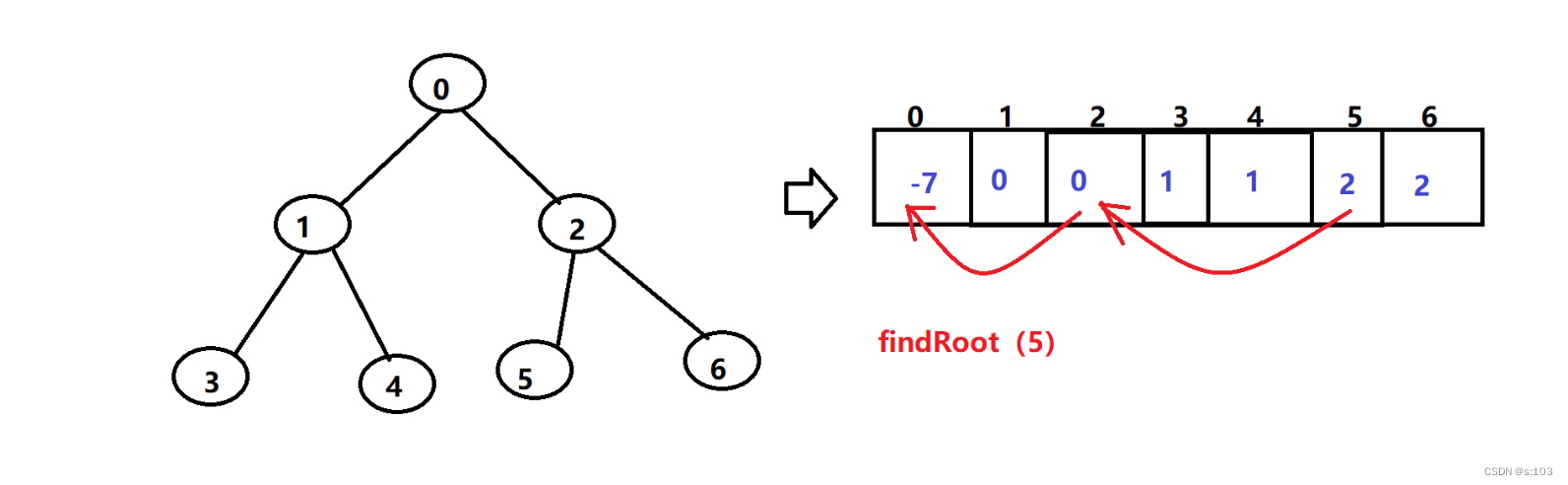
在这里插入图片描述

1.2.5 两个节点建立联系

  • 只要两个节点来自不同的树，那么就可以建立联系，即两个集合合并
  • 如果来自同一棵树，什么也不做

注意：这里你可以选择x1合并x2，或者x2合并x1

//合并x1和x2
//设x1任然是根节点，x2连接到x1下
public void union(int x1, int x2) {
    int index1 = findRoot(x1);
    int index2 = findRoot(x2);
    if(index1 == index2) {
        return;//同一棵树
    }else {
        elem[index1] += elem[index2];
        elem[index2] = index1;
    }
}

例子：

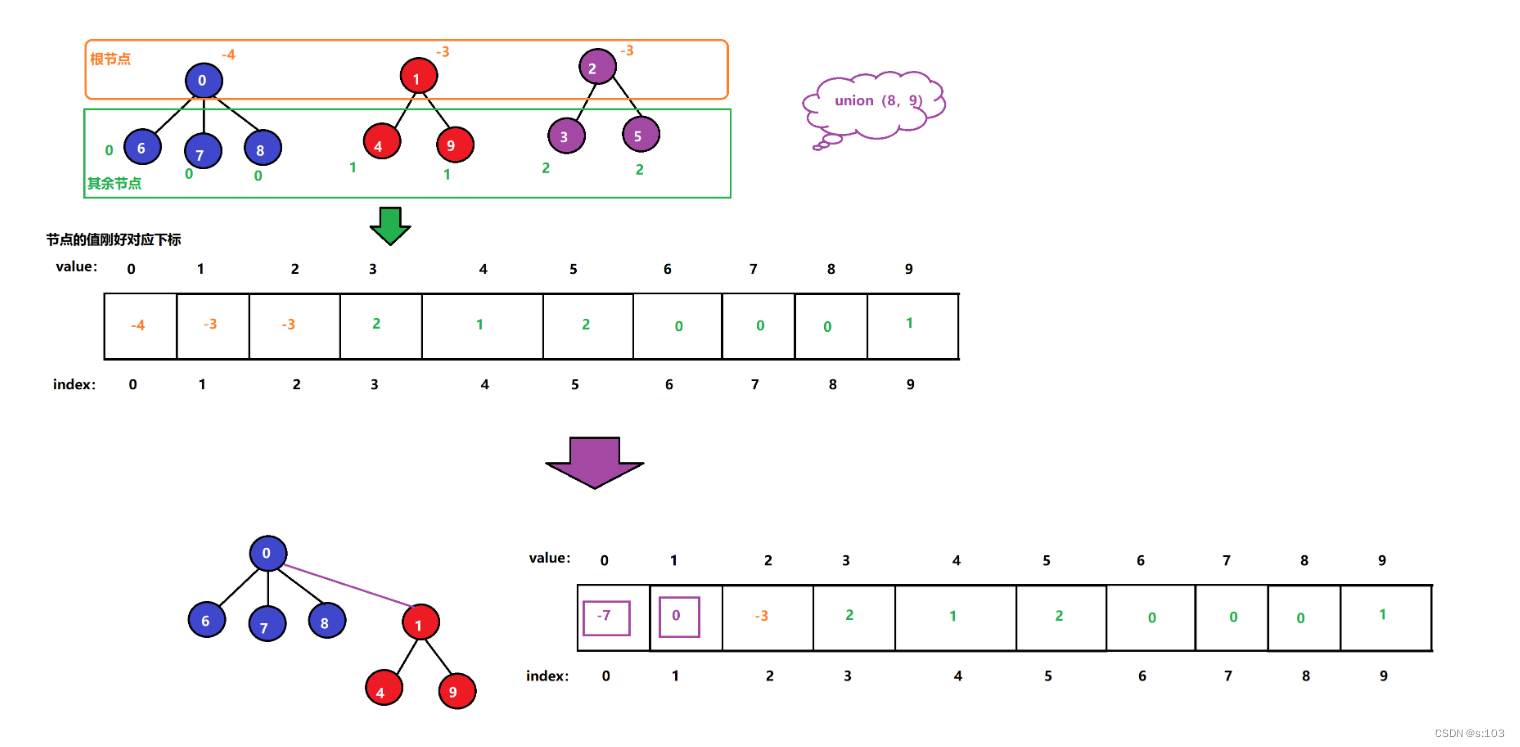
在这里插入图片描述

1.2.6 判断两个节点是否在一个集合内

//判断是否在一个集合内
public boolean isSameSet(int x1, int x2) {
    return findRoot(x1) == findRoot(x2);
}

1.2.7 计算集合的个数

//计算集合的个数
public int getSetCount() {
    int count = 0;
    for(int x : elem) {
        if(x < 0) {
            count++;
        }
    }
    return count;
}

1.2.8 打印并查集

public void display() {
    for(int x : elem) {
        System.out.print(x + " ");
    }
    System.out.println();
}

1.3 并查集的应用

1.3.1 省份的数量

力扣547

在这里插入图片描述

是不是一模一样，^ v ^

分析：

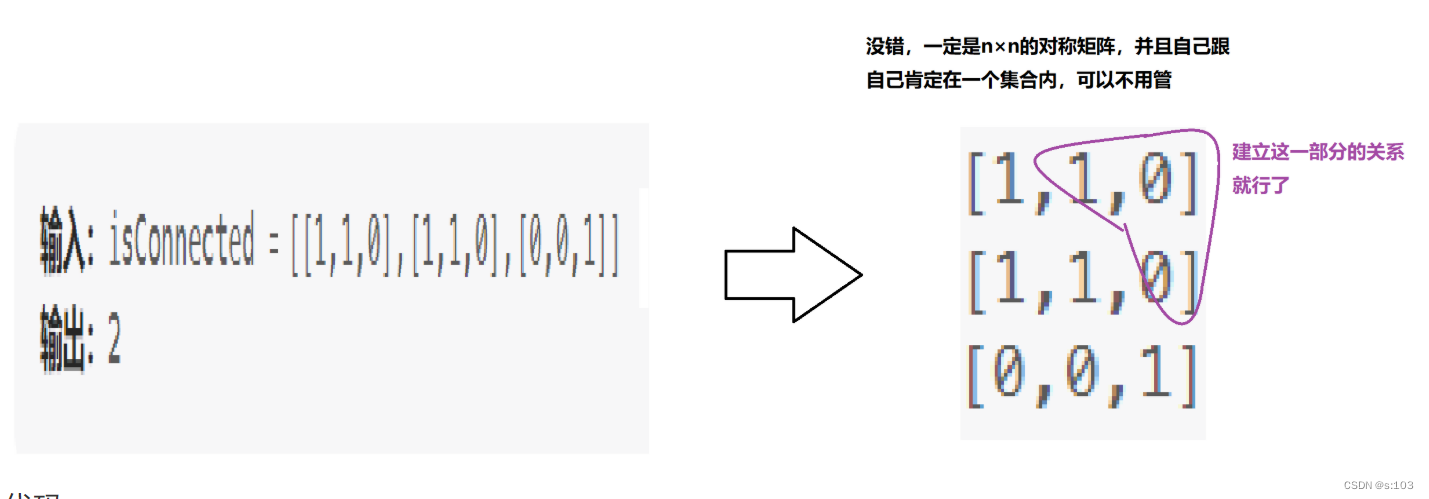
在这里插入图片描述

代码：

//获得省份数量
public int findCircleNum(int[][] isConnected) {
    int n = isConnected.length;
    UnionFindSet unionFindSet = new UnionFindSet(n);
    for (int i = 0; i < n; i++) {
        for (int j = i + 1; j < n; j++) {
            if(isConnected[i][j] == 1) {
                unionFindSet.union(i, j);
            }
        }
    }
    return unionFindSet.getSetCount();
}

在这里插入图片描述

1.3.2 等式方程的可满足性

力扣990

在这里插入图片描述

分析：

思路：

  1. 区分不同的字符串种类（等于号类和不等号类）
  2. 通过等号类构建并查集
  3. 通过不等号类去检查是否合理
//下标转化方法（这道题节点最多26个，因为只能是不重复的小写字母）
public int getIndexByX(char x) {
    return x - 'a';
}
//等式方程可满足性

public boolean equationsPossible(String[] equations) {
    UnionFindSet unionFindSet = new UnionFindSet(26);
    for(String str : equations) {
        if(str.charAt(1) == '=') {
            char ch1 = str.charAt(0);
            char ch2 = str.charAt(3);
            unionFindSet.union(getIndexByX(ch1), getIndexByX(ch2));
        }
    }
    for(String str : equations) {
        if(str.charAt(1) == '!') {
            char ch1 = str.charAt(0);
            char ch2 = str.charAt(3);
            if(unionFindSet.isSameSet(getIndexByX(ch1), getIndexByX(ch2))) {
                return false;
            }
        }
    }
    return true;
}

在这里插入图片描述

1.3.3 Kruskal算法获取图的最小生成树

这也是接下来要讲的

2. 图的最小生成树问题

对于图的基本知识，请参考博客：Java高阶数据结构 & 图 & 图的表示与遍历_s:103的博客-CSDN博客

下面不作赘述~

2.1 生成树是什么

连通图中的每一棵生成树，都是原图的一个极大无环子图，即：从其中删去任何一条边，生成树 就不在连 通；反之，在其中引入任何一条新边，都会形成一条回路。

若连通图由n个顶点组成，则其生成树必含n个顶点和n-1条边。因此构造最小生成树的准则有五 条：

  1. 只能由图中的边来构造最小生成树
  2. 只能使用恰好n-1条边来连接图中的n个顶点
  3. 选用的n-1条边不能构成回路
    • 当然，都满足第2条，就一定不会构成回路
  4. n-1条边的权和最小
  5. 是连通图
    • 只有连通无向图存在生成树

当然，最小生成树，可能不止一棵

2.2 获取最小生成树算法

贪心算法： 是指在问题求解时，总是做出当前看起来最好的选择。也就是说贪心算法做出的不是整体 最优的 的选择，而是某种意义上的局部最优解。贪心算法不是对所有的问题都能得到整体最优解。

以下两种算法的本质都是贪心算法，虽然数学上不严谨，却能很好的解决这个问题~

  • 不需要纠结，用就是了

2.2.1 Kruskal算法

  • 克鲁斯卡尔算法是全局的贪心算法

步骤：

  1. 选取全局中最短的边，并标记两个顶点
  2. 选取全局中未被标记的边（两个端点都未被标记）
    • 如果几个一样小的，没关系，用哪个都ok
    • 这也是为什么最小生成树可能不唯一的原因
  3. 以此类推…
  4. 在标价前要判断标记后是否成环，如果是，取消此次选择
  5. 直到选出n-1条边，此时计算结束

例子：

  • 求一棵如下图的最小生成树

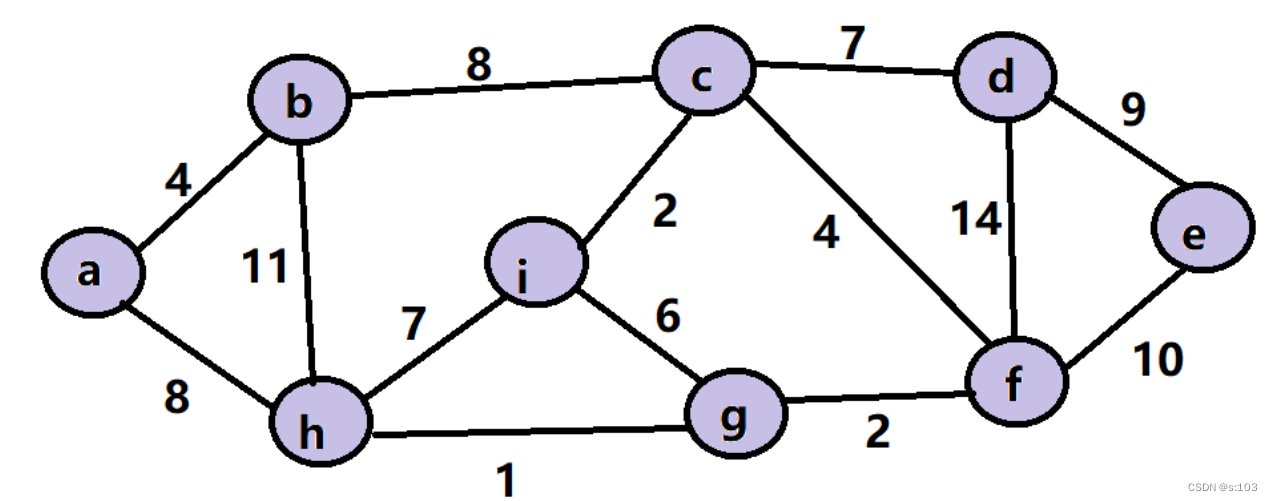
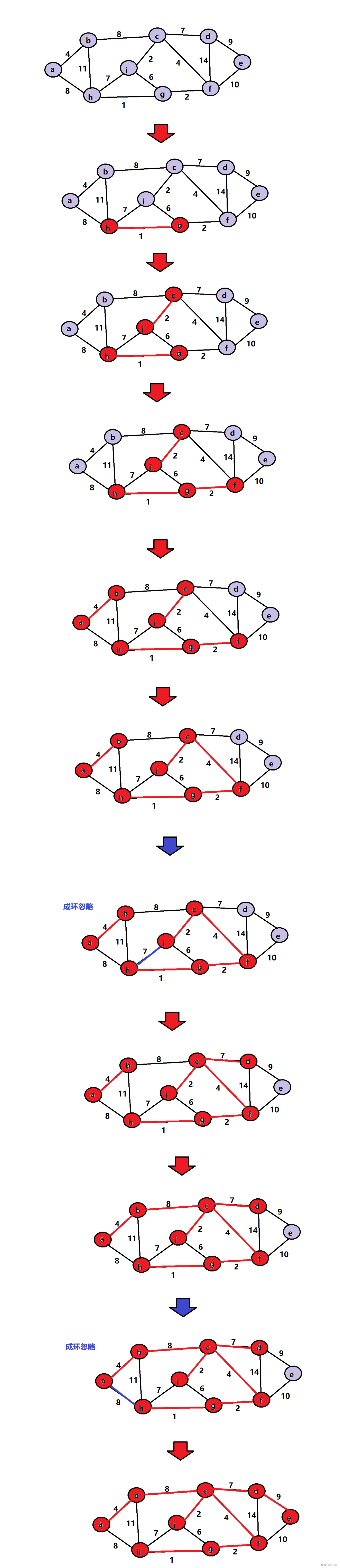
在这里插入图片描述

步骤如下：

在这里插入图片描述

2.2.2 Prime算法

  • 普利姆算法的本质是局部的贪心算法

步骤：

  1. 确定并标记一个起始节点，后续树的生长以此为基础
  2. 生长：在此节点能直接连通的所有节点中，选择一条权最小的边，并标记该节点
  3. 继续生长：在树的所有节点能直接连通的所有节点中，选择一条权最小的边，并标记该节点
    • 不能连通被标记的节点
    • 无向连通图不会出现选不出来的情况
  4. 直到所有节点都被标记则结束，已生长成最小生成树
    • 或者是获得了n-1条边，不成环则一定有n个节点

例子：

  • 求一棵如下图以a的起始节点的最小生成树

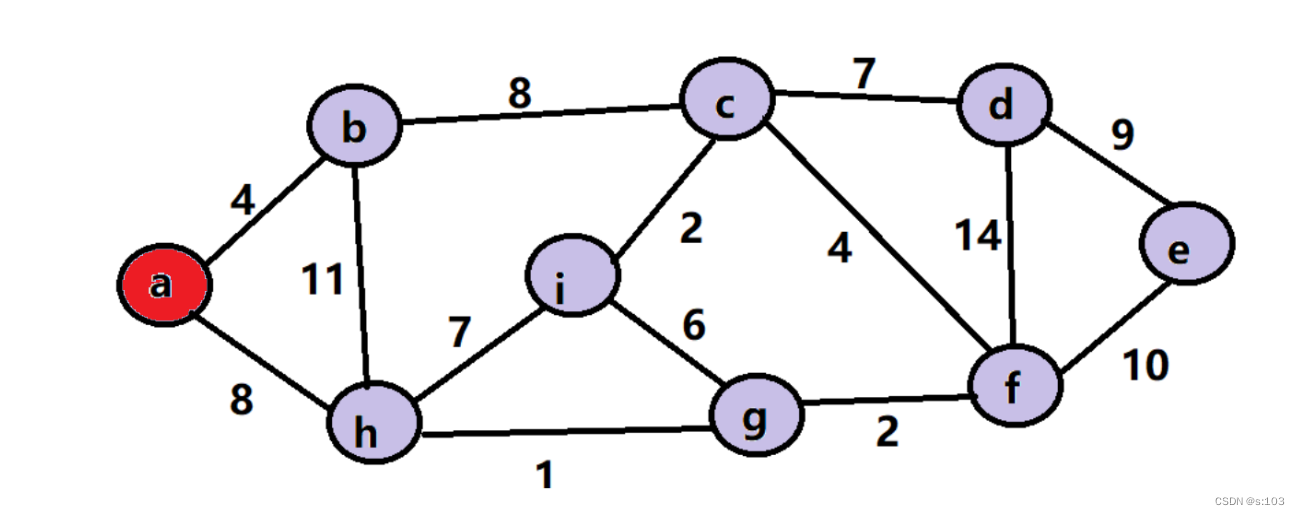
在这里插入图片描述

步骤：

在这里插入图片描述

可见，不同算法求出来的最小生成树不同

2.3 获取最小生成树代码实现

通过刚才的算法讲解，其实思路不难，现在要解决的主要是算法转化为代码~

2.3.1 Kruskal算法代码实现（邻接矩阵）

待处理的问题：

  1. 怎么获得全场最短的边？
  2. 怎么保证不会成环

解决：

  1. 优先级队列 去存储所有的边，每次都取小根堆堆顶，这样可以高效的获取最小边
    • 由于是全局的，所以不存在 “局部最小问题”
  2. 并查集 去整理节点之间的关系，如果一条边的两个节点是有关系（已在同一个图）的，就不能取

代码实现：

  1. Edge类的定义
static class Edge {
    int src;
    int dest;
    int weight;

    public Edge(int src, int dest, int weight) {
        this.src = src;
        this.dest = dest;
        this.weight = weight;
    }
}
  1. 导入并查集这个类（刚才实现的）

在这里插入图片描述

  • 技巧：把代码复制直接粘贴就行了
    • 这样会自动根据public类构建java文件

在这里插入图片描述

  1. 库鲁斯卡尔算法对应方法
/**
 *
 * @param minTree 最小生成树放在图 minTree中
 * @return 最小生成树的权和
 */
public int kruskal(GraphByMatrix minTree) {
    //1. 优先级序列存放所有边
    PriorityQueue<Edge> minHeap = new PriorityQueue<Edge>(
            (o1, o2) -> {
                return o1.weight - o2.weight;
            }
    );
    int n = matrix.length;
    //无向图只需要一条即可
    for (int i = 0; i < n; i++) {
        for (int j = i + 1; j < n; j++) {
            minHeap.offer(new Edge(i, j, matrix[i][j]));
        }
    }
    //最终的权值和
    int retWeight = 0;
    //定义并查集
    UnionFindSet unionFindSet = new UnionFindSet(n);
    int size = 0;//已选边的条数
    //选取n-1条边，如果不成环，必然选中n个节点，
    // 如果队列都空了，都没有n-1条边，则不是无向连通图
    while(size < n - 1 && !minHeap.isEmpty()) {
        Edge minEdge = minHeap.poll();
        int src = minEdge.src;
        int dest = minEdge.dest;
        //如果src与dest师出同门，不能添加
        if(!unionFindSet.isSameSet(src, dest)) {
            System.out.println(arrayV[src] +"--- "
                    +arrayV[dest]+" : "+matrix[src][dest]);
            //这两个节点建立关系
            unionFindSet.union(src, dest);
            //存放在minTree图中，最小生成树返回到这里面
            minTree.addEdge(arrayV[src], arrayV[dest], minEdge.weight);
            //权值和
            retWeight += minEdge.weight;
            //被选中的边的条数加一
            size++;
        }
    }
    return size == n - 1 ? retWeight : Integer.MAX_VALUE;
}

测试：

  • 建立图对象（跟上面的图解一致）
  • 打印最小生成树权和以及最小生成树的邻接矩阵
public static void testGraphMinTree1() {
    String str = "abcdefghi";
    char[] array =str.toCharArray();
    GraphByMatrix g = new GraphByMatrix(str.length(),false);
    g.initArrayV(array);
    g.addEdge('a', 'b', 4);
    g.addEdge('a', 'h', 8);
    //g.addEdge('a', 'h', 9);
    g.addEdge('b', 'c', 8);
    g.addEdge('b', 'h', 11);
    g.addEdge('c', 'i', 2);
    g.addEdge('c', 'f', 4);
    g.addEdge('c', 'd', 7);
    g.addEdge('d', 'f', 14);
    g.addEdge('d', 'e', 9);
    g.addEdge('e', 'f', 10);
    g.addEdge('f', 'g', 2);
    g.addEdge('g', 'h', 1);
    g.addEdge('g', 'i', 6);
    g.addEdge('h', 'i', 7);
    GraphByMatrix kminTree = new GraphByMatrix(str.length(),false);
    kminTree.initArrayV(array);
    System.out.println(g.kruskal(kminTree));
    kminTree.printGraph();
}

public static void main(String[] args) {
    testGraphMinTree1();
}

在这里插入图片描述

2.3.2 Prime算法代码实现（邻接矩阵）

待处理问题：

  1. 怎么找到一条当前标记节点指向未标记节点的边
  2. 这条边怎么保证是最小的

解决：

  1. 由于这种算法明显分为了两种关系：被标记与未被标记

    • 所以直接创建两个集合（HashSet）即可，不需要用到并查集
    • 如果指向的顶点属于被标记过，则不能选择它
    • 选择后目的顶点被标记，也让这条边不会再次被选中

  2. 一样可以用 优先级队列

    • 每次一个顶点被标记的时候，都需要将这个顶点连接的所有边加入队列中

    • 重复的有很多，但是由于刚才的机制，不会出现成环的现象

    • 在这里队列是需要动态更新的，每次都为了找到“局部最小”

代码实现：

  • 普利姆算法对应方法
public int prime(GraphByMatrix minTree, char V) {
    //获取顶点的下标
    int srcIndex = getIndexOfV(V);

    //起始节点集合与目的节点集合
    Set<Integer> srcSet = new HashSet<>();
    Set<Integer> destSet = new HashSet<>();

    //初始化两个集合
    srcSet.add(srcIndex);
    int n = matrix.length;
    for (int i = 0; i < n; i++) {
        if(i != srcIndex) {
            destSet.add(i);
        }
    }

    //从srcSet到destSet集合的边
    //定义优先级队列与初始化优先级队列
    PriorityQueue<Edge> minHeap = new PriorityQueue<>(
            (o1, o2) -> {
                return o1.weight - o2.weight;
                //左大于右为正，为升序小根堆
            }
    );
    for (int i = 0; i < n; i++) {
        if(matrix[srcIndex][i] != Integer.MAX_VALUE) {
            minHeap.offer(new Edge(srcIndex, i, matrix[srcIndex][i]));
        }
    }

    int retWeight = 0;//返回的权值和
    int edgeCount = 0;//已选中的边

    //核心循环
    while(edgeCount < n - 1 && !minHeap.isEmpty()) {
        Edge minEdge = minHeap.poll();
        int src = minEdge.src;
        int dest = minEdge.dest;
        //判断dest是否被标记
        if(!srcSet.contains(dest)) {
            minTree.addEdge(arrayV[src], arrayV[dest], matrix[src][dest]);
            System.out.println(arrayV[src] + "---" + arrayV[dest] + " : "
            + matrix[src][dest]);
            edgeCount++;
            retWeight += matrix[src][dest];
            
            //目的节点被标记：加入srcSet，在destSet除名
            srcSet.add(dest);
            destSet.remove(dest);
            
            //添加新增起始顶点的所有直接连通的边
            for (int i = 0; i < n; i++) {
                //多重保证，安心！
                if(matrix[dest][i] != Integer.MAX_VALUE && destSet.contains(i)) {
                    minHeap.offer(new Edge(dest, i, matrix[dest][i]));
                }
            }
        }
    }
    return edgeCount == n - 1 ? retWeight : Integer.MAX_VALUE;
}

测试：

  • 同上，只是把方法换成prime，并给定起始顶点
public static void testGraphMinTree2() {
    String str = "abcdefghi";
    char[] array =str.toCharArray();
    GraphByMatrix g = new GraphByMatrix(str.length(),false);
    g.initArrayV(array);
    g.addEdge('a', 'b', 4);
    g.addEdge('a', 'h', 8);
    //g.addEdge('a', 'h', 9);
    g.addEdge('b', 'c', 8);
    g.addEdge('b', 'h', 11);
    g.addEdge('c', 'i', 2);
    g.addEdge('c', 'f', 4);
    g.addEdge('c', 'd', 7);
    g.addEdge('d', 'f', 14);
    g.addEdge('d', 'e', 9);
    g.addEdge('e', 'f', 10);
    g.addEdge('f', 'g', 2);
    g.addEdge('g', 'h', 1);
    g.addEdge('g', 'i', 6);
    g.addEdge('h', 'i', 7);
    GraphByMatrix kminTree = new GraphByMatrix(str.length(),false);
    kminTree.initArrayV(array);
    System.out.println(g.prime(kminTree, 'a'));
    kminTree.printGraph();
}

public static void main(String[] args) {
    testGraphMinTree2();
}

在这里插入图片描述

这两个算法的代码可能比较难理解，你可以结合上面的图片和文字讲解去理解代码！

文章到此结束！谢谢观看
可以叫我 小马，我可能写的不好或者有错误，但是一起加油鸭🦆！

后续更新图的最短路径问题和拓扑排序，敬请期待！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/502648.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

1.SpringCloud技术实用02

1.SpringCloud技术实用02

SpringCloud技术实用02 0.学习目标 1.Nacos配置管理 Nacos除了可以做注册中心&#xff0c;同样可以做配置管理来使用。 1.1.统一配置管理 当微服务部署的实例越来越多&#xff0c;达到数十、数百时&#xff0c;逐个修改微服务配置就会让人抓狂&#xff0c;而且很容易出错。…
阅读更多...
ES+Redis+MySQL 高可用架构设计

ES+Redis+MySQL 高可用架构设计

一、背景 二、ES高可用方案 三、会员Redis缓存方案 四、高可用会员主库方案 五、异常会员关系治理 六、展望&#xff1a;更精细化的流控和降级策略 一、背景 会员系统是一种基础系统&#xff0c;跟公司所有业务线的下单主流程密切相关。如果会员系统出故障&#xff0c;会…
阅读更多...
网络安全信息收集初探之域名信息收集

网络安全信息收集初探之域名信息收集

网络安全信息收集初探之域名信息收集 域名信息收集工具oneforall收集子域名扫描单个域名批量扫描域名oneforall 额外参数 google hacking 证书收集子域名证书子域名在线收集网站子域名收集的各种细节 域名信息收集工具 oneforall收集子域名 扫描单个域名 python oneforall.p…
阅读更多...
进阶自动化测试，这3点你一定要知道的...

进阶自动化测试，这3点你一定要知道的...

自动化测试指软件测试的自动化&#xff0c;在预设状态下运行应用程序或系统&#xff0c;预设条件包括正常和异常&#xff0c;最后评估运行结果。将人为驱动的测试行为转化为机器执行的过程。 自动化测试框架一般可以分为两个层次&#xff0c;上层是管理整个自动化测试的开发&a…
阅读更多...
云渲染农场具有什么特点？

云渲染农场具有什么特点？

众所周知&#xff0c;渲染农场的出现是为了解决长时间的图像渲染问题。渲染农场的底层搭建原理是利用很多计算机、网络和操作系统来构建一个庞大的计算群组&#xff0c;把一个渲染任务从一台机器分发到这个计算群组&#xff0c;从而达到短时间内能够快速得到渲染结果。 到了20…
阅读更多...
分布式搜索引擎es 面试突击

分布式搜索引擎es 面试突击

es elastocsearch 倒排索引是在数据查询之前建立&#xff0c;在查询的时候可以直接通过关键词定位到文档内容。用空间换时间 分布式架构原理说一下&#xff1f; es底层是基于lucene来的 大概就是一个用于全文检索的jar包 用es来做分布式的搜索引擎 可以承载一秒钟几千的…
阅读更多...
【Vue工程】005-Vue Router

【Vue工程】005-Vue Router

【Vue工程】005-Vue Router 文章目录 【Vue工程】005-Vue Router一、概述1、Slogan2、官网3、参考文章 二、安装三、基本使用1、定义路由2、创建路由实例3、在 main.ts 注册路由4、在 App.vue 定义路由出口 四、嵌套路由1、修改路由2、定义嵌套路由出口 五、配置404页面六、声明…
阅读更多...
联合索引该如何选择合适的列？

联合索引该如何选择合适的列？

前面一篇文章&#xff0c;松哥和大家聊了 MySQL 中的索引合并&#xff0c;虽然 MySQL 提供了索引合并机制来提升 SQL 执行的效率&#xff0c;然而在具体实践中&#xff0c;如果能避免发生索引合并是最好的&#xff0c;毕竟这是没办法的办法&#xff0c;是一个下下策。发生索引合…
阅读更多...
Wikidata 模型分析+实体抽取+数据处理

Wikidata 模型分析+实体抽取+数据处理

Wikidata 数据分析与处理 需求&#xff1a;Wikidata 数据描述了很多实体&#xff0c;以及实体属性。比如某一个公司/组织/机构名称是&#xff1a;阿里巴巴&#xff0c;对数据内该组织的相关属性进行观察、分析、治理、抽取等&#xff0c;最后用图数据库进行存储和展示其关系&am…
阅读更多...
为什么半导体FAB生产线需要EAP系统？

为什么半导体FAB生产线需要EAP系统？

在半导体制造中&#xff0c;设备自动化系统EAP&#xff08;Equipment Automation Program&#xff09;是不可或缺的重要软件&#xff0c;它是连接MES、RMS、APC、FDC等上层系统和设备层的桥梁&#xff0c;用于管控生产线上的所有机台&#xff0c;并实现设备运行的自动化。 作为…
阅读更多...
QT+OpenGL高级数据和高级GLSL

QT+OpenGL高级数据和高级GLSL

QTOpenGL高级数据和高级GLSL 本篇完整工程见gitee:QtOpenGL 对应点的tag&#xff0c;由turbolove提供技术支持&#xff0c;您可以关注博主或者私信博主 高级数据 OpenGL中的缓冲区 对象管理特定的GPU内存 在将缓冲区绑定到特定的缓冲区目标时候赋予它意义 OpenGL在内部会保…
阅读更多...
项目环境配置、不知晓问题自己搜索后得到的解答

项目环境配置、不知晓问题自己搜索后得到的解答

目录 Anolis OS龙蜥操作系统 Kernel Selection 4.18.0(RHCK) Compatible with RHEL (kernel-4.18.0) 4.19.91(ANCK) Support Anolis OS verified platform (kernel-4.19.91) 这两个内核选择哪个比较好呢&#xff1f; 我的C盘有些满&#xff0c;我该如何删除一些我需要的东西…
阅读更多...
docker网络访问和端口映射

docker网络访问和端口映射

docker网络访问和端口映射 文章目录 docker网络访问和端口映射1.docker容器网络1.1.创建一个centos7的容器1.2.docker网络原理图 2.端口映射2.1.创建一个新的IP2.2.多个IP端口映射2.3.随机端口命令 1.docker容器网络 指定映射&#xff08;docker 会 自动添加一条iptables规则来…
阅读更多...
wisp5.0 学习日记2

wisp5.0 学习日记2

学习日记 昨天的报错尝试1&#xff0c;在CCS中设置USB FET尝试2 csdn解决方案1尝试3 查看仿真器的驱动是否安装成功 昨天的报错 MSP430: Error initializing emulator: No USB FET was found 尝试1&#xff0c;在CCS中设置USB FET 打开CCS&#xff0c;选择“Window” -> …
阅读更多...
在线文档编辑工具哪个更好？

在线文档编辑工具哪个更好？

在线文档编辑工具相当于一个轻量级、跨平台、多途径的Office。使用在线文档编辑工具&#xff0c;首先我们不用安装Office软件&#xff1b;其次在电脑网页上、手机小程序里我们都可以使用在线文档进行简单的编辑&#xff1b;最后我们编辑的文档可以实时更新、分享、协作等。今天…
阅读更多...
供应商标准化管理难？云时通助力国药器械成功打造医疗器械行业SRM管理平台！

供应商标准化管理难？云时通助力国药器械成功打造医疗器械行业SRM管理平台！

中国医疗器械有限公司(CMDC,简称“国药器械”)&#xff0c;始建于1966年&#xff0c;隶属于国药集团&#xff0c;是其医疗器械板块的主力军。国药器械有分子公司300家左右&#xff0c;年销售额300多亿&#xff0c;国内最大的医疗器械商业流通企业&#xff0c;产品覆盖医疗器械所…
阅读更多...
软件测试简历？面试题？企业面试官想要什么？我不再和offer失之交臂...

软件测试简历？面试题？企业面试官想要什么？我不再和offer失之交臂...

目录&#xff1a;导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结&#xff08;尾部小惊喜&#xff09; 前言 软件测试面试题简历…
阅读更多...
vivado跨时钟域路径分析

vivado跨时钟域路径分析

若要查看跨时钟域路径分析报告&#xff0c;可选择以下内容之一来查看&#xff1a; A, Reports > Timing > Report Clock Interaction B, Flow Navigator > Synthesis > Report Clock Interaction C, Flow Navigator > Implementation > Report Clock Inte…
阅读更多...
【网络安全】--win提权

【网络安全】--win提权

win提权 提权目的提权常用命令提权实战常见的payload利用1. 安装虚拟机win2008和kali2. 创建普通用户3. 切换用户4. kali生成木马并发送到被攻击服务器上5. 被攻击方运行生成的木马文件7. 查看可利用漏洞8. 尝试利用exp提权 at/sc/ps命令提权at命令提权sc命令提权ps命令提权 提…
阅读更多...
换个花样玩C++（8）吃不透内存布局，坑的是自己，万字经验告诉你类的内存布局

换个花样玩C++（8）吃不透内存布局，坑的是自己，万字经验告诉你类的内存布局

C++内存布局是老生常谈的话题，无论是笔试面试，都会涉及到该类问题，那么这一章节，我们就聊聊内存布局到底是怎么布局的，聊完之后我保证你仍然会回味无穷，并且我提供的几个例子也会让你再一步步踩入雷区。 C++程序的内存布局 C++的内存布局区域我们大体上分为四个：全局数据…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023