TCP CUBIC 应该是迄今为止综合表现最优秀的算法,其中有两个亮点,一个是 RTT 无关性,另一个是可扩展性。RTT 无关性表现在 CUBIC 的 cwnd 表达式中没有 RTT 因子,而可扩展性则来自于曲线本身:
- 随着 BDP 增加,CUBIC 三次曲线拐点(从上凸到下凸)逐渐右上移,cwnd 初始增量更大,初始 AI 效率更高。
- 无论 BDP 多大,CUBIC 三次曲线都保证在接近饱和时 cwnd 缓慢逼近 Wmax,降低丢包损失。
- 无论 BDP 多大,越过 Wmax 后(已经够本了),CUBIC 加速 probe,高效率获取 extra 容量。
而所有这一切,CUBIC 仅需要绝对时间轴上的 ACK 驱动。
TCP CUBIC 曲线只有一条:
W c u b i c ( t ) = C ∗ [ t − ( K = β ∗ W m a x C 3 ) ] 3 + W m a x W_{cubic}(t) = C*[t-(K=\sqrt[3]{\dfrac{\beta *W_{max}}{C}})]^3 + W_{max} Wcubic(t)=C∗[t−(K=3Cβ∗Wmax)]3+Wmax
其中 C = 0.4,beta = 0.2(2 个参数可调),C 决定曲线形状,Wmax 和 K 只影响曲线的位置。显而易见,BDP 越大,Wmax 越大,同一坐标系中,曲线拐点越靠右上:
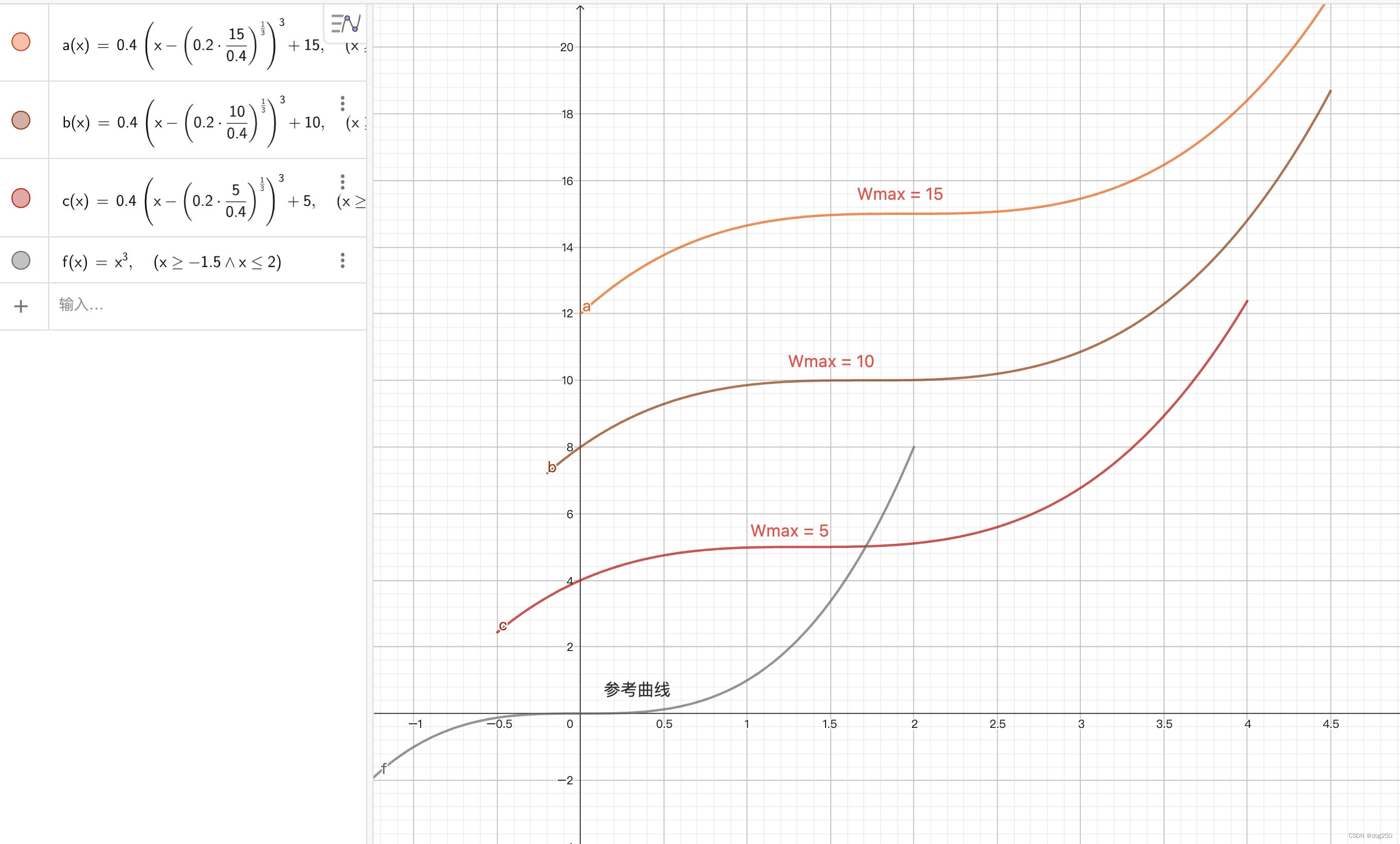
若以每个 AIMD 周期做参照,只取曲线 x >= 0 的部分,即可看出周期开始时,BDP 越大,Wmax 越大,曲线的增长越快,反之在小 BDP 场景,曲线离原点太近,增长过于缓慢。
这就是 CUBIC 之 TCP Friendly region 要解决的问题。
在 CUBIC 曲线旁边同时画出 Reno(or TCP Tahoe,or Standard TCP) 曲线:
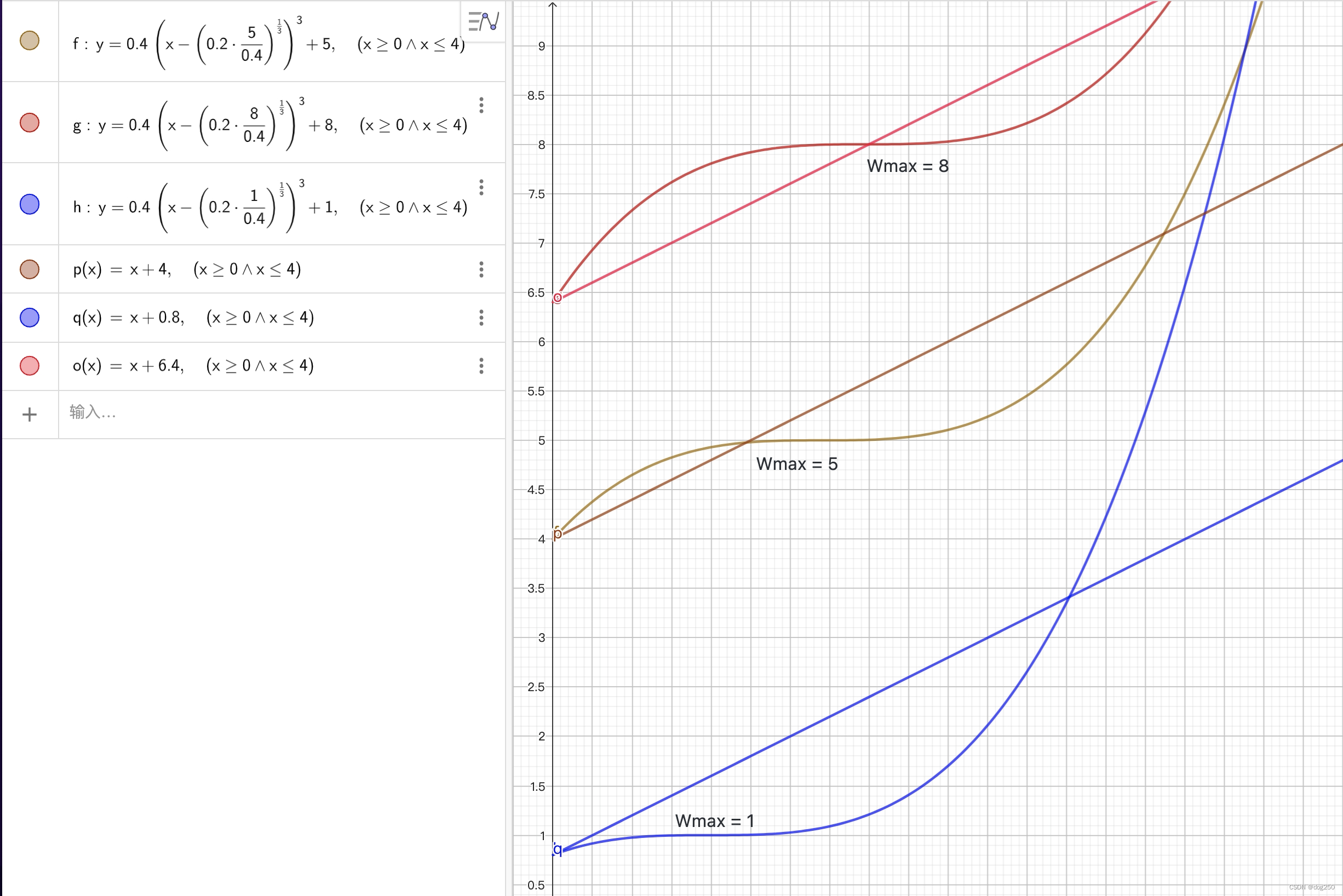
可见 Wmax 越大,CUBIC 初始优势越大,这就是 CUBIC 可扩展性,但另一方面,当 BDP 小到一定程度,总会存在一个点,Reno 曲线即使在开始时也位于 CUBIC 曲线上方,此时 Reno 效率高于 CUBIC,在这种情况下,CUBIC 选择使用 Reno 的结果。
这就是 CUBIC RFC8312 Principle 2:
CUBIC promotes per-flow fairness to Standard TCP. Note that Standard TCP performs well under short RTT and small bandwidth (or small BDP) networks. There is only a scalability problem in networks with long RTTs and large bandwidth (or large BDP). An alternative congestion control algorithm to Standard TCP designed to be friendly to Standard TCP on a per-flow basis must operate to increase its congestion window less aggressively in small BDP networks than in large BDP networks. The aggressiveness of CUBIC mainly depends on the maximum window size before a window reduction, which is smaller in small BDP networks than in large BDP networks. Thus, CUBIC increases its congestion window less aggressively in small BDP networks than in large BDP networks. Furthermore, in cases when the cubic function of CUBIC increases its congestion window less aggressively than Standard TCP, CUBIC simply follows the window size of Standard TCP to ensure that CUBIC achieves at least the same throughput as Standard TCP in small BDP networks. We call this region where CUBIC behaves like Standard TCP, the “TCP-friendly region”.
注意,这里的 friendly 不是 CUBIC 对 Reno 的退让,恰恰相反,CUBIC 的可扩展性在小 BDP 场景损害了效率,而这种场景下 Reno 的效率更高。
这不能说是 CUBIC 的代价,而是事实证明 Reno 的 AIMD 已足够收敛,这是拥塞控制的根本目标,而 CUBIC 的 cwnd 如果不如 Reno 的大,同样满足收敛性的前提下,选择效率更高的。
算法很简单:CUBIC 算出来的 cwnd 如果比 Reno 还要小,就选择 Reno 的结果。
接下来看 CUBIC 的拐点控制。
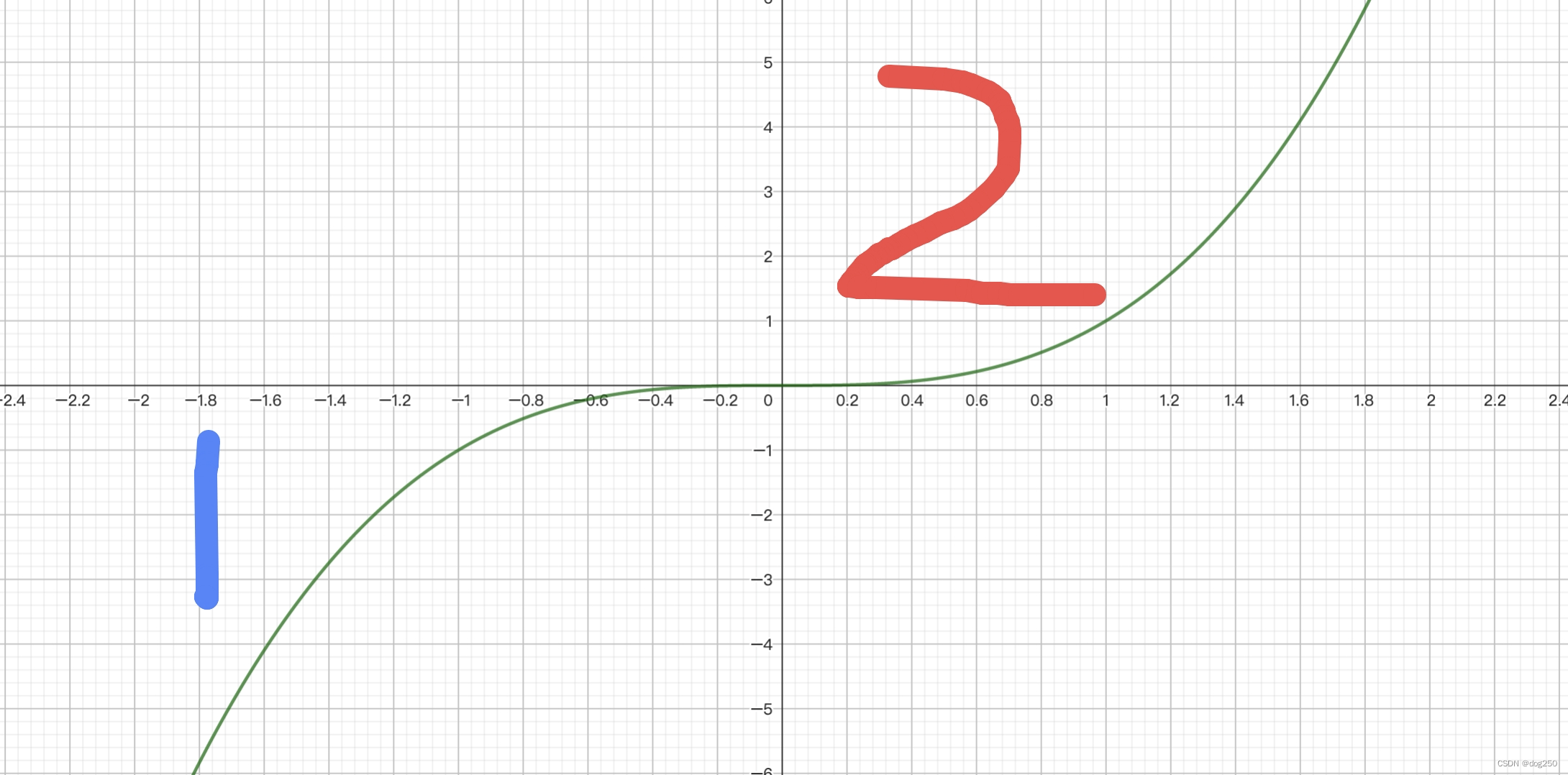
CUBIC 可以作为一种 “基于拐点” 的算法来理解,这个拐点就是其高效的原因。无论如何,先快后慢地逼近网络饱和容量是正确的,反之如果开始慢,网络利用率低,如果后面快,则更容易丢包。这就是 CUBIC 的上凸区域,下图的面积 1 越小越好。
再看 probe 区域,面积 2 如果太大,虽长期不丢包,但探测不够快,长 RTT 时带宽利用率下降,如果足够小,可在更短时间内 probe 到新 Wmax,降低下一个周期的面积 1,显然下凸曲线可以满足让面积 2 足够小但又不至于过分小,这就是 CUBIC 拐点自适应:
CUBIC 的问题在于它无法在长肥管道场景保持稳定。
首先,网络流量并非持续稳定,由于 RTT 过长,夜长梦多,就像导航经常误判那样,从上海出发去温州显示畅通,等到达台州时可能就会拥堵,因此 Wmax 不一定可保持,而 CUBIC 本身必须对 loss 进行 MD 反应以保证收敛,而 Wmax 的不稳定性将导致对丢包的频繁反应。
其次是一个实现问题,它来自于上述大 RTT 导致的波动影响力(本质还是夜长梦多),CUBIC 以 minRTT 作为一个计算周期:
if dMin then dMin ← min(dMin, RTT)
else dMin ← RTT
t ← tcp_time_stamp + dMin − epoch start
target ← origin_point + C(t − K)^3
如果 RTT 太长,将导致估算误差过大,曲线呈现阶梯状不再平滑,很容易 “越过” 拐点误入 probe 区域,这将导致拐点估算误差。虽然 CUBIC 用绝对时间采样打点描绘曲线,消除了 RTT 依赖,解决了 RTT 不公平问题,但 RTT 却依然影响着曲线平滑程度,RTT 越小曲线越光滑,越 “CUBIC"(形容词),然而问题是 RTT 越小,越倾向于受 TCP Friendliness 控制而采用 Reno。
这是个有趣的矛盾,RTT 越大,CUBIC 优势越大,但计算周期也越久,结果越不精确,反之 RTT 越小,CUBIC 效率越低,越倾向于 Reno。有个思路是压缩计算周期,但这本质上还是 ACK 时钟的问题。
BBR 为应对 Delayed ACK,聚合 ACK 也采取了一些 “优化”,并打入一些 patch,同样没从根本上解决问题,对 CUBIC 也一样,虽然压缩计算周期很容易,比如将 RTT/4 作为输入,但如果 RTT/4 后没有 ACK 到达,就会进入空窗期,在 ACK 聚合场景,ACK 本就稀疏到达,问题更加明显,最终的方案似乎只有抛弃 ACK 时钟而采用本地时钟,但这很容易违背数据包守恒原则而引发拥塞。
CUBIC 算法非常优秀,仅输入极少的信息便获得可扩展性和自适应性(另一些算法,比如 tcp scalable 就没有这等效果),但实现和部署场景可能会严重影响 CUBIC 实际效果,比如对丢包的过度反应,比如长 RTT 计算精度问题,但不可否认这些问题都是可以解决的,其大部分的错存在的 Linux kernel 对拥塞状态机的实现本身,是 Linux kernel 绕不开的拥塞状态机限制了 CUBIC(Linux 4.9 引入 BBR 后已经解放了这个状态机依赖,但 CUBIC 大概率不会重新实现)。
回到 CUBIC 本身,它虽被列为 Loss-based cc,但不意味着它依赖深 buffer 而故意引入大时延,BDP 本就很大的场景,小 buffer 非常适合 CUBIC,且只需要有一跳小 buffer 即可。
和 BBR 不同的只是 CUBIC 不会主动腾挪对 buffer 的占用,但如果给 CUBIC 配置一个小 buffer 路径,它依然可以高效填充有效带宽本身而不是 buffer。
影响时延的不是算法,而是 buffer 本身。然而,这种论点有悖于设备商做宣传的动机而容易被误认为缺斤短两,再说了,存储成本越来越低,反过来导致延时成本越来越低。这又是时间和空间的本质矛盾体现,但却不给人选择权,buffer 就摆在那里,用不用不由你,关键看你怎么用。
CUBIC 绝对是一个非常优秀的 cc,它作为 Linux 以及很多其它系统缺省 cc 不是没有理由,CUBIC 在各方面的表现都很优秀,但受制于 Linux kernel 的 cc 框架,在实现上并非那么完备。若不是 BBR 出现,人们普遍都基于 CUBIC 做优化,为其添加 pacing 支持,缓和过度的丢包反应,为其增加时延测量…况且 BBR 由于太新被无限放大了优势而忽略了缺点, 造成了过度吹捧,三天两头有 BBR-based 优化版 BBR 的 paper 放出却还是老套而无突破,卷风不亚于 Linux kernel 社区。有必要科普一下 CUBIC beyond BBR,作此文。
浙江温州皮鞋湿,下雨进水不会胖。