小朋友们好,大朋友们好!
我是猫妹,一名爱上Python编程的小学生。
欢迎和猫妹一起,趣味学Python。
今日主题
你知道我国历史上有个王朝叫北魏吗?
北魏(386年—534年),南北朝时期北朝的第一王朝。
也称“后魏”“拓跋魏”“元魏”,鲜卑族拓跋氏所建,传12帝(列入正史帝纪者)
你知道北魏王朝有个著名的数学家叫张丘建吗?
他从小聪明好学,酷爱算术。
一生从事数学研究,造诣很深。
“百鸡问题”是中古时期,关于不定方程正整数解的典型问题,邱建对此有精湛和独到的见解。
著有《张邱建算经》3卷。后世学者北周甄鸾、唐李淳风相继为该书作了注释。刘孝孙为算经撰了细草。
算经的体例为问答式,条理精密,文词古雅,是中国古代数学史上的杰作,也是世界数学资料库中的一份遗产。
你知道张丘建的代表作《算经》吗?
你知道《算经》中有个著名的数学问题叫百鸡百钱吗?
鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一。百钱买百鸡,问鸡翁、鸡母、鸡雏各几何?
公鸡5文钱一只,母鸡3文钱一只,小鸡3只一文钱。用100文钱,买100只鸡。问公鸡、母鸡、小鸡各多少只?
方程解法
如果上了初中,应该会学到方程,这个问题可以用方法来求解。
未知数称为元,未知数的幂称为次。
假设公鸡、母鸡、小鸡分别为x、y、z只。
由题可得以下方程:
① x+y+z=100 (鸡的总数量为100只)
② 5x+3y+1/3z=100 (鸡的总价格为100文)
根据以上方程,可以得到以下解:
7x+4y=100
本质上是二元一次方程的整数解问题。
x大于等于0,小于等于20
y大于等于0,小于等于33
x=(100-4y)/7
y=(100-7x)/4
化简得x<=14 y<=25,然后x依次0~14逐一取值计算进行验证判断即可。

二元一次方程的整数解属于初中数学问题:
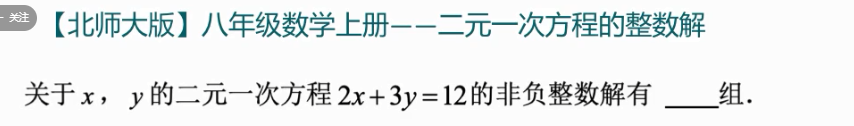
答案是3组
Python遍历解法
在Python编程中,通过穷举法的方式找出所有解法。
-
枚举公鸡的数量x=0~20,步长为1。
-
在枚举公鸡数量x的前提下,枚举母鸡的数量y=0~33,步长为1。
-
根据x和y的值,计算出小鸡的数量z=100-x-y。
-
判断当前三种鸡的数量是否符合条件,即5x+3y+z/3=100,如果符合,则输出当前解法。
for x in range(0, 21):for y in range(0, 34):z = 100 - x - yif 5*x + 3*y + z/3 == 100:print("公鸡:%d只,母鸡:%d只,小鸡:%d只" % (x, y, z))
公鸡:0只,母鸡:25只,小鸡:75只公鸡:4只,母鸡:18只,小鸡:78只公鸡:8只,母鸡:11只,小鸡:81只公鸡:12只,母鸡:4只,小鸡:84只
程序用了两层循环,其实还可以用一层循环,此时理解起来稍微麻烦些,但是运行效率会更高效一些。
for x in range(0, 21):y = 25 - 7*x/4z = 75 + 3*x/4if x%4==0 and y >=0:print("公鸡:%d只,母鸡:%d只,小鸡:%d只" % (x, y, z))
公鸡:0只,母鸡:25只,小鸡:75只公鸡:4只,母鸡:18只,小鸡:78只公鸡:8只,母鸡:11只,小鸡:81只公鸡:12只,母鸡:4只,小鸡:84只
穷举法
所谓穷举法,从可能得解的集合中一一枚举各元素,用题目给定的检验条件判定哪些是无用的,哪些是有用的。
由于穷举法需要遍历所有元素,因此它的时间性能往往是最低的,指数级的时间开销往往都是采用穷举带来的,但是它依旧是很重要的算法设计思想。理论上,穷举法可以解决许多计算领域的问题(只要机器性能足够或者时间开销可承受)。

百钱买百鸡问题是一道经典的数学问题,通过方程解法和编程解法,可以找出所有符合条件的解法。
方程解法适用于小规模的问题,对于大规模的问题,可以使用编程解法进行计算。
编程解法使用穷举的方式,可以找出所有解法,但计算量较大,需要耗费一定时间和计算资源。
对于现在的计算机来说,这都不是事儿!

好了,我们今天就学到这里吧!
如果遇到什么问题,咱们多多交流,共同解决。
我是猫妹,咱们下次见!