1.信息的表示和处理

news2025/1/15 16:52:52

基础

进制转换

10-2

字数据大小

在这里插入图片描述

寻址和字节顺序（大小端）

在这里插入图片描述
01 23 45 67
大端法：最高有效字节（01）在最前面（相当于正序）
小端法：最低有效字节（67）在最前面（相当于不彻底倒序）

移位

逻辑右移：左侧补k个0
算术右移：左侧补k个符号位

异或^

系统习题10：swap

void inplace_swap(int *x,int *y){
	*y = *x ^ *y;
	*x = *x ^ *y;
	*y = *x ^ *y;
}

每个元素是自己的逆元，x ^ x = 0

整数

整数表示

原码00

最高有效位是符号位
[+0]_原=0,0000
[-0]_原=1,0000
-1无法表示

补码

在这里插入图片描述
补码范围形如：[-128,127]
按位取反，末位加1
[+0.0000]_补=[-0.0000]_补=0.00000
由y_补求(-y)_补：连同符号位，按位取反，末位加1
现代机器使用补码较多，主存地址通常用无符号数表示

反码00

最高有效位的权重是-7
按位取反
[+0]_反=0,0000
[-0]_反=1,1111

移码

与补码仅符号位不同

类型转换

只是改变解释方式
注意min、0、-1等特殊值

整数运算

非

无符号数的非，0的逆元是0
补码的非，T_min的非是T_min

加法

无符号数加法的溢出判断
s<x或s<y
补码加法的溢出判断
(1)单符号位
正溢出：x>0并且y>0，但s<=0
负溢出：x<0并且y<0，但s>=0

(2)C_s是符号位进位，C₁是最高数位进位

(3)双符号位
补码求反
-x和~x+1结果相同（逐位取反再加1）

零标志ZF，都有意义
溢出标志OF：有符号整数运算时溢出
符号标志SF：结果的符号，对无符号数无意义
进/借位标志CF：无符号整数的进位/借位

乘法

T**和U*的位级等价性

在这里插入图片描述
截断后，无符号数的乘积=补码的乘积

booth(补码比较法)：

其中，Y_n和Y_n+1是乘数的后两位
在这里插入图片描述

除法

整数除法总是向0舍入
U/：向0舍入
T/：
若不加偏量，算术右移，向下舍入
加偏量 ((1<<k)-1)，算术右移，向0舍入

在这里插入图片描述

浮点数

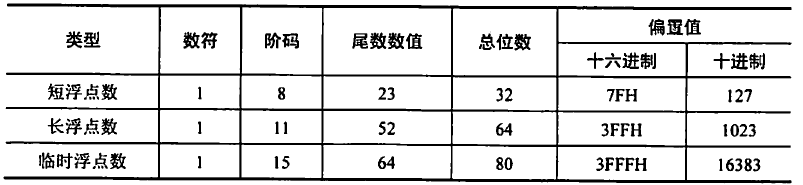
IEEE754标准

在这里插入图片描述
N=(-1)^s X M X R^E
数符S
尾数M：原码小数表示，范围是(1,2-a)或(0,1-a)
阶码E：用移码表示
基数R：2、4、16等

系统习题6：int->float

3510593.0的float
（3510593）₂ = 0011 0101 1001 0001 0100 0001 = 1.1 0101 1001 0001 0100 0001X10²¹
float的小数为23位，需要补2个0，省略小数点前面的1
小数部分：1 0101 1001 0001 0100 0001 00
阶码：21+bias=21+127=148=（1001 0100）₂
完整float：0 1001 0100 1 0101 1001 0001 0100 0001 00
符号1 + 阶码8 + 小数23=float32位
3510593的int与 3510593.0的float 有21位重合（平移2位后重合）

规格化

在这里插入图片描述
规格化的值
阶码E=e-bias
对于float，e的范围(1，2⁸-1-1=254)，bias=2^8-1-1=127，所以E的范围(-126，127)
尾数M=1+f，隐含的以1开头

非规格化的值
阶码E=1-bias
尾数M=f，没有隐含的开头的1
从非规格化值平滑转换到规格化值
表示那些非常接近0.0的数，逐渐溢出，可能的数值分布均匀地接近于0.0

对于4位阶码，3位尾数的浮点格式，bias=7
正负0
最小非规格化正数E=1-bias=-6，尾数M=f=001=1/8，值为2^-6X2^-3
最大非规格化正数E=1-bias=-6，尾数M=f=111=7/8，值为2^-6X(1-2^-3)
最小规格化正数E=0001-bias=-6，尾数M=1+f=1，值为2^-6X1
最大规格化正数E=1110-bias=7，尾数M=1+f=15/8，值为2⁷X(2-2^-3)

规格化：
基数为2时，1/2<=|尾数|<1，即最高位为1

向偶数舍入：只对于中间值
在这里插入图片描述