一、不要二
题目:
牛客网链接:不要二_牛客题霸_牛客网
描述
二货小易有一个W*H的网格盒子,网格的行编号为0~W-1,网格的列编号为0~H-1。每个格子至多可以放一块蛋糕,任意两块蛋糕的欧几里得距离不能等于2。
对于两个格子坐标(x1,y1),(x2,y2)的欧几里得距离为:( (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2) ) 的算术平方根。
小易想知道最多可以放多少块蛋糕在网格盒子里。输入描述:
每组数组包含网格长宽W,H,用空格分割.(1 ≤ W、H ≤ 1000)
输出描述:
输出一个最多可以放的蛋糕数
示例1
输入:3 2
输出:4
解析:
本题的关键在于解析任意两块蛋糕的欧几里得距离不能等于2。
因为想知道存在多少块蛋糕在网格盒子里,我们可以利用条件将不满足要求的排除掉,剩余的就是可以放入盒子里的。
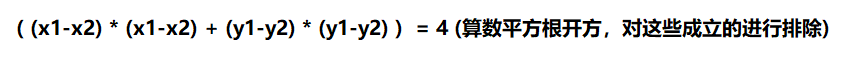
根据条件,因为x1x2y1y2均为网格盒子对应二维数组的下标,为整数,所以就有下面的数字举例:
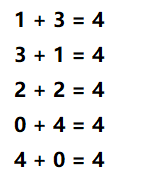
但是+两边均是相同的数字相乘,排除后只剩下:

所以,我们可以推导出如下的限制条件:
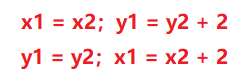
我们的整体思路如下:根据输入的wh构建w*h的二维数组,首先全部初始化为1.然后每次根据i, j + 2 i + 2, j 去对应下标置为0(注意越界),统计1的个数即可。
解答:
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int w, h, count = 0;
cin >> w >> h;
vector<vector<int>> vv;
vv.resize(w); // 初始化行
for(auto & v : vv) v.resize(h, 1); // 初始化列
for(int i = 0; i < w; ++i)
{
for (int j = 0; j < h; ++j)
{
if (vv[i][j] == 1)
{
++count;
// 根据欧几里得距离不等于2进行置零
if (i + 2 < w) vv[i + 2][j] = 0;
if (j + 2 < h) vv[i][j + 2] = 0;
}
}
}
cout << count << endl;
return 0;
}二、把字符串转换为整数
题目:
牛客网链接:把字符串转换成整数_牛客题霸_牛客网
描述
将一个字符串转换成一个整数,要求不能使用字符串转换整数的库函数。 数值为 0 或者字符串不是一个合法的数值则返回 0
数据范围:字符串长度满足0≤n≤100
进阶:空间复杂度O(1) ,时间复杂度O(n)注意:
①字符串中可能出现任意符号,出现除 +/- 以外符号时直接输出 0
②字符串中可能出现 +/- 且仅可能出现在字符串首位。
输入描述:
输入一个字符串,包括数字字母符号,可以为空
返回值描述:
如果是合法的数值表达则返回该数字,否则返回0
示例1
输入:"+2147483647"
返回值:2147483647
示例2
输入:"1a33"
返回值:0
解析:
字符串转整型,我们首先明确单个数字字符如何转为整数?可以利用ASCII码值进行转换,即每个数字字符-'0'就可以得到了。
那么一个字符串从高位向低位(从左到右),我们就可以利用每次转换下来得数字加上先前计算出的数字*10。(递进关系)
本题需要注意的是存在非数字字符和首字符可以是'+'、'-'的问题。首先在上面递进的时候我们自然需要判断是否非数字字符,是的话可以直接返回0,但是当首字符判断是+或者-任意一种,应该跳过首字符。
解答:
class Solution {
public:
int StrToInt(string str) {
if (str.empty()) return 0;
int res = 0, sum = 0;
int flag = 1;
if (str[0] == '-')
{
flag = -1;
res++;
}
else if (str[0] == '+') res++;
for (;res < str.size(); ++res)
{
// 首先判断是否为非数字
if (str[res] < '0' || str[res] > '9') return 0;
sum = sum * 10 + str[res] - '0';
}
return sum * flag;
}
};