在一般的距离保护II段和III段的整定计算中，分支系数的计算是必须要的，本文选自电力系统继电保护（第二版）（张保会老师主编）P94-P97页的例题，分析其中分支系数的计算公式。
我们在前面的章节中知道了助增和外汲的公式，定性的知道了两种情况对于实际整定的影响。但是这道题既有助增，又有外汲，不太好理解公式的含义，我在这里给出的是一种方便理解的办法。
首先给出例题中的图：

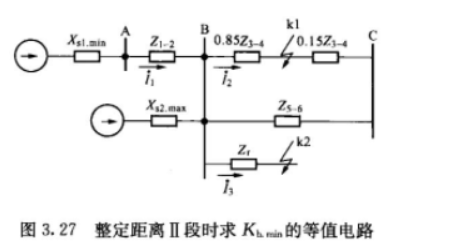
首先假定BC段的最长保护范围是85%（考虑到其距离一段不可能保护线路全长），也就是把BC整段的阻抗分为85%和15%。
然后例题的解答里直接给出了Kb的表达式，让我非常懵，我把这个公式写在下面：
$$K_b=\frac{I_2}{I_1}=\frac{X_{s1}+X_{1-2}+X_{s2}}{X_{s2}}\times \frac{\text{（}1+0.15\text{）}{Z}_{3-4}}{2Z_{3-4}}=\text{（}\frac{X_{s1}+Z_{1-2}}{X_{s2}}+1\text{）}\times \frac{1.15}{2}$$
很明显这里是跳步了，我把跳的步补上，同时把B母线写成B1和B2，如下图所示即为推导过程（很明显B1、B2是一个点，分开写是为了好理解）：

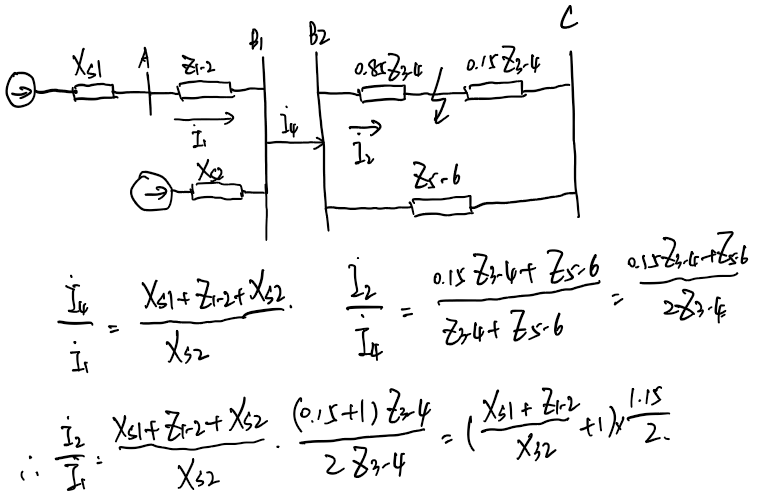
如果考试时候还是建议大家写一个中间步骤，不然上下颠倒步骤一多很容易出错