704.二分查找
解析:
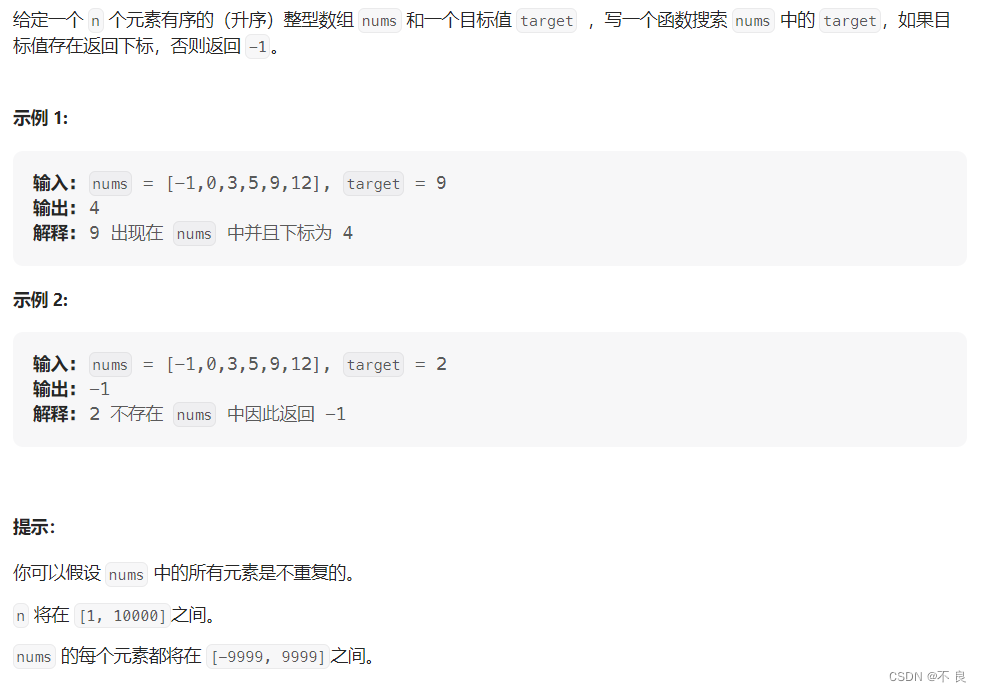
思路一:暴力解法,直接遍历,从头开始查找,如果找到直接返回下标,找不到返回-1。
class Solution {
public:
int search(vector<int>& nums, int target) {
for(int i = 0; i < nums.size(); i++)
{
if(nums[i] == target)
return i;
}
return -1;
}
};
思路二:二分查找;
使用二分查找的前提条件是:
1.数组为有序数组;
2.数组中无重复元素(一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的)。
二分查找中,最容易搞混的两点为:
1.
while循环里面的条件应该是while(left < right)还是while(left <= right);2.
right再次赋值的时候应该是right = middle还是right = middle - 1。二分查找分析:
首先我们要对区间的定义进行明确,即确定这个区间是左闭右闭(
[left,right],区间包含left和right)还是左闭右开([left,right),区间包含left,但是不包含right),一般情况下都是这两种情况;然后针对不同区间的定义,进行边界条件的处理(即while循环条件)。对于区间的定义不一样,是直接影响边界条件的处理的(即
while循环条件)。
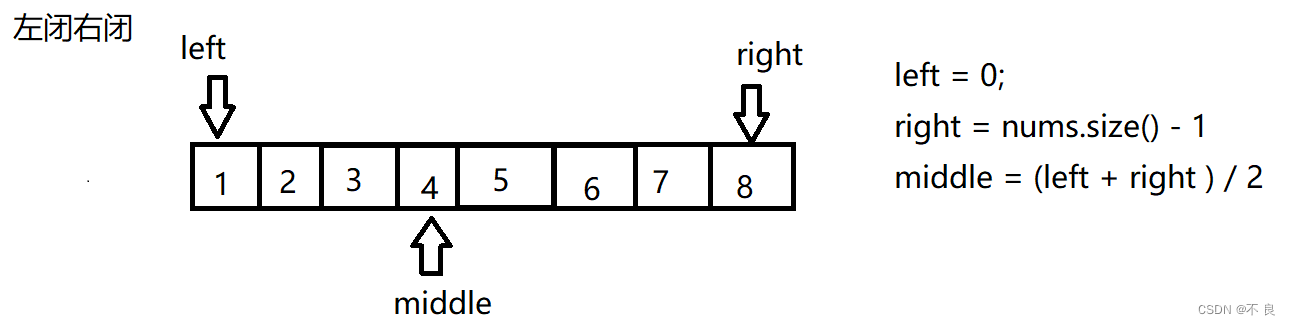
第一种情况:左闭右闭
当我们使用左闭右闭区间的时候,
while(left <= right)是合法的,即left和right能够满足这个条件;
right再次赋值时我们已经判断middle不等于target了,要控制好边界条件,所以要让right = middle-1;当我们写成right = middle时,区间不明确,边界处理的不对,会出问题;left再次赋值时,也不能等于middle,更新右区间里的左边界。
左闭右闭代码如下:
class Solution {
public:
int search(vector<int>& nums, int target) {
int right = nums.size() - 1; //左闭右闭要包含right,所以right = nums.size() - 1
int left = 0;
while(left <= right) //合法情况
{
int middle = (left + right) / 2;
if(nums[middle] > target)
right = middle - 1;//更新左区间里的右边界
else if(nums[middle] < target)
left = middle + 1;//更新右区间里的左边界
else
return middle;
}
return -1;
}
};
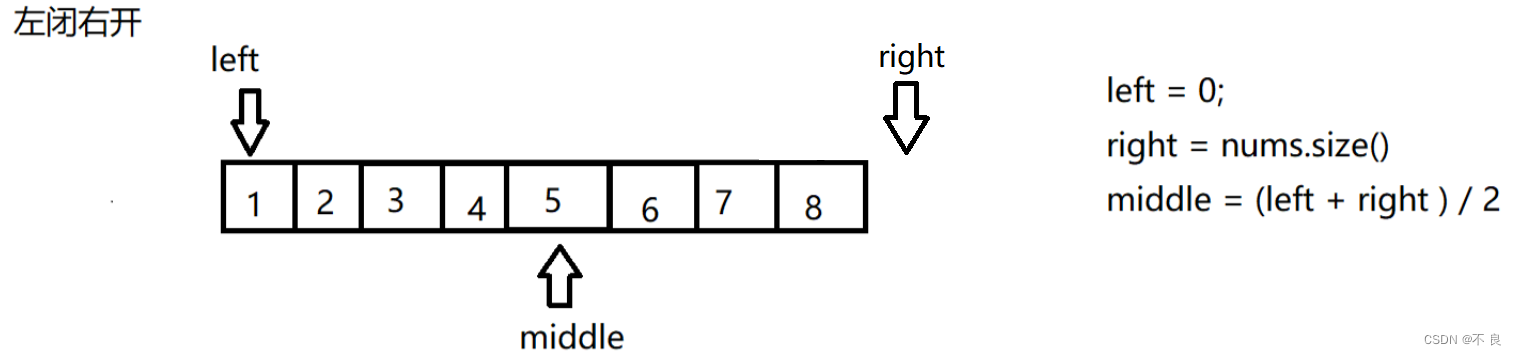
第二种情况:左闭右开
左闭右开区间,
left不能和right相等,所以循环条件应该是while(left < right),根据区间的定义来查询,因为右开不包含right,所以right = middle,更新左区间里的右边界,left更新的时候仍然是left = middle + 1。
左闭右开代码如下:
class Solution {
public:
int search(vector<int>& nums, int target) {
int right = nums.size();//左闭右开不包含right,所以right = nums.size()
int left = 0;
while(left < right) //不能加等于
{
int middle = (left + right) / 2;
if(nums[middle] > target)
right = middle;//更新左区间里的右边界
else if(nums[middle] < target)
left = middle + 1;//更新右区间里的左边界
else
return middle;
}
return -1;
}
};
总结:
左闭右闭区间时,
while的循环条件为left <= right,且right = middle -1;左闭右开区间时,
while的循环条件为left < right,且right = middle;两个区间的
left都是left = middle + 1。
![[架构之路-192]-《软考-系统分析师》-8-软件工程 - 14种UML图快速概览](https://img-blog.csdnimg.cn/247de919746c4b5f856378485039d389.png)