---

1. 冒泡排序

1. 思想
   排升序：每趟将前后两元素进行比较，按照“前小后大”进行交换，将最大的元素放在最后。
   排降序：每趟将前后两元素进行比较，按照“前大后小”进行交换，将最小的元素放在最后。
2. 例子（以排升序为例）
   
3. 代码实现

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
void BubbleSort(int* a, int n)
{
	int flag = 1;
	for (int j = 0; j < n-1; j++)
	{
		//一趟排序
		for (int i = 0; i < n - 1 - j; i++)
		{
			if (a[i] > a[i + 1])
			{
				flag = 0;
				Swap(&a[i], &a[i + 1]);
			}
		}
		if (flag == 1)//如果一趟排序下来，发现根本没发生交换，说明数据本身有序，直接跳出
		{
			break;
		}
	}
}

4. 算法分析
   时间复杂度
   最好情况下是有序，时间复杂度是O（N），最坏情况下是逆序，时间复杂度是O（N^2）。
   空间复杂度
   没额外开辟空间，空间复杂度是O（1）。
   稳定性
   排升序时遇到相同的不交换，只交换前面大于后面的元素。是稳定的排序。

---

2. 快速排序

2.1霍尔版本

1. 思想
   在数据中找一个关键值（key），比如找左边第一个元素，然后通过一些操作将其放在数据中正确的位置（以排升序为例，将比key小的元素放在左边，将比key大的元素放在右边）。这样就将key排序后的位置确定下来。再以key为界限，按照上面的步骤，找出其他数据在排序后的正确位置。

2. 例子
   

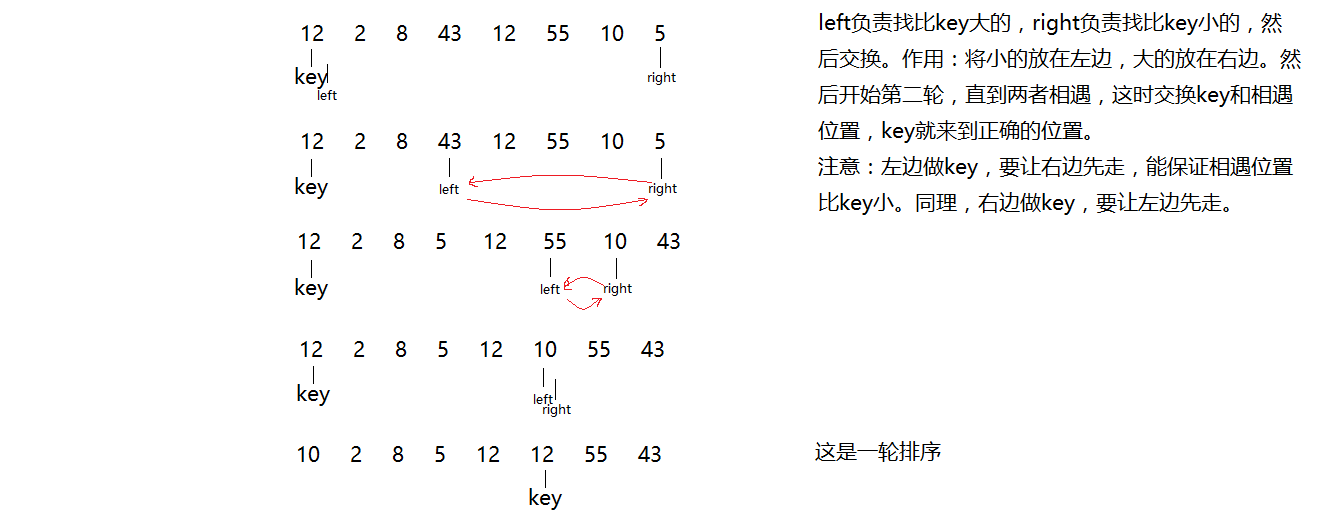
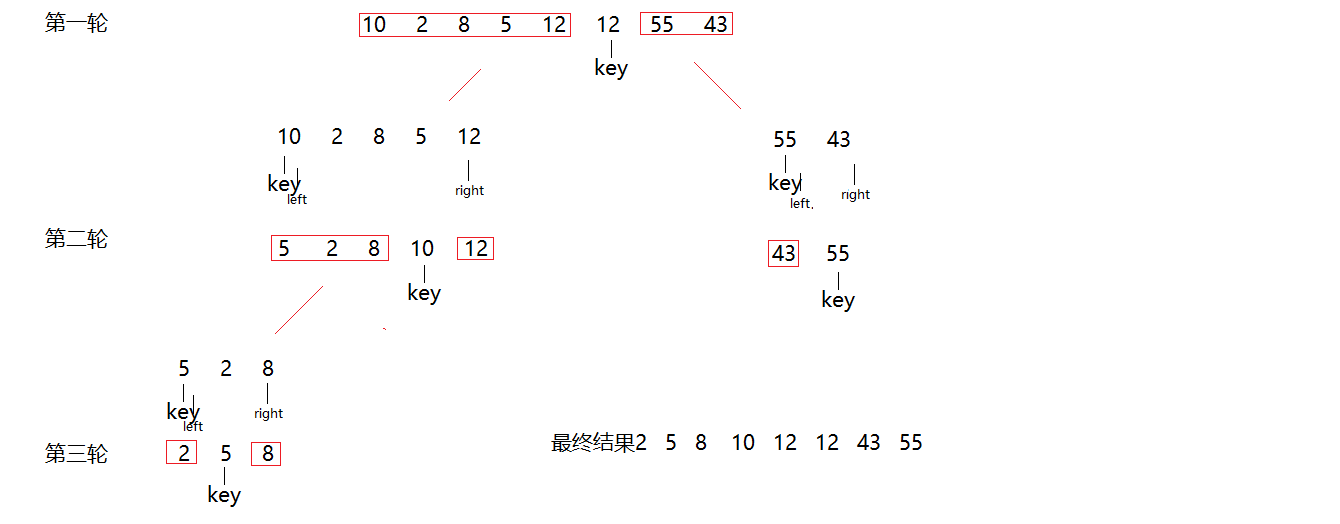
3. 代码实现

//快速排序
void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	int keyi = begin ;//keyi是关键值的下标
	int left = begin ;
	int right = end;
	while (left < right)
	{
		//先右边找小
		while (left<right && a[right] >= a[keyi])
		{
			right--;
		}
		//再左边找大
		while (left<right && a[left] <= a[keyi])
		{
			left++;
		}
		Swap(&a[left], &a[right]);
	}
	Swap(&a[left], &a[keyi]);
	QuickSort(a, begin, left - 1);
	QuickSort(a, left + 1, end);
}

4. 算法分析
   时间复杂度
   最好情况下，是key在数据最中间，左右序列长度相等，这样如果有N个数据，就有logN层，第一层需要遍历N-1个，第二层需要遍历N-3个，所以单趟排序的时间复杂度是O（N），加上一共logN层，时间复杂度是O（NlogN）。
   最坏情况下，是数据本身就有序（顺序或者逆序）。单趟排序的时间复杂度是O（N），一共有N层，时间复杂度是O（N^2）。
   空间复杂度
   最好情况下是O（logN），最会情况下是O（N）。
   稳定性
   数据中存在与key相等的数，但key可能会与其后面的元素交换，所以是不稳定的排序。

5. 优化
   如果出现顺序和逆序情况该怎么办？还是采用快排的方法。主要问题是key的选择。如果key的值是数据的中间值，越接近中心，遍历越像二叉树，深度越像logN，那么快排的效率就是最高的。那如何选出好的key？
   这有两种方法：
   法一：随机选keyi（key的下标）

void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}

	//修改
	int keyi = begin;
	int randi = begin + rand() % (end - begin);
	Swap(&a[randi], &a[keyi]);
	
	int left = begin;
	int right = end;
	while (left < right)
	{
		//先右边找小
		while (left < right && a[right] >= a[keyi])
		{
			right--;
		}
		//再左边找大
		while (left < right && a[left] <= a[keyi])
		{
			left++;
		}
		Swap(&a[left], &a[right]);
	}
	Swap(&a[left], &a[keyi]);
	QuickSort(a, begin, left - 1);
	QuickSort(a, left + 1, end);
}

法二：三数取中

void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}

	//修改
	int keyi = begin;
	int mid = GetMidNumi(a, begin, end);
	Swap(&a[mid], &a[keyi]);

	int left = begin;
	int right = end;


	while (left < right)
	{
		//先右边找小
		while (left<right && a[right] >= a[keyi])
		{
			right--;
		}
		//再左边找大
		while (left<right && a[left] <= a[keyi])
		{
			left++;
		}
		Swap(&a[left], &a[right]);
	}
	Swap(&a[left], &a[keyi]);
	QuickSort(a, begin, left - 1);
	QuickSort(a, left + 1, end);
}

2.2 挖坑法

1. 思想
   先把key提出来，它的位置变成坑。右边找小，找到后把小的放进坑里，左边找打，找到后把大的放进坑里。然后重复以上操作。最终左右相遇，还是相遇在坑里（因为它们中至少有一个是坑）。
2. 例子
   
3. 代码实现

void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	int mid = GetMidNumi(a, begin, end);
	Swap(&a[begin], &a[mid]);
	int key = a[begin];
	int hole = begin;

	int left = begin;
	int right = end;
	while (left < right)
	{
		//右边找小
		while (left < right && a[right] >= key)
		{
			--right;
		}
		a[hole] = a[right];
		hole = right;
		
		//左边找大
		while (left < right && a[left] <= key)
		{
			++left;
		}
		a[hole] = a[left];
		hole = left;
	}
	a[hole] = key;
	QuickSort(a, begin, hole - 1);
	QuickSort(a, hole + 1, end);
}

2.3 前后指针法（最优）

1. 思想
   有prev和cur两个指针。cur找到比key小的值时，++prev，cur和prev位置的值交换，++cur；cur找到比key大的值，++cur。

2. 例子
   

3. 代码实现

void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	int mid = GetMidNumi(a, begin, end);
	Swap(&a[mid], &a[begin]);
	int key = a[begin];

	int prev = begin;
	int cur = prev + 1;
	while (cur <= end)
	{
		if (a[cur] < key && ++prev != cur)
		{
			Swap(&a[cur], &a[prev]);
		}
		++cur;
	}
	Swap(&a[begin], &a[prev]);
	QuickSort(a, begin, prev - 1);
	QuickSort(a, prev + 1, end);
}

2.4 小区间优化

当区间小于某个界限时，不再用递归，用直接插入法。如果最后一层没递归的话，就可以减少一半的递归次数（假设一共递归h层，最后一层要递归2^(h-1)次，总共递归次数为2 ^h-1，所以最后一层的递归次数占一半）。
当区间较小时，不再用递归，改用直接插入，这就是小区间优化。
代码实现

void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	if ((end - begin ) + 1 > 10)//意思是区间元素个数大于10就递归，小于10就直接插入排序
	{
		int mid = GetMidNumi(a, begin, end);
		Swap(&a[mid], &a[begin]);
		int key = a[begin];

		int prev = begin;
		int cur = prev + 1;
		while (cur <= end)
		{
			if (a[cur] < key && ++prev != cur)
			{
				Swap(&a[cur], &a[prev]);
			}
			++cur;
		}
		Swap(&a[begin], &a[prev]);
		QuickSort(a, begin, prev - 1);
		QuickSort(a, prev + 1, end);
	}
	else
	{
		InsertSort(a + begin, end - begin + 1);
	}
}

2.5 非递归快排

当递归层次太深，栈会溢出。这时就得把递归改为非递归。将递归改为非递归一般有两种方法：一是直接改为循环；二是间接改为循环（使用栈辅助）。快速排序改为非递归是用栈辅助。

1. 思想
   首先将数据的两个边界点入栈，然后每次从栈里面取出两个边界点（一段区间），接着单趟排序获得key的下标，以key的下标作为分界点，将边界点重新入栈。当区间只有一个值或者不存在就不需要入栈。

2. 例子
   

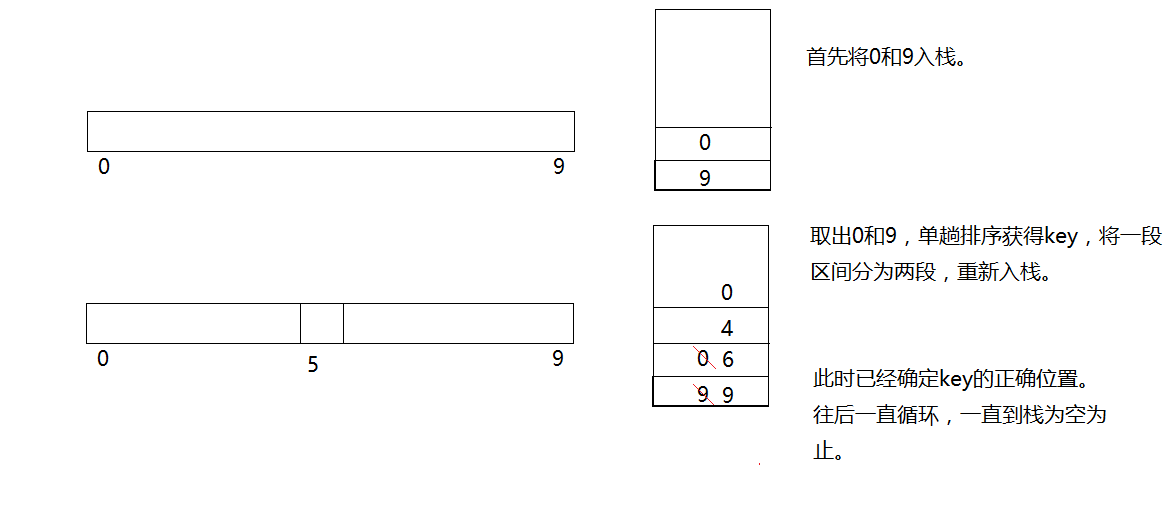
3. 代码实现

int QSort(int* a, int begin, int end)
{
	int mid = GetMidNumi(a, begin, end);
	int keyi = begin;
	Swap(&a[begin], &a[mid]);
	int prev = begin;
	int cur = prev + 1;
	while (cur <= end)
	{
		if (a[cur] < a[keyi] && ++prev != cur)
		{
			Swap(&a[cur], &a[prev]);
		}
		++cur;
	}
	Swap(&a[keyi], &a[prev]);
	return prev;
}
void QuickSortNonR(int* a, int begin, int end)
{
	ST st;
	STInit(&st);
	//将区间入栈
	STPush(&st, end);//注意入栈的顺序，这里统一先用右边界点入栈
	STPush(&st, begin);//出栈时统一先用左边界点接收
	while (!STEmpty(&st))
	{
		int left = STTop(&st);
		STPop(&st);
		int right = STTop(&st);
		STPop(&st);
		//单趟排序
		int keyi = QSort(a, left, right);//将前后指针法得到key封装成一个函数
		//现在有两段子区间，[left,keyi-1][keyi+1,right]
		//判断是否达到入栈条件：子区间元素个数>1
		if (keyi + 1 < right)
		{
			STPush(&st, right);
			STPush(&st, keyi+1);
		}
		if (left < keyi - 1)
		{
			STPush(&st, keyi - 1);
			STPush(&st, left);
		}
	}
	STDestroy(&st);
}