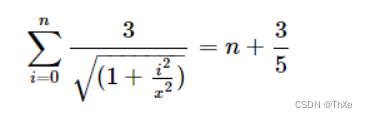比赛记录:Codeforces Round 871 (Div. 4) A~H

news2024/11/25 22:51:25

传送门:CF

A题:A. Love Story

简单比对一下即可解决

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {
	ll x=0,w=1;char ch=getchar();
	for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;
	for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
	return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define	int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int main() {
	int T=read();
	while(T--) {
		string s="codeforces";
		string k;cin>>k;
		int ans=0;
		for(int i=0;i<s.length();i++) {
			if(s[i]!=k[i]) ans++;
		}
		cout<<ans<<endl;
	}
	return 0;
}

B题:Blank Space

记录最大的连续0的个数,循环模拟即可

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {
	ll x=0,w=1;char ch=getchar();
	for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;
	for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
	return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define	int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int a[maxn];
int main() {
	int T=read();
	while(T--) {
		int n=read();
		for(int i=1;i<=n;i++) {
			a[i]=read();
		}
		int maxx=0;int len=0;
		for(int i=1;i<=n;i++) {
			if(a[i]==0) {
				len++;
			}
			else {
				maxx=max(maxx,len);
				len=0;
			}
		}
		maxx=max(maxx,len);
		cout<<maxx<<endl;
	}
	return 0;
}

C题:Mr. Perfectly Fine

字符串或运算之后存在"11".考虑记录"01""11""10"各自的最小花费,那么最终的答案就是min(“01”+“10”,“11”).直接输出即可

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {
	ll x=0,w=1;char ch=getchar();
	for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;
	for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
	return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define	int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int main() {
	int T=read();
	while(T--) {
		int n=read();
		int min1=int_INF,min2=int_INF,min3=int_INF;
		for(int i=1;i<=n;i++) {
			int num=read();string s;cin>>s;
			if(s=="00") continue;
			else if(s=="01") min1=min(min1,num);
			else if(s=="11") min2=min(min2,num);
			else if(s=="10") min3=min(min3,num);
		}
		if(min(min1+min3,min2)>=int_INF) cout<<-1<<endl; 
		else cout<<min(min1+min3,min2)<<endl;
	}
	return 0;
}

D题:Gold Rush

容易看出每一次操作就是得到 n / 3 , n ∗ 2 / 3 n/3,n*2/3 n/3,n∗2/3.问最后是否能得到m.考虑倒过来思考,就是对 m m m进行反操作,每次得到 m ∗ 3 , m ∗ 1.5 m*3,m*1.5 m∗3,m∗1.5问最后是否能得到 n n n
考虑使用map的性质来进行死循环式的枚举.因为map是自带从小到大排序的,并且我们每一次进行乘法显然也是单调增的.所以恰好可以利用这个性质.只要我们最终的map中出现n,那么显然是直接输出"Yes".但是此时我们的遍历时死循环的.所以我们需要考虑一下边界.显然当我们当前枚举到的值大于 n n n的时候便没必要继续下去了

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {
	ll x=0,w=1;char ch=getchar();
	for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;
	for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
	return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define	int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
map<int,int>mp;
int main() {
	int T=read();
	while(T--) {
		int n=read(),m=read();
		mp.clear();
		int minn=m;mp[m]=1;
		for(auto it : mp) {
			mp[it.first*3]=1;
			minn=max(it.first,minn);
			if(it.first*3%2==0) {
				mp[it.first*3/2]=1;
				minn=max(it.first*3/2,minn);
			}
			if(mp[n]) {
				cout<<"YES"<<endl;
				break;
			}
			if(minn>n) {
				cout<<"NO"<<endl;
				break;
			}
		}
	}
	return 0;
}

E题:The Lakes

简单染色题.对于每一个联通块进行染色并且累计一下贡献即可.在本题中使用 d f s dfs dfs并不会爆栈,所以直接使用 d f s dfs dfs即可
假设不会染色题,建议直接搜索一下对应的知识,网上对此有大量的介绍,此处就不在赘述了

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {
	ll x=0,w=1;char ch=getchar();
	for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;
	for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
	return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define	int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int mp[2000][2000];
int vis[2000][2000];
int dx[4]={1,0,-1,0};
int dy[4]={0,-1,0,1};
int n,m;int sum=0;
void dfs(int x,int y) {
	for(int i=0;i<4;i++) {
		int nx=x+dx[i],ny=y+dy[i];
		if(nx<1||nx>n||ny<1||ny>m||mp[nx][ny]==0||vis[nx][ny]) continue;
		vis[nx][ny]=1;
		sum+=mp[nx][ny];
		dfs(nx,ny);
	}
}
int main() {
	int T=read();
	while(T--) {
		n=read(),m=read();
		for(int i=1;i<=n;i++) {
			for(int j=1;j<=m;j++) {
				mp[i][j]=read();
				vis[i][j]=0;
			}
		}
		int ans=0;
		for(int i=1;i<=n;i++) {
			for(int j=1;j<=m;j++) {
				if(!vis[i][j]&&mp[i][j]!=0) {
					vis[i][j]=1;
					sum=mp[i][j];
					dfs(i,j);
					ans=max(ans,sum);
				}
			}
		}
		cout<<ans<<endl;
	}
	return 0;
}

F题:Forever Winter

发现最终的只有边界的雪花顶点的入度是唯一的(考虑存无向边,那么入度等于出度的),并且入度只能是1.所以从这个开始入手.
先存下每一个点的入度.那么找到入度为1的点,这个点就是边界的那个点.这个点有一个唯一的邻接点(记为u),不难发现 i n [ u ] − 1 in[u]-1 in[u]−1就是我们其中的一个答案.并且我们还会发现对于u的所有邻接点v中,只有当v为雪花的顶点时入度是不等于1的.所以我们不难找到雪花的顶点.

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {
	ll x=0,w=1;char ch=getchar();
	for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;
	for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
	return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define	int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int in[maxn];
vector<int>edge[maxn];
int main() {
	int T=read();
	while(T--) {
		int n=read(),m=read();
		for(int i=1;i<=n;i++) {
			edge[i].clear();
			in[i]=0;
		}
		for(int i=1;i<=m;i++) {
			int u=read(),v=read();
			edge[u].push_back(v);
			edge[v].push_back(u);
			in[u]++;in[v]++;
		}
		int ans1=0,ans2=0;
		for(int i=1;i<=n;i++) {
			if(in[i]==1) {
				ans1=in[edge[i][0]]-1;
				int u=edge[i][0];
				for(int j=0;j<edge[u].size();j++) {
					int v=edge[u][j];
					if(in[v]!=1) {
						ans2=in[v];
					}
				}
				break;
			}
		}
		cout<<ans2<<" "<<ans1<<endl;
	}
	return 0;
}

G题:G. Hits Different

本题我是纯纯的使用数列的递推的方法解决的.应该是属于较麻烦的那一类.
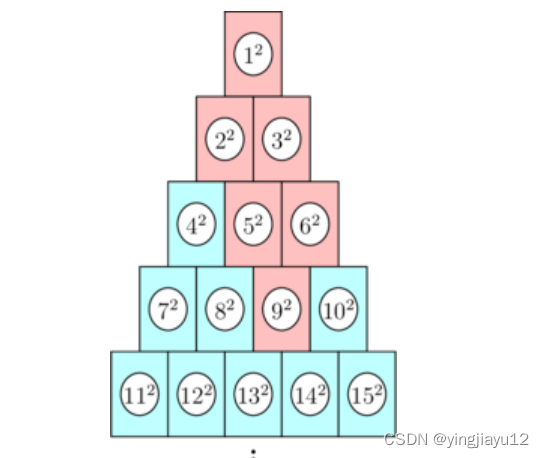
在这里插入图片描述
不难发现,当我们的数字是可以由之前的数字递推而来的.更为详细的来说:
我们的当前的数字的贡献可以由他的正上方的两个数字进行递推而来,举个栗子:
当前数字等于8:此时我们由4和5递推而来
当前数字等于7,此时因为7处于边界状态,所以有一个数字不存在,那么就直接由4递推而来
但是此时需要注意的是,我们的 F ( 8 ) ! = F ( 4 ) + F ( 5 ) + 8 ∗ 8 F(8)!=F(4)+F(5)+8*8 F(8)!=F(4)+F(5)+8∗8,我们此时发现会存在重复,并且不难发现此时重复的值就是 F ( 2 ) F(2) F(2)(也就是跨一行的正上方).
那么对于每一个点,我们都找到对应的递推点以及重复点即可(具体方法此处就不在赘述了,找起来也并不麻烦,可以参考代码)

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {
	ll x=0,w=1;char ch=getchar();
	for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;
	for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
	return x*w;
}
#define int long long
#define maxn 1000010
const double eps=1e-8;
#define	int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int num[maxn];
signed main() {
	int T=read();
	num[1]=1;int cnt=1;int len=1;
	for(int i=2;i<=1e6+10;i++) {
		if(cnt==1) num[i]=i*i+num[i-len];
		else if(cnt==len+1) num[i]=i*i+num[i-len-1];
		else {
			num[i]=i*i+num[i-(len+1)]+num[i-(len+1)+1];
			int k=i-(len+1);
			if(cnt-1==1) num[i]-=num[k-(len-1)];
			else {
				num[i]-=num[k-(len)+1];
			}
		}
		cnt++;
		if(cnt>len+1) cnt=1,len++;
	}
	while(T--) {
		int n=read();
		cout<<num[n]<<endl;
	}
	return 0;
}

H题:Don’t Blame Me

发现我们的最终的状态很小.并且我们最后需要的是每一个状态的贡献.所以在实现的过程中显然可以枚举每一个贡献.刚开始我想的方案是可以记录每一个数字在我们最终序列中的贡献(考虑拆位记录,使用组合数统计)(这个想法很符合CF的出题尿性),但是真正实现过程中感觉很麻烦.然后赛时队友提出了 d p dp dp的想法.感觉很对.
考虑使用 d p [ i ] [ s ] dp[i][s] dp[i][s]来记录前 i i i位可以形成最终状态为 s s s的子序列个数.不难发现递推方式:
当前数字可以选择使用或者不使用:
1.如果不使用,那么对之前的状态没有影响,此时 d p [ i ] [ s ] + = d p [ i − 1 ] [ s ] dp[i][s]+=dp[i-1][s] dp[i][s]+=dp[i−1][s]
2.如果考虑使用,那么此时我们可以对之前所有存在的 s s s进行 a n d and and运算,也就是 d p [ i ] [ s & a [ i ] ] + = d p [ i − 1 ] [ s ] dp[i][s\&a[i]]+=dp[i-1][s] dp[i][s&a[i]]+=dp[i−1][s]
最后只要每一个符合的状态 s s s然后累加贡献即可(本题若想到计数dp,则并不难实现)

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {
	ll x=0,w=1;char ch=getchar();
	for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;
	for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
	return x*w;
}
#define int long long
const int mod=1e9+7;
#define maxn 1000000
const double eps=1e-8;
#define	int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int a[maxn];
int dp[200010][1<<7];
signed main() {
	int T=read();
	while(T--) {
		int n=read(),k=read();
		for(int i=1;i<=n;i++) {
			a[i]=read();
		}
		for(int i=1;i<=n;i++) {
			for(int s=0;s<(1<<6);s++) {
				dp[i][s]=0;
			}
		}
		dp[1][a[1]]=1;
		for(int i=2;i<=n;i++) {
			dp[i][a[i]]=(dp[i][a[i]]+1)%mod;
			for(int s=0;s<(1<<6);s++) {
				dp[i][s]=(dp[i][s]+dp[i-1][s])%mod;
				dp[i][s&a[i]]=(dp[i][s&a[i]]+dp[i-1][s])%mod;
			}
		}
		int ans=0;
		for(int s=0;s<(1<<6);s++) {
			int temp=s;int cnt=0;
			while(temp) {
				cnt+=temp%2;
				temp/=2;
			}
			if(cnt==k) {
				ans=(ans+dp[n][s])%mod;
			}
		}
		cout<<ans<<endl;
	}
	return 0;
}












今日迷思:
曾经不只有一次想过算法竞赛这个东西到底有没有意义,自从接触这个算法竞赛以来,我花了初三的时间,花了高中三年的时间,现在到了大学,还在苦逼的坚持.说真的,为了打算法竞赛真的感觉自己失去了很多.高中一起相约大学打ACM的同学也感觉慢慢的在淡出,他们上各类OJ的时间间隔越来越长,有时候不禁真的在想:还有必要继续坚持下去吗.
但是这场比赛的H题,我最后是在赛后一分钟实现了AC代码,当时时间处于凌晨一点钟,我只能说这种紧张,懊悔+快乐的混杂情感可能是我不打算法竞赛永远体会不到的.可能这就是继续坚持下去的意义吧.不是为了成绩,不是为了别人,而是为了那短暂的快乐.
希望之后的自己会感谢现在充满了负面情绪在悬崖边坚持的自己.

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/499173.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

模拟银行账户转账业务

模拟银行账户转账业务

文章目录 一、需求分析二、核心代码1. 业务层添加 Spring 事务管理2. 配置类中设置事务管理器3. 开启注解式事务驱动 三、相关截图 一、需求分析 需求&#xff1a; 实现任意两个账户间转账操作&#xff0c;要求当转账过程出现异常时&#xff0c;转账方与被转账方的转账操作同时…
阅读更多...
操作系统笔记--CPU调度

操作系统笔记--CPU调度

1--基本概念 CPU调度&#xff1a; 从进程的就绪队列中挑选一个进程/线程作为CPU将要运行的下一个进程/线程&#xff1b; 在下图中&#xff0c;进程产生状态转换时&#xff08;运行→结束、运行→等待&#xff0c;等等&#xff09;都会发生相应的CPU调度&#xff1b; 内核运行调…
阅读更多...
2023/5/7周报

2023/5/7周报

目录 摘要 论文阅读 1、标题和现存问题 2、循环神经网络和传统 LSTM 3、堆叠 LSTM和论文模型结构 4、实验准备 5、结果分析 深度学习 1、TGCN 2、公式 3、伪代码 总结 摘要 本周在论文阅读上&#xff0c;阅读了一篇基于注意力机制的堆叠LSTM心电预测算法的论文。模…
阅读更多...
1 Python数据分析概况

1 Python数据分析概况

1 Python数据分析概况 1.1 认识数据分析1.2 熟悉Python数据分析的工具Python数据分析常用类库 1.3 Jupyter Notebook 快捷键 1.1 认识数据分析 数据分析是指用适当的分析方法对收集来的大量数据进行分析&#xff0c;提取有用信息和形成结论&#xff0c;对数据加以详细研究和概…
阅读更多...
C语言刷题（1）----指针数组

C语言刷题（1）----指针数组

下面指针选题来源于教材、牛客网。 1.键盘输入一个字符串&#xff0c;编写代码获取字符串的长度并输出&#xff0c;要求使用字符指针实现。 示例&#xff1a; 输入&#xff1a; helloworld 返回值&#xff1a; 10 代码实现 #include<stdio.h> int main (void) {char st…
阅读更多...
117-Linux_数据库_事务

117-Linux_数据库_事务

事务 一.什么是事务?二.事务的四大特性1.原子性(atomicity)2.一致性(consistency)3.隔离性(isolation)4.持久性(durability) 三.隔离级别1.READ UNCOMMITTED 未提交读2.READ COMMITTED 提交读3.REPEATABLE READ 可重复读4.SERIALIZABLE 可串行化5.查看隔离级别(1)查看当前会话…
阅读更多...
HTML5 FormData 方法介绍

HTML5 FormData 方法介绍

XMLHttpRequest 是一个浏览器接口&#xff0c;通过它&#xff0c;我们可以使得 Javascript 进行 HTTP (S) 通信。XMLHttpRequest 在现在浏览器中是一种常用的前后台交互数据的方式。2008年 2 月&#xff0c;XMLHttpRequest Level 2 草案提出来了&#xff0c;相对于上一代&#…
阅读更多...
MySQL之约束讲解

MySQL之约束讲解

1. 主键约束 主键约束要求列的数据唯一&#xff0c;并且不能为空。 主键能够唯一地标识表中的一条记录。 主键和记录之间的关系如同身份证和人之间的关系&#xff0c;它们之间是一一对应的。 1.1 单字段主键 直接在定义列的时候指定主键即可。 create table temp1( num int …
阅读更多...
高通 Android 13 兼容extfat模式

高通 Android 13 兼容extfat模式

Android本身不支持extfat格式 需要通过nofuse 打kernel补丁方式去实现 1、kernel/msm-4.19/arch/arm64/configs/vendor/device-perf_defconfig 增加 diff --git a/kernel/msm-4.19/arch/arm64/configs/vendor/device-perf_defconfig b/kernel/msm-4.19/arch/arm64/configs/ve…
阅读更多...
导航栏模糊背景 out 了? 来看看这种模糊是否合你胃口? 并且学习 backdrop-filter

导航栏模糊背景 out 了? 来看看这种模糊是否合你胃口? 并且学习 backdrop-filter

导航栏模糊背景 out 了? 来看看这种模糊是否合你胃口? 并且学习 backdrop-filter 传统情况模糊导航栏效果 &#x1f19a; 一种比较新的模糊导航栏效果(比如 Element-Plus 官网的导航栏效果, 有些类似密集点阵式) 导航栏要实现这个效果必须设置背景为有透明的颜色并且通过 ba…
阅读更多...
Docker安装常用软件-Apollo

Docker安装常用软件-Apollo

零&#xff1a;apollo概念介绍 官网网站&#xff1a;GitHub - apolloconfig/apollo: Apollo is a reliable configuration management system suitable for microservice configuration management scenarios. gitee网址&#xff1a;mirrors / ctripcorp / apollo GitCode …
阅读更多...
家用电器-电磁炉加热原理及实现

家用电器-电磁炉加热原理及实现

目录 一、历史 二、基本原理 三、电路组成 3.1 控制电路 3.2 电源电路 3.3 电磁线圈及驱动电路 3.4 传感器电路 3.5 散热-风扇 四、电磁炉的核心部件 五、电磁炉特点 5.1 加热速度快 5.2 热效率高 5.3 加热的均匀性 六、国内电磁炉市场 参考资料 一、历史 电磁炉…
阅读更多...
【Python入门】Python的判断语句（if else 语句）

【Python入门】Python的判断语句（if else 语句）

前言 &#x1f4d5;作者简介&#xff1a;热爱跑步的恒川&#xff0c;致力于C/C、Java、Python等多编程语言&#xff0c;热爱跑步&#xff0c;喜爱音乐的一位博主。 &#x1f4d7;本文收录于Python零基础入门系列&#xff0c;本专栏主要内容为Python基础语法、判断、循环语句、函…
阅读更多...
idea调优|maven调优

idea调优|maven调优

一、idea调优 1、idea启动优化 首先打开idea->Help->Edit Custom VM Options 按如下配置调整既有参数&#xff0c;参数数值不固定&#xff0c;需根据开发环境配置适当调整。针对如下配置#号后面的为注释&#xff0c;配置时需删除 # 启动堆大小 -Xms2048m # 最大运行堆…
阅读更多...
SpringCloud-OpenFeign案例实战

SpringCloud-OpenFeign案例实战

关于Spring Cloud Open Feign的介绍可以参考这两篇博客 OpenFeign服务接口调用 使用Feign作为服务消费者 本博客参考gitee开源项目代码&#xff0c;结合自己的理解&#xff0c;记录下微服务场景下的使用。Talk is cheap. Show me the code&#xff01; 一、项目结构 这里使用…
阅读更多...
FJUT第17届校赛题解

FJUT第17届校赛题解

致歉 由于出题人经验不足&#xff0c;给大家带来不好的体验&#xff0c;实在抱歉。在赛中忘记开答疑&#xff0c;发不了公告&#xff0c;发现的问题已经在尽量修补。出现的问题如下&#xff08;均修复&#xff09;&#xff1a; 1.薛薛的简单数学题&#xff0c;没写spj&#xf…
阅读更多...
【Python从入门到进阶】18、文件内容序列化和反序列化操作

【Python从入门到进阶】18、文件内容序列化和反序列化操作

接上篇《17、文件的读写操作》 上一篇我们学习了Python文件对象包含哪些方法&#xff0c;并学习了文件如何进行读、写、定位和删除。本篇我们来学习文件读取及写入数据序列化和反序列化的操作。 一、什么是序列化和反序列化 通过文件操作&#xff0c;我们可以将字符串写入到一…
阅读更多...
【Linux】 OpenSSH_7.4p1 升级到 OpenSSH_8.7p1（亲测无问题，建议收藏）

【Linux】 OpenSSH_7.4p1 升级到 OpenSSH_8.7p1（亲测无问题，建议收藏）

&#x1f341;博主简介 &#x1f3c5;云计算领域优质创作者   &#x1f3c5;华为云开发者社区专家博主   &#x1f3c5;阿里云开发者社区专家博主 &#x1f48a;交流社区&#xff1a;运维交流社区 欢迎大家的加入&#xff01; 文章目录 文章声明前述安装一些必要的命令&…
阅读更多...
MySQL数据库学习（进阶篇）

MySQL数据库学习（进阶篇）

1.存储引擎 1.1 MySQL体系结构 连接层 最上层是一些客户端和链接服务&#xff0c;主要完成一些类似于连接处理、授权认证、及相关的安全方案。服务器也会为安全接入的每个客户端验证它所具有的操作权限。 服务层 第二层家口主要完成大多数的核心服务功能&#xff0c;如SQL接口…
阅读更多...
二挡起步——pythonweb开发Django框架，前端原生+Django后端框架+python网络抓包（代替数据库数据）（附带小案例）

二挡起步——pythonweb开发Django框架，前端原生+Django后端框架+python网络抓包（代替数据库数据）（附带小案例）

大家好&#xff0c;我是csdn的博主&#xff1a;lqj_本人 这是我的个人博客主页&#xff1a; lqj_本人的博客_CSDN博客-微信小程序,前端,python领域博主lqj_本人擅长微信小程序,前端,python,等方面的知识https://blog.csdn.net/lbcyllqj?spm1011.2415.3001.5343哔哩哔哩欢迎关注…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023