致歉
由于出题人经验不足,给大家带来不好的体验,实在抱歉。在赛中忘记开答疑,发不了公告,发现的问题已经在尽量修补。出现的问题如下(均修复):
1.薛薛的简单数学题,没写spj,题面不清晰
2.第K大数(hard)std锅
3.QQ的AC自动机,数据范围和题面不一致
4.人看人,数据弱,本意是想让大家O(n)通过
薛薛的简单数学题
公式化简+二分
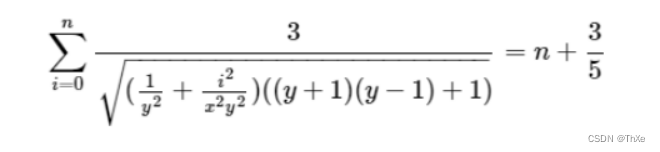
把右边括号里的式子展开,再乘到左边括号中可以得到如下式子:
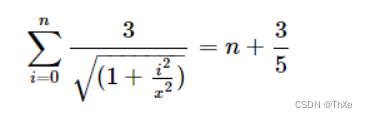
这个式子可以很容易的观察到是一个单调函数,所以x是一个固定的值,用二分求函数的解即能得到
题目要求x+y最小,所以y需要尽可能小,且需要满足是一个整数,根据y的定义域,最小的值为1,(不能取0)
#include<stdio.h>
#include<math.h>
#include<iostream>
using namespace std;
int n;
double f(double x) {
double sum = 0;
for (int k = 0; k <= n; k++)
{
sum += 3 / (sqrt(1 + (double)(k * k) / (x * x)));
}
return (sum > (n + 0.6));
}
double binarySearch(double l, double r) {
double eps = 1e-8; // 精度
while (r - l > eps) {
double mid = (l + r) / 2;
if (f(mid)) {
r = mid;
}
else {
l = mid;
}
}
return l;
}
int main()
{
// freopen("D:\\4773.in","r",stdin);
// freopen("D:\\4773.out","w",stdout);
int t; cin >> t;
while (t--) {
cin >> n;
printf("%.6lf\n", binarySearch(0, 200)+1);
}
//fclose(stdin);
//fclose(stdout);
}
人看人
该题需要使用时间复杂度O(N)的算法
考虑一个长度为n的最优构造为:
若n为偶数左半部全为R,右半部全为L。形如:RRRLLL
若n为奇数,中间一个随意取一个值答案一致。形如: RRRLLLL 或 RRRRLLL
每次只会多增加一个人的转向并且对后续答案不会造成影响。就可以贪心的来选取每次最大价值增加的转向。并且一定是从最左端的L->R或最右端的R->L两种中选取一个,可以使用双指针来比较这两个答案。时间复杂度O(N)
#include<bits/stdc++.h>
using namespace std;
const int N = 2e6 + 10;
typedef long long ll;
int n;
int getR(int i)
{
return n - i - 1;
}
int getL(int i)
{
return i;
}
bool cmp(char a, char b)
{
return a > b;
}
void solve()
{
cin >> n;
string s, per;
cin >> s;
int k = 0;
int L = 0, R = n - 1;
long long ans = 0;
for (int i = 0; i < n; i++)
{
if (s[i] == 'L')ans += i;
else ans += n - i - 1;
}
for (int i = 0; i < n / 2; i++)per += 'R';
for (int i = n / 2; i < n; i++)per += 'L';
//cout << per << endl;
int tans = 0;
for (int i = 0; i < n; i++)
{
if (per[i] == 'L')tans += i;
else tans += n - i - 1;
}
//cout << "tans" << " " << tans << endl;
int l = 0, r = n - 1;
while (l <= r)
{
while (l < n / 2 && s[l] == per[l])l++;
while (r >= n / 2 && s[r] == per[r])r--;
int add1 = getR(l) - getL(l);
int add2 = getL(r) - getR(r);
if (add1 > add2)
{
l++;
if (add1 < 0)continue;
k++;
ans += add1;
cout << ans << " ";
}
else
{
r--;
if (add2 < 0)continue;
k++; ans += add2;
cout << ans << " ";
}
}
while (++k <= n)cout << ans << " ";
cout << endl;
}
int main()
{
//freopen("D:\\1.in","r",stdin);
//freopen("D:\\1.out","w",stdout);
int x;
int t; cin >> t;
while (t--)
{
solve();
}
//fclose(stdin);
//fclose(stdout);
}
旺旺雪饼的宝箱
这题很明显是最短路径的板子题,但题目还要求每次走都得走两步,所以跑最短路径的时候每次都得两个点两个点的遍历,也就是在找离当前点最近点的时候再加一层循环,记录的路径是这次两条路径之和的平方。
/*SPFA*/
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
using namespace std;
struct node{
int to,val;
};
int n,m;
const int N = 1e5+5;
vector<node>vc[N];
int vis[N];
int main(){
cin>>n>>m;
vector<int>ans(N,INF);
while(m--){
int x,y,v;
cin>>x>>y>>v;
vc[x].push_back({y,v});
vc[y].push_back({x,v});
}
ans[1]=0;
queue<int>q;
q.push(1);
vis[1]=1;
while(!q.empty()){
auto cur = q.front();q.pop();
vis[cur]=0;
for(auto& ne1: vc[cur]){
for(auto& ne2:vc[ne1.to]){
if(ne2.to == cur)continue;
if(ans[ne2.to] > ans[cur] + (ne1.val+ne2.val)*(ne1.val+ne2.val)){
ans[ne2.to] = ans[cur] + (ne1.val+ne2.val)*(ne1.val+ne2.val);
if(!vis[ne2.to]){
vis[ne2.to]=1;
q.push(ne2.to);
}
}
}
}
}
for(int i = 1; i <= n; i++){
if(ans[i]==INF)cout<<"no"<<' ';
else cout<<ans[i]<<' ';
}
cout<<'\n';
}
/*DIJ*/
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int n, m;
int h[N], e[N], w[N], ne[N], idx;
void add(int a, int b, int c)
{
w[idx] = c;
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
int st[N], dis[N];
typedef pair<int, int> pii;
void dij()
{
memset(dis, 0x3f, sizeof dis);
priority_queue<pii, vector<pii>,greater<pii>>heap;
dis[1] = 0;
heap.push({ 0,1 });
while (heap.size())
{
auto t = heap.top(); heap.pop();
int wi = t.first, u = t.second;
if (st[u])continue;
st[u] = 1;
for (int i = h[u]; i != -1; i = ne[i])
{
int nj = e[i];
//cout << nj << endl;
for (int j = h[nj]; j != -1; j = ne[j])
{
int now = e[j];
//cout << nj << " " << now << endl;
if (dis[now] > dis[u]+(w[i] + w[j]) * (w[i] + w[j]))
{
dis[now] = dis[u]+(w[i] + w[j]) * (w[i] + w[j]);
heap.push({ dis[now], now });
}
}
}
}
for (int i = 1; i <= n; i++)
{
if (dis[i] != 0x3f3f3f3f)cout << dis[i] << " ";
else cout << "no ";
}
}
int main()
{
memset(h, -1, sizeof h);
cin >> n >> m;
while (m--)
{
int a, b, c; cin >> a >> b >> c;
add(a, b, c);
add(b, a, c);
}
dij();
}
放逐后失水的你
贪心+优先队列
我们可以把路过的加水站看成一个物品,路过它时就把水放到背包里去但是不一定喝,当你无法到达下一站时就喝一瓶价值最大的水。这样可以保证喝水次数最少,用优先队列可以很好的维护这个背包.
#include<bits/stdc++.h>
using namespace std;
const int N = 100005;
int dis[N]; int water[N];
priority_queue<int, vector<int>>heap;
int main()
{
int A, B, n; cin >> A >> B >> n;
for (int i = 1; i <= n; i++)cin >> dis[i];
for (int i = 1; i <= n; i++)cin >> water[i];
int flag = -1, ans = 0, now = B, cnt;
for (cnt = 1; cnt<=n&&now >= dis[cnt]; cnt++)
heap.push(water[cnt]);
if (now < A)
{
while (heap.size())
{
now += heap.top(); heap.pop();
ans++;
while (cnt <= n && now >= dis[cnt])
{
heap.push(water[cnt++]);
}
if (now >= A) {
flag = ans; break;
}
}
}
else flag = 0;
cout << flag << endl;
}
校赛登录速度要快
首先需要找出规律:
题目中给出的条件发现1=A、2=A、4=A
由此联想到二进制中1的个数,再去验证BC,发现是吻合的,DE是用来混淆视听的。
题目中也给出了提示引导着大家往机器码的方向去考虑,不知道是否脑洞太大了呢。
答案的输出方式也需要大家好好的思考不能一次性遇到一个就输出整个字母,首先要记录完整的答案,然后需要每一行每一行的去输出,一共输出9行。
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
//===========================================
const int MAXN = 1e5 + 5;
int a[MAXN];
string num[5][9] = {
{" @ ",
" @ @ ",
" @ @ ",
" @ @ ",
" @ @ ",
" @@@@@@@@@@@ ",
" @ @ ",
" @ @ ",
"@ @ "},
{"@@@@@@@@@@@@@@@ ",
"@ @ ",
"@ @ ",
"@ @ ",
"@@@@@@@@@@@@@@@ ",
"@ @ ",
"@ @ ",
"@ @ ",
"@@@@@@@@@@@@@@@ "},
{"@@@@@@@@@@@@@@@@ ",
"@ ",
"@ ",
"@ ",
"@ ",
"@ ",
"@ ",
"@ ",
"@@@@@@@@@@@@@@@@ "},
{"@@@@@@@@@@@@@@@ ",
"@ @ ",
"@ @ ",
"@ @ ",
"@ @ ",
"@ @ ",
"@ @ ",
"@ @ ",
"@@@@@@@@@@@@@@@ "},
{"@@@@@@@@@@@@@@@ ",
"@ ",
"@ ",
"@ ",
"@@@@@@@@@@@@@@@@ ",
"@ ",
"@ ",
"@ ",
"@@@@@@@@@@@@@@@@ "} };
int temp[1005];
int cnt;
void solve()
{
int n;
cin >> n;
while (n)
{
int res = 0;
int x = n % 10;
n /= 10;
while (x)
{
if (x & 1) res++;
x >>= 1;
}
temp[++cnt] = res;
}
for (int j = 0; j < 9; j++)
{
for (int i = cnt; i > 0; i--)
{
cout << num[temp[i] - 1][j];
}
cout << endl;
}
}
signed main(signed argc, char const* argv[])
{
#ifdef LOCAL
freopen("in.in", "r", stdin);
freopen("out.out", "w", stdout);
#endif
//===========================================
int T = 1;
while (T--)
{
solve();
}
//===========================================
return 0;
}
鞍点数量
暴力签到
#include<bits/stdc++.h>
using namespace std;
int f[1005][1005];
int mx[1005],mi[1005];
int main()
{
int n;
int t;
cin>>n;
for(int i=1;i<=n;i++)
{
t=-1005;
for(int j=1;j<=n;j++)
{
cin>>f[i][j];
if(f[i][j]>t)t=f[i][j];
}
mx[i]=t;
}
for(int i=1;i<=n;i++)
{
t=1005;
for(int j=1;j<=n;j++)
{
if(f[j][i]<t)t=f[j][i];
}
mi[i]=t;
}
int sum=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
if(f[i][j]>=mx[i]&&f[i][j]<=mi[j])sum++;
}
cout<<sum<<endl;
}
QQ的AC自动机
DFS建树,KMP字符串匹配即可
#include <bits/stdc++.h>
#include <utility>
#include <vector>
using namespace std;
string ss;
// kmp求next数组
void get_next(const string &s, vector<int> &next) {
next[0] = -1;
int i = 0, j = -1;
while (i < s.size()) {
if (j == -1 || s[i] == s[j])
next[++i] = ++j;
else j = next[j];
}
}
//kmp 匹配
int kmp(const string &s, const string &t) {
vector<int> next(t.size() + 1);
get_next(t, next);
int i = 0, j = 0, res = 0;
while (i < s.size()) {
if (j == -1 || s[i] == t[j]) {
++i, ++j;
} else j = next[j];
if (j == t.size())
res++, i = i - j, j = -1;
}
return res;
}
void dfs(int u, vector<int> &ans, vector<pair<int, string>> &a) {
if (ans[u] || u == 1) return;
dfs(a[u].first, ans, a);
string &s = a[a[u].first].second;
if (a[u].first == 1) {
ans[u] = ans[1] + kmp("QQ" + a[u].second, ss);
return ;
} else {
ans[u] = ans[a[u].first] +
kmp(s.substr(s.size() - ss.size() + 1, ss.size() - 1) +
a[u].second, ss);
}
}
void solve() {
int n; cin >> n;
cin >> ss;
vector<pair<int, string>> a(n + 1);
a[1] = {-1, "QQ"};
for (int i = 2; i <= n; i++)
cin >> a[i].first >> a[i].second;
vector<int> ans(n + 1);
ans[1] = kmp(a[1].second, ss);
for (int i = 2; i <= n; i++)
dfs(i, ans, a);
for (int i = 1; i <= n; i++)
cout << ans[i] << " ";
cout << endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int t; cin >> t;
while(t--) {
solve();
}
}
第k大数(Easy)
给一个n*m的矩阵求第k大的数
- 暴力
数据范围1000,n方能随便搞。
这你都不会?.jpg
#define int long long
#define rep(i,a,b) for(int i=a;i<=b;i++)
void solve(){
int n,m,k;cin>>n>>m>>k;
vector<int> a(n),b(m);
rep(i,1,n)cin>>a[i-1];
rep(i,1,m)cin>>b[i-1];
vector<int> qwq;
rep(i,1,n)rep(j,1,m)qwq.pb(a[i-1]*b[j-1]);
sort(all(qwq),[&](int a,int b){
return a>b;
});
cout<<qwq[k-1]<<endl;
}
第k大数(Hard)
在上题的基础上,k可能会到1e12级别,并且会有负数
Tag:二分答案+细节处理
先将两个数组排序,求第k大数优先考虑二分答案
假设当前二分的答案为mid,我们需要考虑的是这个n*m的矩阵中有多少数比他大,根据这个去调整二分答案时的左右端点,我们要确保最后二分出来的mid,有k-1个数比它大,或者说>=它的数不少于k个
至于怎么统计矩阵中有多少数比mid大,我们只要去遍历一个数组A,然后根据当前遍历到的数去二分数组B中比 mid/A_i 大的数即可(具体情况要根据正负处理细节),最后对于每个 A_i 统计一遍答案与k作比较即可
二分中的细节实现请看代码
复杂度 O(n log log)
// Duet of Dusk Embers--XrkArul
#include <bits/stdc++.h>
using namespace std;
#define vi vector<int>
#define endl '\n'
#define pb push_back
#define fi first
#define se second
#define all(v) (v).begin(),(v).end()
#define rep(i, a, b) for (int i = a; i <= b; ++i)
#define int long long
signed main() {
ios::sync_with_stdio(0),cin.tie(0);
// freopen("D:\\4.in","r",stdin);
// freopen("D:\\4.out","w",stdout);
int n,m,k;cin>>n>>m>>k;
vi a(n),b(m);
rep(i,1,n)cin>>a[i-1];
rep(i,1,m)cin>>b[i-1];
sort(all(a)),sort(all(b));
int r=1e18+10,l=-r;
int mid;
auto check=[&](int x){
int sum=0;
for(auto y:a){
if(y==0){
if(x<=0)
sum+=m;
continue;
}
int num=x/y;
if(y>0){
if(x%y&&x>=0)num++;
// 找b中大于等于num的个数
int cnt=lower_bound(all(b),num)-b.begin();
sum+=m-cnt;
}else{
if(x%y&&x>=0)num--;
// 找b中小于等于num的个数
int cnt=upper_bound(all(b),num)-b.begin()-1;
sum+=cnt+1;
}
}
return sum>=k;
};
while(l+1<r){
mid=l+r>>1;
if(check(mid))l=mid;
else r=mid;
}
cout<<l<<endl;
// fclose(stdin);
// fclose(stdout);
}
/*
3 3 2
3 -3 0
3 3 4
*/
穹批?星奴!
q次询问,每次问长度为n,每个数的值域在1~x之间的非严格升序数组有多少个
数据范围 1e5
Tag:数学、组合数
这题难在问题比较抽象,我们可以将题目意思转化为典型球盒模型:
n个球放进x个盒子里的方案数,允许空盒,n个球必须放完
听过球盒模型的到这里就结束了,没听过的解释一下:
-
先来介绍n个球放进x个盒子不允许空盒的情况:
用插板法,n 个球中总共有 n-1 个空隙,根据条件,我们只需要在 n−1 个空隙中插 x-1 个板子即可,就完成了将n个求放进x个盒子里,这样的答案是 C(n−1,x−1)
-
允许空盒:
我们可以多加 x 个“虚”的球,预先塞进每个盒子
这样问题就化归成了有 n+x 个球和 x 个不同的盒子,不允许有空盒的情况,直接运用上面的结论就可以解决问题了,答案为 C(n+x−1,x−1)
快速幂+逆元处理组合数, 注意处理到2e5,因为n+x可能会越界
复杂度 O(max(q,n+x))
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const double pi=acos(-1);
#define pii pair<int,int>
#define pll pair<ll, ll>
#define vi vector<int>
#define rep(i, a, b) for (int i = a; i <= b; i++)
#define int long long
const int N = 2e5+10;
const int mod = 1e9+7;
ll f[N],inff[N];
ll imp(ll a,ll k,ll q){
ll res = 1;
while(k){
if(k&1) res = res * a % q;
a = a * a % q;
k >>= 1;
}
return res;
}
void init(){
f[0] = inff[0] = 1;
for(int i = 1;i < N;i ++){
f[i] = f[i - 1] * i % mod;
inff[i] = inff[i - 1] * imp(i, mod - 2, mod) % mod;
}
}
ll C(ll a,ll b){
if(a==b)return 1;
if(a<b)return 0;
return f[a]*inff[b]%mod*inff[a-b]%mod;
}
void solve(){
int n,x;cin>>n>>x;
cout<<C(n+x-1,x-1)<<endl;
}
signed main() {
ios::sync_with_stdio(0),cin.tie(0);
init();
int q;cin>>q;
while(q--)solve();
}
谎言即是爱
给定一个长度为N的序列A,q次询问,每次询问给定 [l,r] 表示区间左右端点。对于每次询问,求出对于任意的x, ∑| x-Ai | 的最小值(l<=i<=r),输出x和该最小值。
Tag:莫队值域分块、主席树
先来思考如何确定x使得 ∑| x-Ai | (l<=i<=r)最小
假设这(r-l+1)个数已经从小到大排好了序,那么问题就转化成了最小化曼哈顿距离
先说结论:满足上式最小的x即为序列的中位数(想看证明的自己去了解)
对于长度为偶数的序列,也可以是从小到大中间的那两个数
那么知道这个结论之后,这题就是个典题了:
先找到中位数,然后求出所有比中位数小的数的和、比中位数大的和,最后计算即可
该过程的维护可以利用各种数据结构实现(主席树、莫队)
这边主要讲一下莫队结合值域分块去乱搞这一类题
莫队算法主要用来处理离线的区间询问问题(点击这里学习)
而分块是一种好用好写且十分暴力的思想,不仅仅是数据结构,它在图论和树论还有数论中都有较为广泛的应用(根号分治:去年CCPC绵阳G),但一般情况下长为1e6的序列就会炸掉,1e5级别比较不容易炸
将这两个东西结合起来,就能完美地解决该题。我们先将数离散化让他们的值域从1e9降为1e5,然后我们就可以分为sqrt(1e5)个块,要找到该值域内的中位数,维护每个块中现有数的个数,然后只需要暴力遍历每个块即可(增删数的同时对应块中现有数的个数也要修改),这样做的话最多只要遍历sqrt(1e5)+sqrt(1e5)次就能找到中位数(其实第k大的数也是同理)
至于统计比x 小/大 的数的和,同样维护每个块内的和,然后暴力遍历每个块把和加上即可
题解写的比较匆忙,关于莫队值域分块有不懂的地方欢迎找我讨论
代码实现不尽相同,下面两个版本仅供参考。
虽然主席树跑得快点,但是分块的适用性更广,并且想起来比较无脑,这一点你们在今后的做题中会感受到的(
莫队值域分块:
// Duet of Dusk Embers--XrkArul
#include <bits/stdc++.h>
using namespace std;
#define vi vector<int>
#define endl '\n'
#define pb push_back
#define fi first
#define se second
#define all(v) (v).begin(),(v).end()
#define rep(i, a, b) for (int i = a; i <= b; ++i)
#define int long long
int block;//块的长度
struct node {
int l, r, id;
bool operator<(const node &x) const {
if (l / block != x.l / block) return l < x.l;
if ((l / block) & 1)return r < x.r;
return r > x.r;
}
};
void solve(){
int n;cin>>n;
vi a(n+1),pos(n+1);//pos 用于离散化映射a数组
map<int,int> mp;
rep(i,1,n)cin>>a[i],mp[a[i]]=1;
int id=0;
vi zhi(n+1);// 第i小的数对应的a[i]
for(auto &x:mp){
x.se=++id;
zhi[x.se]=x.fi;
}
rep(i,1,n)pos[i]=mp[a[i]];//离散化a
int q;cin>>q;
vector<pair<int,int>> ans(q+1);
block=sqrt(n);
vector<node> qr;//把询问离线
rep(i,1,q){
int l,r;cin>>l>>r;
qr.pb({l,r,i});
}
sort(all(qr));
vi cnt_sum(n+1);// 存每个值域块内数的个数
vi cnt_cnt(n+1);// 存每个值域数的个数(可能有多个值相同的数,这个时候对应值域的个数要累加)
vi sum(n+1);// 存每个值域块内所有数的和
auto getid=[&](int x){// 获取当前数在第几个块
return x/block;
};
auto add=[&](int x){//莫队增数操作
cnt_sum[getid(pos[x])]++;
sum[getid(pos[x])]+=a[x];
cnt_cnt[pos[x]]++;
};
auto del=[&](int x){//莫队删数操作
cnt_sum[getid(pos[x])]--;
sum[getid(pos[x])]-=a[x];
cnt_cnt[pos[x]]--;
};
auto query=[&](node x){
int num=x.r-x.l+1;
num=(num+1)/2;//找第num个数(即中位数)
int num_1=num;
int res=0;// 和
int mid=-1;
for(int i=0;block*i<=n;i++){
if(mid!=-1){//已经找到中位数了
res+=sum[i];
res-=cnt_sum[i]*zhi[mid];
continue;
}
if(num>cnt_sum[i]){
num-=cnt_sum[i];
res-=sum[i];
continue;
}
int l=i*block,r=min(n,l+block-1);//当前块的左右端点
rep(j,l,r){
if(mid!=-1){// 已经找到中位数了,这时候就统计比x大的数的贡献
res+=cnt_cnt[j]*(zhi[j]-zhi[mid]);
continue;
}
if(num>cnt_cnt[j])num-=cnt_cnt[j],res-=cnt_cnt[j]*zhi[j];
else{
mid=j;
res+=zhi[mid]*(num_1-num);//把前面|mid-x|漏掉的mid补回来
}
}
}
return {mid,res};
};
int l=1,r=0;
for(auto x:qr){// 莫队
while(l<x.l)del(l++);
while(r>x.r)del(r--);
while(l>x.l)add(--l);
while(r<x.r)add(++r);
ans[x.id]=query(x);
}
rep(i,1,q)cout<<zhi[ans[i].fi]<<" "<<ans[i].se<<endl;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
solve();
return 0;
}
主席树代码:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <vector>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
struct Node
{
int l, r, cnt;
ll sum;
}tr[N * 25];
int n, m;
int w[N];
ll s[N];
vector<int> alls;
int root[N], idx;
int get(int x)
{
return lower_bound(alls.begin(), alls.end(), x) - alls.begin() + 1;
}
void build(int& x, int l, int r)
{
x = ++ idx;
if (l == r) return ;
int mid = (l + r) >> 1;
build(tr[x].l, l, mid);
build(tr[x].r, mid + 1, r);
}
void modify(int p, int& q, int l, int r, int id)
{
q = ++ idx;
tr[q] = tr[p];
tr[q].cnt ++;
tr[q].sum += alls[id - 1];
if (l == r) return ;
int mid = (l + r) >> 1;
if (id <= mid) modify(tr[p].l, tr[q].l, l, mid, id);
else modify(tr[p].r, tr[q].r, mid + 1, r, id);
}
int query1(int p, int q, int l, int r, int k)
{
if (l == r) return alls[l - 1];
int s = tr[tr[q].l].cnt - tr[tr[p].l].cnt;
int mid = (l + r) >> 1;
if (k <= s) return query1(tr[p].l, tr[q].l, l, mid, k);
else return query1(tr[p].r, tr[q].r, mid + 1, r, k - s);
}
ll query2(int p, int q, int l, int r, int x)
{
if (l == r) return 0;
int mid = (l + r) >> 1;
if (x <= alls[mid - 1]) return (tr[tr[q].r].sum - tr[tr[p].r].sum - (ll)(tr[tr[q].r].cnt - tr[tr[p].r].cnt) * x) + query2(tr[p].l, tr[q].l, l, mid, x);
else return query2(tr[p].r, tr[q].r, mid + 1, r, x) + ((ll)(tr[tr[q].l].cnt - tr[tr[p].l].cnt) * x - (tr[tr[q].l].sum - tr[tr[p].l].sum));
}
int main()
{
cin >> n;
for (int i = 1; i <= n; i ++ )
{
cin >> w[i];
alls.push_back(w[i]);
s[i] = s[i - 1] + w[i];
}
sort(alls.begin(), alls.end());
alls.erase(unique(alls.begin(), alls.end()), alls.end());
build(root[0], 1, alls.size());
for (int i = 1; i <= n; i ++ ) modify(root[i - 1], root[i], 1, alls.size(), get(w[i]));
cin >> m;
int l, r;
while (m -- )
{
cin >> l >> r;
int k = (r - l + 1 + 2 - 1) / 2;
int x = query1(root[l - 1], root[r], 1, alls.size(), k);
cout << query2(root[l - 1], root[r], 1, alls.size(), x) << endl;
}
return 0;
}
永远是深夜有多好
初始给一个空图,有m个三元组,对于这 m 个三元组,如果存在 i 满足条件:ai 和bi 不在同一个连通块,并且 (ai 所在连通块的点权和)+(bi 所在连通块的点权和)≥ si 。
那么输出最小的 i ,并且在 ai 和bi 间连一条无向边。
否则,结束程序
输出操作的结果
Tag:启发式合并堆、折半处理思想
因为题面要求的是输出满足条件的最小 i ,我们选择用堆去从小到大维护满足条件的 i 并模拟上述程序的过程
在检查第 i 个三元组是否满足条件时,我们需要重点考虑的是如果两个连通块的点权和小于 s[i] 该怎么处理,这也是本题最难想到的点
很多人可能就这么写了:
pq[f1].push({err-sum[f2],i});
pq[f2].push({err-sum[f1],i});
这是经典的错误,因为这样就只关注了一个连通块权值的变化,而忽略了另一个连通块权值的增加
那要怎么处理呢?
我们知道如果a+b>=s,那么a和b中至少有一个 ≥ s/2
基于这个思想,我们可以把两个连通块的点权和与 s[i] 的差值折半,分别放进两个连通块的堆:
int err=(s[i]-sum[f1]-sum[f2]+1)/2;// 折半,+1是为向上取整
pq[f1].push({err+sum[f1],i});
pq[f2].push({err+sum[f2],i});
不难发现,对于单个差值,我们放进堆的次数是log级别的
接下来就是考虑两个连通块合并时,它们堆的合并,学过启发式合并(不懂的点这里,严格鸽讲很细)的都知道,从小堆合并到大堆,总的元素操作次数是log级别的
这样一来,只要在一边维护各个连通块的堆的同时一边检查满足条件的三元组即可完成本题
理论复杂度O(nlogloglog),实际跑的飞快
#include <bits/stdc++.h>
using namespace std;
#define vi vector<int>
#define endl '\n'
#define pb push_back
#define fi first
#define se second
#define pii pair<int, int>
#define rep(i, a, b) for (int i = a; i <= b; ++i)
#define int long long
int fa[200005],sum[200005];
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
void hb(int x,int y){// 并查集维护连通块和
int p=find(x),q=find(y);
if(p==q)return;
fa[p]=q;
sum[q]+=sum[p];
}
void solve(){
int n,m;cin>>n>>m;
vi w(n+1),a(m+1),b(m+1),s(m+1);
rep(i,1,n)cin>>w[i];
rep(i,1,n)fa[i]=i,sum[i]=w[i];
priority_queue<int,vi,greater<int>> q;// 维护满足条件的i
priority_queue<pii,vector<pii>,greater<pii>> pq[n+1];// 维护每个连通块中不满足条件时需要满足的折半临界值
auto update=[&](int i){// 检查i
int f1=find(a[i]),f2=find(b[i]);
if(f1==f2)return;
if(sum[f1]+sum[f2]>=s[i]){
q.push(i);
}else{
int err=(s[i]-sum[f1]-sum[f2]+1)/2;// 折半,+1是为向上取整
pq[f1].push({err+sum[f1],i});
pq[f2].push({err+sum[f2],i});
}
};
rep(i,1,m){
cin>>a[i]>>b[i]>>s[i];
update(i);
}
while(q.size()){
auto x=q.top();q.pop();
int f1=find(a[x]),f2=find(b[x]);
if(f1==f2)continue;
cout<<x<<' ';
// 启发式合并的基本思想:将小堆合并到大堆,这里令f1是小堆
if(pq[f1].size()>pq[f2].size())swap(f1,f2);
hb(f1,f2);
while(pq[f1].size()){
pq[f2].push(pq[f1].top());
pq[f1].pop();
}
while(pq[f2].size()&&sum[f2]>=pq[f2].top().fi){
update(pq[f2].top().se);
pq[f2].pop();
}
}
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0);
solve();
}
爱提问题的导师
我们已知任意的一个单词的相似度为d(x),
而d(x)表示为单词与目标字符串中最长的相同子串长度,
所以可以看出,本题要求的是最长公共子串的长度,由于数据范围大小的原因,推荐使用二分+哈希串的方式来解决本题,当然可能也有一些其他的奇奇怪怪的解法
将每个单词计算各自的哈希值,接着计算目标字符串的哈希值,
而接下来,就利用二分的方式,暴力的从mid走到单词的结尾,
并且记录到map里,接着计算目标字符串的哈希值是否出现在二分单词内,
接着计算最长长度即可。
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <unordered_map>
using namespace std;
//===========================================
const int MAXN = 1e5+5;
int a[MAXN];
typedef unsigned long long ull;
const int N = 1e5 + 5;
const ull seed = 131;
ull hash1[N][10];
ull hash2[N];
ull p[N];
char s1[N], s2[N];
char str[N];
char seps[] = ",/.-";
string res[N];
int cnt = 0;
int maxlenth = 0;
vector<string> ans;
void hash_val(string s, ull* hash)
{
for (int i = 1; i <= s.size(); i++)
{
hash[i] = hash[i - 1] * seed + (s[i - 1] - 'a' + 1);
}
}
ull get_hash(int w, int len, ull* hash)
{
return hash[w + len - 1] - hash[w - 1] * p[len];
}
bool check(int mid, int lena, int lenb, int id)
{
unordered_map<ull, int>dis;
for (int i = mid; i <= lena; i++)
{
dis[get_hash(i - mid + 1, mid, hash1[id])] ++;
}
for (int i = mid; i <= lenb; i++)
{
if (dis.count(get_hash(i-mid+1, mid, hash2))) return true;
}
return false;
}
void solve()
{
p[0] = 1;
for (int i = 1; i < N; i++)
{
p[i] = p[i - 1] * seed;
}
scanf("%s%s", s1, s2);
char *token = strtok(s1, seps);
while (token != NULL)
{
res[++cnt] = token;
token = strtok(NULL, seps);
}
for (int i = 1; i <= cnt; i ++)
{
hash_val(res[i], hash1[i]);
}
hash_val(s2, hash2);
int lenb = strlen(s2);
for (int i = 1; i <= cnt; i ++)
{
int lena = res[i].size();
int l = 0, r = min(lena, lenb) + 1;
while (l + 1 < r)
{
int mid = l + r >> 1;
if (check(mid, lena, lenb, i)) l = mid;
else r = mid;
}
if (l > maxlenth)
{
maxlenth = l;
ans.clear();
ans.push_back(res[i]);
}
else if (l == maxlenth)
{
ans.push_back(res[i]);
}
}
if (!maxlenth)
{
cout << "None" << endl;
}
else
{
cout << ans.size() << endl;
for (int i = 0; i < ans.size(); i ++)
{
cout << ans[i] << endl;
}
}
}
signed main(signed argc, char const *argv[])
{
#ifdef LOCAL
freopen("in.in", "r", stdin);
freopen("out.out", "w", stdout);
#endif
ios::sync_with_stdio(false);
//===========================================
int T = 1;
while (T --)
{
solve();
}
//===========================================
return 0;
}