多项式时间的验证
对语言的“验证”算法:
- 验证与求解花费时间一样长:最短路径问题的一个实例的证书很容易能在多项式时间内被验证。实际上最短路径问题本身可以在多项式时间内求解。因此,根据指定的证书来验证与从头开始求解这个问题的时间是一样长的。
- 验证可在多项式时间内验证,但是没有多项式时间的判定算法:哈密顿回路问题。
哈密顿回路
哈密顿贿赂问题指的是在无向图 G ( V , E ) G(V,E) G(V,E)中寻找一条通过V中每个顶点的简单回路。具有这种回路的图称为哈密顿图,否则称为非哈密顿回路图。
哈密顿回路问题:“图G中是否具有一条哈密顿回路?”
H
A
M
−
C
Y
C
L
E
=
{
<
G
>
∣
G
是哈密顿回路图
}
HAM-CYCLE=\{<G>|G是哈密顿回路图\}
HAM−CYCLE={<G>∣G是哈密顿回路图}
如何使用一种算法去判定语言HAM-CYCLE。给定一个问题实例,一种判定的算法就是罗列出G的顶点的所有排列,然后对每种排列进行检查,以确定它是否是汉密顿回路。该算法的时间复杂度是阶乘级别的,而不是多项式时间的。
实际上,哈密顿回路问题是NP完全问题。
验证算法
假如提供了一个图,声称该图为哈密顿图,并且给出了一个回路的顶点排列,那么这个问题就变得很容易验证的了:只需要判断这个顶点排列是不是V中的顶点排列,且是否有有连续的边。
我们定义验证算法为包含两个自变量的算法A:
- 其中一个自变量是普通输入串 x x x
- 另一个称为“证书”的二进制串 y y y。
如果存在一个证书
y
y
y满足
A
(
x
,
y
)
=
1
A(x,y)=1
A(x,y)=1,则该含两个自变量的算法A验证了输入串
x
x
x。由一个验证算法A所验证的语言是:
L
=
{
x
∈
{
0
,
1
}
∗
:
存在
y
∈
{
0
,
1
}
∗
,满足
A
(
x
,
y
)
=
1
}
L=\{x\in\{0,1\}^*:存在y\in\{0,1\}^*,满足A(x,y)=1\}
L={x∈{0,1}∗:存在y∈{0,1}∗,满足A(x,y)=1}
如果对任意串
x
∈
L
x\in L
x∈L,都存在一个证书
y
y
y,且算法可以用
y
y
y来证明
x
∈
L
x\in L
x∈L,则算法A就验证了语言L。此外,对任意串$x\notin L
,必然不存在一个能证明
,必然不存在一个能证明
,必然不存在一个能证明x\in L$的证书。
复杂类NP
NP定义
复杂类P是能被一个多项式时间算法验证的语言类。具体地:一个语言L属于NP,当且仅当存在一个两输入的多项式时间算法A和常数c,满足:
L
=
{
x
∈
{
0
,
1
}
∗
:
存在一个证书
y
,
∣
y
∣
=
O
(
∣
x
∣
c
)
,满足
A
(
x
,
y
)
=
1
}
L=\{x\in \{0,1\}^*:存在一个证书y,|y|=O(|x|^c),满足A(x,y)=1\}
L={x∈{0,1}∗:存在一个证书y,∣y∣=O(∣x∣c),满足A(x,y)=1}
我们说算法A在多项式时间内验证了语言L。
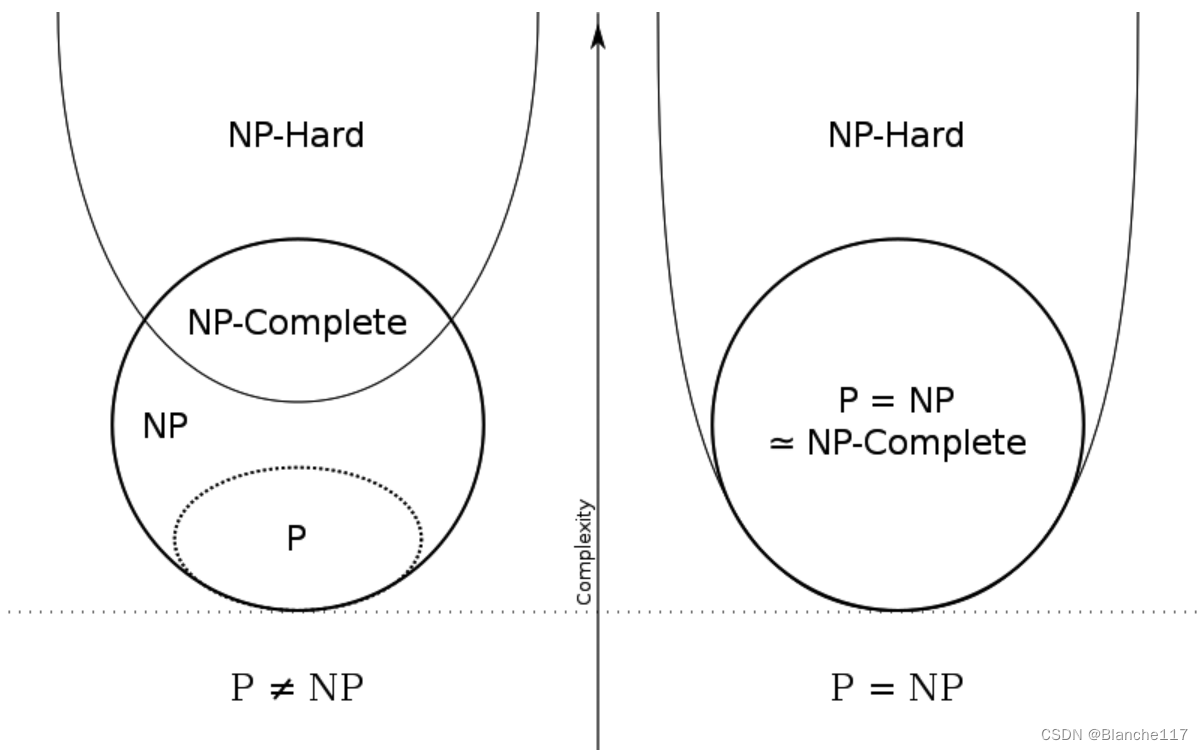
P与NP的关系
基于上述说明,易知, H A M − C Y C L E ∈ N P HAM-CYCLE\in NP HAM−CYCLE∈NP。此外,如果 L ∈ P L\in P L∈P,那么 L ∈ N P L\in NP L∈NP,故 P ⊆ N P P\subseteq NP P⊆NP。
目前还不知道是否有 P = N P P=NP P=NP。从直觉上看,P由一类可以快速被解决的问题组成,而NP由一些可以快速被验证的问题组成。有一些虽然不具备结论性,但是却更令人信服的证据能说明 P ≠ N P P\neq NP P=NP,即存在着“NP完全”语言。
NP完全性与可归约性
NP完全问题特性:如果任何一个NP完全问题能在多项式时间内的到求解,那么,NP中的每一个问题都存在一个多项式时间内的解。
语言HAM-CYCLE是一个NP完全问题,如果我们能在多项式时间内判定HAM-CYCLE,就能在多项式时间内求解NP的每一个问题。事实上,如果能够证明NP-P为非空集,那么可以肯定的是 H A M − C Y C L E ∈ N P − P HAM-CYCLE\in NP-P HAM−CYCLE∈NP−P。
在某种意义上来说,NP完全语言是NP中“最难”的语言。本节我们将使用规约的概念,来说明问题间的难度。
可归约性
可归约性指的是一个问题Q可以被规约为另一个问题Q’。可被规约指的是:
- Q的任何实例都能在多项式时间内转换为Q’的实例
- 且Q’实例的解也是Q实例的解
Q可以被规约成Q’,意味着Q并不比Q’更难解决。
可归约性的形式化语言体系定义为:如果语言 L 1 L_1 L1可以在多项式时间内规约到语言 L 2 L_2 L2,记作 L 1 ≤ p L 2 L_1\leq_p L_2 L1≤pL2,如果存在一个多项式时间可计算的函数 f : { 0 , 1 } ∗ → { 0 , 1 } ∗ f:\{0,1\}^*\rightarrow \{0,1\}^* f:{0,1}∗→{0,1}∗,满足对所有的 x ∈ { 0 , 1 } ∗ x\in\{0,1\}^* x∈{0,1}∗。
规约函数: x ∈ L 1 x\in L_1 x∈L1当且仅当 f ( x ) = L 2 f(x)=L_2 f(x)=L2则称函数 f f f为规约函数
规约算法:计算 f f f的多项式时间算法F称为规约算法
当且仅当,说明了该关系是双向的;即 x ∉ L 1 x\notin L_1 x∈/L1,那么 f ( x ) ∉ L 2 f(x)\notin L_2 f(x)∈/L2

有下面定理:
**定理3:**如果 L , L 2 ⊆ { 0 , 1 } ∗ L_,L_2\subseteq \{0,1\}^* L,L2⊆{0,1}∗是满足 L 1 ≤ p L 2 L_1\leq_p L_2 L1≤pL2的语言,则 L 2 ∈ P L_2\in P L2∈P蕴含着 L 1 ∈ P L_1\in P L1∈P。
NP完全性
多项式时间内规约提供了一种形式方法,用来证明一个问题在一个多项式时间因子内至少与另一个问题一样难。
用小于等于表示可规约可以理解成为难度上的比较
NP完全与NP难度的定义:
语言 L ⊆ { 0 , 1 } ∗ L\subseteq \{0,1\}^* L⊆{0,1}∗是NP完全的,如果
- L ∈ N P L\in NP L∈NP
- 对于每一个 L ′ ∈ N P L'\in NP L′∈NP,都有 L ′ ≤ p L L'\leq_p L L′≤pL
如果一个语言满足性质2,而不一定满足性质1,则称L是NP难度的(NP-hard)的。同时,我们定义NPC为NP完全语言类。
定理4给出了NP完全性是判断P是否等于NP的关键:
**定理4:**如果任何NP完全问题是多项式时间可求解的,那么
P
=
N
P
P=NP
P=NP。等价地,如果存在某一NP中的问题不是多项式时间求解的,则所有NP完全问题都不是多项式时间内可求解的。