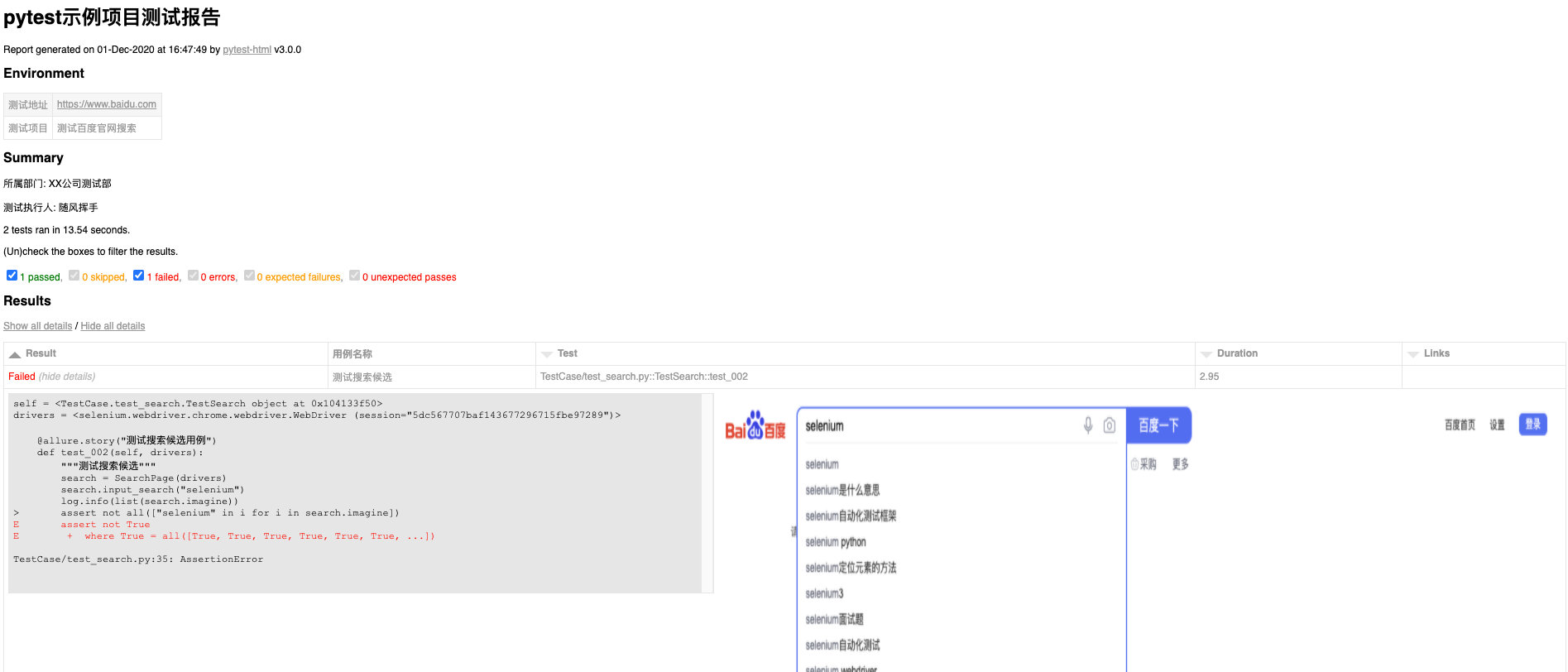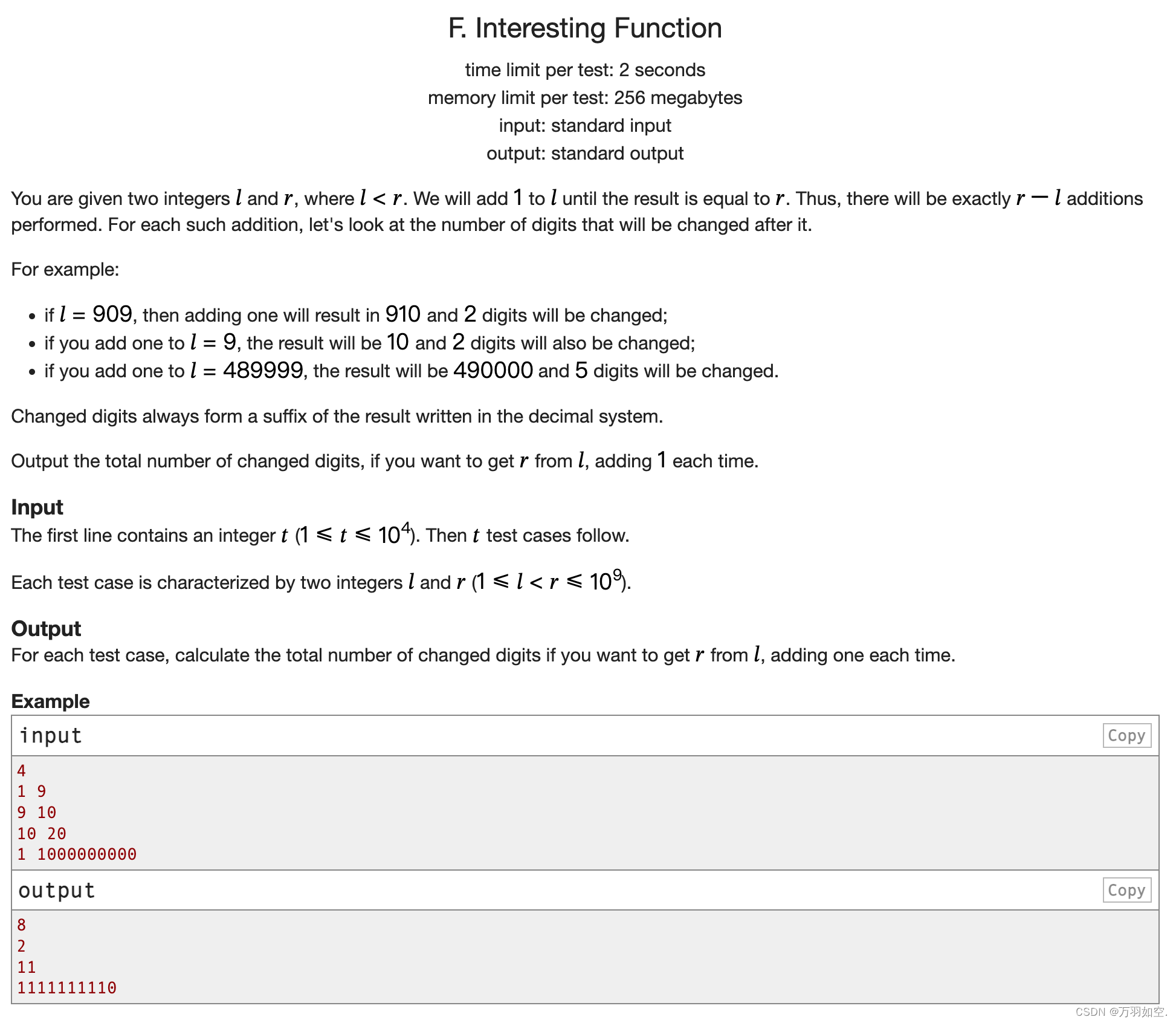
翻译：

给出两个整数𝑙和𝑟，其中𝑙<𝑟。我们将在𝑙上加1，直到结果等于𝑟。因此，执行的添加恰好是𝑟−𝑙。对于每一个这样的加法，让我们看看在它之后将被改变的位数。

例如:

如果𝑙=909，那么增加1将导致910和2位数字将改变;
如果你在𝑙=9上加1，结果将是10,2位数字也会改变;
如果在𝑙=489999中添加1，则结果将是490000，并且将更改5位数字。
更改后的数字总是构成十进制格式的结果的后缀。

如果想从𝑙得到𝑟，则输出更改的数字的总数，每次加1。

输入
第一行包含整数𝑡(1≤𝑡≤104)。然后是𝑡测试用例。

每个测试用例都有两个整数𝑙和𝑟(1≤𝑙<𝑟≤109)。

输出
对于每个测试用例，如果您想从𝑙得到𝑟，计算更改数字的总数，每次增加一个。

例子
inputCopy
4
１ ９
9日10
10个20
1 1000000000
outputCopy
8
2
11
1111111110

思路：

改变的位数，首先我们每次操作，肯定都会改变一次，所以我们可以把初值直接当作r-l，这是个位数的变化，个位数的变化完了，接下来就是十位数，因为个位数的值已经全部拿到，所以没必要记录，我们可以直接/10，把十位当作个位，以此类推，累加就可以得出答案。

代码：

#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <stdio.h>
#include<vector>
#include<queue>
#include<map>
#include<set>
#include<tuple>
#include<numeric>
#include<stack>
using namespace::std;
typedef long long  ll;
int n,t;
inline __int128 read(){
    __int128 x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9'){
        if(ch == '-')
            f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9'){
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}
inline void print(__int128 x){
    if(x < 0){
        putchar('-');
        x = -x;
    }
    if(x > 9)
        print(x / 10);
    putchar(x % 10 + '0');
}

ll m,k;
void solv(){
    cin>>m>>k;
    ll ans=k-m;
    for (int i =10; i<=1e9; i*=10) {
        ans+=k/i-m/i;
    }
    printf("%lld\n",ans);
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(); cout.tie();
    cin>>t;
    while (t--) {
        solv();
    }
    return 0;
}