---

摘要

This week, I read a computer science about time series prediction. This paper firstly applies the recurrent neural network to a new field, namely recommendation system. In real life, the recommendation system can only recommend short-term data. For this problem, the two usual approaches no longer apply, and you should consider modeling the entire session to solve the problem and provide more accurate recommendations to the user. Based on the above information, this paper applies the recurrent neural network to the recommendation system, aiming at solving the problem that recommendation can only be made based on short-term information. Considering the actual situation, the paper makes some modifications to the variation GRUs of recurrent neural network, mainly reflected in the ranking loss function, so as to make the model more suitable for such problems. Finally, the model is compared with the best baseline item-KNN on the two data sets, and the results show that the neural network model is significantly superior to the item-KNN baseline, and the GRU model is improved, making the experimental results excellent. In addition, I learn the following: 1) Analytic Hierarchy Process (AHP) and principal component analysis (PCA), realized them through code after understanding the core idea of the algorithm; 2) Metric tensor, through the idea of duality to explain why the metric tensor has a corrective effect; 3) The finite element method (FEM) introduces how to discretize the continuum and deduce the heat conduction equation.

本周，我阅读了一篇与时间序列预测相关的文章。文章首次将循环神经网络应用于一个新领域，即推荐系统。在现实生活中，推荐系统存在着只能对短期数据进行推荐的问题。对于这个问题，常用的两种方法不再适用，而应该考虑对整个会话进行建模，以此来解决问题，给用户提供更加准确的推荐。基于以上信息，文章将循环神经网络应用于推荐系统，旨在解决只能基于短期信息进行推荐的问题。文章考虑了实际情况，对循环神经网络的变体 GRU 进行一些修改，主要体现在排名损失函数上，以此让模型更加适用于此类问题。最后，在两个数据集上，将模型与最佳基线 item-KNN 进行相比，结果表明神经网络模型明显优于 item-KNN 基线，以及对 GRU 模型进行改进，使得实验结果表现优异。此外，我学习了以下内容：1）层次分析法和主成分分析法，理解了算法的核心思想后，通过代码实现它们；2）度规张量，通过对偶的思想去解释为什么度量张量具有修正作用；3）有限元法，介绍了如何对连续体进行离散化，以及对热传导方程进行推导。

---

文献阅读

1.题目

文献链接：SESSION-BASED RECOMMENDATIONS WITH RECURRENT NEURAL NETWORKS

2.现存问题和解决方法

现存问题：现实生活中的推荐系统只能基于用户的短期信息进行推荐，而不能基于用户的长期历史信息。在这种情况下，常用的方法主要为矩阵分解法和基于邻域的方法。对于缺少 user-items 矩阵的情况，矩阵分解法是不准确的。而采用基于邻域的方法一般只会考虑 session 最后一个事件，比如用户最后一次点击，而忽略了前面的信息。

解决方法：对此，通过对整个用户事件进行建模，给用户提供更准确的建议。因此，利用 RNN 变体的特性，如 LSTM 和 GRU 的记忆性，以此优化基于 session 的推荐，并取得了显著的效果。

3.本文贡献及相关工作

本文工作：
1）证明了 RNN 可以用于基于 session 的推荐，并取得显著的效果；
2）不仅解决了对稀疏序列数据建模的问题，还设计出适配于该推荐任务的排名损失函数来训练模型。

本文贡献：
1）首次将循环神经网络应用到推荐系统中，解决了不能基于用户的长期信息进行推荐的问题；
2）以往的推荐系统只考虑到用户的最后一次点击情况，而忽略了过去的点击信息。对此，将 RNN 应用于基于会话的推荐，通过对整个session进行建模，可以提出更为准确的建议。

4.GRU

1）循环神经网络的主要特点在于网络模型的单元中存在内部隐藏状态，RNN 使用以下更新函数更新其隐藏状态 h ：

2）GRU 旨在解决梯度消失问题，而 GRU 模型有专门的可学习机制决定何时更新隐状态以及何时需要重置隐状态：

3）GRU 有两个门，一个是更新门：

4）候选激活函数：

5）一个是重置门：

5.模型

1）网络的输入是 session 的实际状态，输出是 session 中下一个事件的项。
2）网络的核心是 GRU 层，在最后一层和输出之间可以增加额外的前馈层。
3）网络的输出是 item 的预测偏好，即每个 item 成为 session 下一个item的可能性。

5.1 SESSION-PARALLEL MINI-BATCHES

1）RNN 通常使用 sequence mini-batches，即在句子的单词上使用滑动窗口，并将这些窗口片段彼此相邻以形成小批量，但这不符合本次任务。
2）session 的长度可能不同，甚至会比句子的长度还大。其中有些 session 仅包含2个事件，而其他 session 可能包含数百个事件。
3）目标是捕捉一个 session 是如何随着时间的推移而演变的，因此形成小批量是没有意义的。
4）对此，对序列不等长的情况进行序列补长，即做Padding。需要注意的是，当一个 batch 内的 session 结束时，会用这个 batch 以外的 session 去填补，此时模型的参数需要重新设置。

5.2 SAMPLING ON THE OUTPUT

1）由于 item 数量过大，将对正样本和负样本分别采样计算得分及更新权重。
2）文章提到应该按受欢迎程度对项目进行抽样，但没有为每个训练样例生成单独的样本，而是使用 mini-batch 的其他训练样例中的项目作为负例。
3）这种方法的好处是可以通过跳过采样，进一步减少计算时间。代码实现上也不复杂，从而加快矩阵运算。

5.3 RANKING LOSS

推荐系统的核心是基于相关性的项目排名。文章使用了Pairwise ranking，即比较正样本和负样本的得分，并确保正样本的损失要低于负样本。文章使用了两种基于Pairwise ranking的loss function：
1）BPR：矩阵分解法

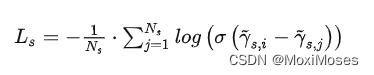
其中：Ns指采样大小，r s,i指desired item的得分，r s,j指负样本的得分。
2）TOP1：正则估计

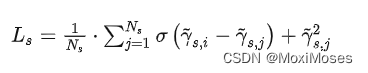
由于正样本会被用于负样本，因此加入正则化项的目的是为了稳定性。

6.实验

6.1 准备

两个数据集：
1）RecSys Challenge 2015，数据集包含电子商务网站的点击流，这些点击流有时以购买事件结束，而使用的训练集只保留点击事件。
2）Youtube-like OTT video service platform Collection，作者自己收集的数据。

验证方式：
1）两个指标，recall@20 和 MRR。
2）通过逐步检查 session 的下一个 event 的 item 排名来进行评估。

6.2 基线

常用的基线：POP、S-POP、Item-KNN、BPR-MF

实验结果表明，item-KNN 方法明显优于其他方法。

6.3 优化

数据集和损失函数的最佳参数化：

实验结果证明了 adagrad 优化效果最好，并且单层 GRU 表现最好。

6.4 结果

Recall@20 和 MRR@20 为不同类型的单层GRU，与最佳基线 item-KNN 进行比较，突出了性能最佳的网络结果：

1）增加GRU的维度可以提升效果；
2）神经网络明显优于 Item-KNN；
3）tanh 作为神经网络输出的激活层更佳；
4）文章设计的 TOP1 loss functio 略优于 BPR。

7.结论

1）作者选择了基于 session 的推荐任务，因为这是一个非常重要的领域，但没有得到很好的研究。
2）作者通过引入 session 并行小批量、基于小批量的输出采样和排序损失函数，对 GRU 模型进行修改，以更好地适应任务。
3）作者认为这项工作可以成为推荐系统中深度学习的应用和基于 session 推荐的基础。
4）作者计划在自动提取的项目表示上训练网络，该表示基于项目本身的内容上，而不是当前的输入。

数学建模

1.综合评价模型的一般步骤

1）明确评价目的；
2）确定被评价对象；
3）建立评价指标体系（包括评价指标的原始值、评价指标的预处理等）；
4）确定与各项评价指标相对应的权重系数；
5）选择或构造综合评价模型；
6）计算各系统的综合评价值，并给出综合评价结果。

参考链接：https://zhuanlan.zhihu.com/p/109925628

2.层次分析法

python实现层次分析法：

import numpy as np


# 层次分析法
class AHP:

    # 准备相关信息
    def __init__(self, array):
        # 记录矩阵相关信息
        self.array = array
        # 矩阵大小
        self.n = array.shape[0]
        # 初始化RI值, 用于一致性检验
        self.RI_list = [0, 0, 0.52, 0.89, 1.12, 1.26, 1.36, 1.41, 1.46, 1.49, 1.52, 1.54, 1.56, 1.58,
                        1.59]
        # 矩阵的特征值和特征向量
        self.eig_val, self.eig_vector = np.linalg.eig(self.array)
        # 矩阵的最大特征值
        self.max_eig_val = np.max(self.eig_val)
        # 矩阵最大特征值对应的特征向量
        self.max_eig_vector = self.eig_vector[:, np.argmax(self.eig_val)].real
        # 矩阵的一致性指标CI
        self.CI_val = (self.max_eig_val - self.n) / (self.n - 1)
        # 矩阵的一致性比例CR
        self.CR_val = self.CI_val / (self.RI_list[self.n - 1])

    # 一致性判断
    def test_consist(self):
        # 一致性指标CI和一致性比例CR
        print("判断矩阵的CI值为：" + str(self.CI_val))
        print("判断矩阵的CR值为：" + str(self.CR_val))
        # 一致性检验判断
        if self.n == 2:
            print("仅包含两个子因素，不存在一致性问题")
        else:
            if self.CR_val < 0.1:
                print("判断矩阵的CR值为" + str(self.CR_val) + ",通过一致性检验")
                return True
            else:
                print("判断矩阵的CR值为" + str(self.CR_val) + "未通过一致性检验")
                return False

    # 算术平均法求权重
    def cal_weight_by_arithmetic_method(self):
        # 矩阵的每列的和
        col_sum = np.sum(self.array, axis=0)
        # 判断矩阵按列进行归一化
        array_normed = self.array / col_sum
        # 计算权重向量
        array_weight = np.sum(array_normed, axis=1) / self.n
        print("算术平均法计算得到的权重向量为：\n", array_weight)

        return array_weight

    # 几何平均法求权重
    def cal_weight__by_geometric_method(self):
        # 矩阵的每列的积
        col_product = np.product(self.array, axis=0)
        # 将得到的积向量的每个分量开n次方
        array_power = np.power(col_product, 1 / self.n)
        # 将列向量归一化
        array_weight = array_power / np.sum(array_power, axis=0)
        print("几何平均法计算得到的权重向量为：\n", array_weight)

        return array_weight

    # 特征值法求权重
    def cal_weight__by_eigenvalue_method(self):
        # 将矩阵最大特征值对应的特征向量进行归一化处理
        array_weight = self.max_eig_vector / np.sum(self.max_eig_vector)
        print("特征值法计算得到的权重向量为：\n", array_weight)

        return array_weight


if __name__ == "__main__":

    # 判断矩阵
    b = np.array([[1, 1 / 3, 1 / 8], [3, 1, 1 / 3], [8, 3, 1]])
    
    if AHP(b).test_consist():
    	# 算术平均法求权重
        weight1 = AHP(b).cal_weight_by_arithmetic_method()
        # 几何平均法求权重
        weight2 = AHP(b).cal_weight__by_geometric_method()
        # 特征值法求权重
        weight3 = AHP(b).cal_weight__by_eigenvalue_method()

三种不同方法得到的权重向量：

判断矩阵的CI值为：(0.0007708125321130854+0j)
判断矩阵的CR值为：(0.0014823317925251641+0j)
判断矩阵的CR值为(0.0014823317925251641+0j),通过一致性检验

算术平均法计算得到的权重向量为：
 [0.08199023 0.23644689 0.68156288]
几何平均法计算得到的权重向量为：
 [0.68172455 0.2363407  0.08193475]
特征值法计算得到的权重向量为：
 [0.08193475 0.2363407  0.68172455]

关键点：
1）确立层次结构：将决策问题分解为不同的层次，并建立层次之间的关系。
2）设定因素权重：对于每个层次中的因素，确定其相对重要性，设计一个标准化比较矩阵以计算各因素之间的权重。
3）一致性检验：检查矩阵的一致性，确保标准化比较矩阵具有合理的比例关系。
4）计算成绩：计算每个层次中的因素和决策方案的总成绩。
5）敏感性分析：通过重新计算成绩，确定权重变化对最终结论的影响。

3.主成分分析法

python实现主成分分析法：
1）利用奇异值分解（SVD）来处理线性代数问题；
2）测试数据是一个二维的数据matrix。

import numpy as np


def pca(matrix):

    # 中心化
    mean_matrix = np.mean(matrix, axis=0)
    matrix = matrix - mean_matrix

    # 计算协方差矩阵
    covariance_matrix = np.cov(matrix, rowvar=False)

    # 奇异值分解
    U, S, V = np.linalg.svd(covariance_matrix)

    # 将数据映射到新的空间中
    new_matrix = np.dot(matrix, U)

    # 计算权重
    weights = np.abs(V[0])

    return new_matrix, weights


# 测试代码
data = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])
print(data)

new_matrix, weights = pca(data)
print("new_matrix:")
print(new_matrix)
print("weights:")
print(weights)

计算得到权重向量：

[[1 2]
 [2 3]
 [3 4]
 [4 5]]
 
new_matrix:
[[ 2.12132034e+00 -2.22044605e-16]
 [ 7.07106781e-01 -5.55111512e-17]
 [-7.07106781e-01  5.55111512e-17]
 [-2.12132034e+00  2.22044605e-16]]
weights:
[0.70710678 0.70710678]

python实现PCA降维：

import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris


# 准备数据集
data = load_iris()
y = data.target
x = data.dataa

# PCA算法，设置降维后主成分数目为2
pca = PCA(n_components=2)
reduced_x = pca.fit_transform(x)

red_x, red_y = [], []
blue_x, blue_y = [], []
green_x, green_y = [], []

for i in range(len(reduced_x)):
    if y[i] == 0:
        red_x.append(reduced_x[i][0])
        red_y.append(reduced_x[i][1])

    elif y[i] == 1:
        blue_x.append(reduced_x[i][0])
        blue_y.append(reduced_x[i][1])

    else:
        green_x.append(reduced_x[i][0])
        green_y.append(reduced_x[i][1])

# 进行可视化
plt.scatter(red_x, red_y, c='r', marker='x')
plt.scatter(blue_x, blue_y, c='b', marker='D')
plt.scatter(green_x, green_y, c='g', marker='.')
plt.show()

可视化结果：

数学推导参考链接：https://blog.csdn.net/huangguohui_123/article/details/105574175

度规张量

1.度量张量的本质

为什么度量张量有修正作用？其实不是度量张量有修正作用，而是任何坐标系下的向量表达式都可以变换成特定坐标系的同一个形式。因此，度量张量的本质就是向量在任意坐标系的读数对自己点乘的算式结果中的基向量的那一部分。

在某个坐标系中，P = x dot g1 + y dot g2，在另外一个坐标系中，P = x’ dot g1’ + y’ dot g2’，如果有 g1’ = a dot g1 + b dot g2，g2’ = c dot g1 + d dot g2，则我们可以把g1’，g2’ 用 g1，g2 表示。将其代入到 P = x’ dot g1’ + y’ dot g2’，一定可以得到 P = x dot g1 + y dot g2。

有了对偶坐标系和原坐标系之间的转换关系，就以对偶坐标系举例说明。上周学到向量内积可以被理解为矩形面积，那么在任意坐标系下，长度可以用向量与自己做内积开平方来定义（正方形面积）。

由此可知，我们只需要证明以下等式即可：

2.为什么可以用 gi dot g^i 的形式来定义度量张量

从对偶坐标系之间读数转换的角度来理解度量张量，坐标变换需要一个坐标变换矩阵。而坐标变换矩阵，按线性代数中坐标变换的法则，就是一个坐标系的两个基向量在其对偶坐标系的读数，即 g1 = a dot g1’ + b dot g2’，g2 = c dot g1’ + d dot g2’，这个也可以写成矩阵形式。

在前面的学习中，我们知道向量 P 与当前基向量 gi 的点乘，就是 P 在对偶坐标系中的读数。于是，一个基向量在它的对偶坐标系的读数，只要将它与基向量点乘就可以得到。

因此，求 g1 在其对偶坐标系 g^1, g^2 中的读数，即 g1 = a dot g1’ + b dot g2’，只需要将 g1 与 g1, g2 分别点乘，再将这个作为矩阵 G 的第一列。同理可得，度量张量的形式：

其中：a = g1 dot g1，b = g1 dot g2，由点乘的定义可知，矩阵沿对角线对称。

3.为什么度量张量等于 CT dot C

C表示两个基矢量在某个坐标系中的读数构成的矩阵，g1x 等读数可以是针对任意坐标系的，是基矢量 gi 在那个坐标系中的读数：

基矢量点乘来定义度量张量，需要把基矢量做个转置：

写成矩阵形式，左边的矩阵每一行是一个基向量，右边的矩阵每一列是一个基向量：

4.自然基矢量和协变基矢量

在极坐标系中，从极坐标系到直角坐标系有一个全局的变换关系，定义为：
需要注意的是，大部分坐标系是局部的，不是所有到直角坐标系的变换关系都是一样的，甚至都不一定有函数式的变换关系。

在极坐标系中任意一点 r0, θ0处，可以建立一个局部坐标系。基向量分别为：

其中：这两个向量就是这个局部坐标系的协变基矢量，而逆变基矢量则是这对协变基矢量的对偶基向量。这两个基向量的原点是 x0 = r0 cosθ0，y0 = r0 sinθ0。

有限元法

1.介绍

1）有限元法可以将连续的实体域离散成一个个的单元，将每个单元都描述清楚，然后再通过某种规则组合起来。因此，遇到问题不要慌，离散化处理，从小到大，从易到难。

2）现在，怎么描述单个单元呢？如下图所示：

这是一个四面体单元，有6条边和10个黑点，但不都是顶点，这10个点就是所谓的单元节点（nodes）。因此，这10个节点在空间中的位移就决定了四面体的任意变形，四面体内部区域任意点的位移也可以通过简单的多项式函数（基函数）对10个节点进行插值得到。这里只介绍了点的位移坐标，同样地，对于其他参数如温度、应力等，也可以通过同样的方法得到。

2.热传导基本原理

其实大部分控制方程就是守恒方程，而质量守恒、能量守恒、动量守恒就是保证一个系统的物理量不会凭空消失也不会凭空产生，即控制方程就是控制该系统物理量的各种变化需要满足上面的要求。而这种方程的推导往往会任取一个控制体（微元），如下图一个用于传热问题的控制体：

假设上面控制体里的能量密度为 u，即每单位体积所含热能 J，单位：J/m3，那么控制体里的总热能 U（单位J，焦耳）等于（记为公式1）：

这个量由两部分组成：
1）自身产热 +
假设自身产热是 Q，每单位体积和单位时间下的产热，单位：J/(s * m3)，那么总产热可以积分得到（单位时间，记为公式2）：

2）流进/流出 +/-
流进流出都是通过控制体表面实现的，因此定义一个物理量，即有方向的热流密度/热通量 q（矢量），意义是单位面积单位时间所通过的热量，单位为：J/(s * m3)，那么流进流出就可以用一个公式来表明，不管是流进还是流出，可以用热流密度的符号来区分，那么流进流出的热能可以积分得到（单位时间，记为公式3）：

其中：n 是 q 所在面 S 的法向方向，对于一个封闭体，边界面的法向方向都朝外，因此 q 与 n 方向相同则流出，q 与 n 方向相反则流进。于是，我们可以来描述守恒方程，前面的公式2和公式3描述的是单位时间的热能变化，单位为：J/s。因此，需要公式1对时间求导，这样就包含了时间的变化，即瞬态情况：

3.进一步推导

1）Cv 指定容比热，是固体材料的特征性质；
2）散度定理把面积分变为体积分，从而把积分符号取掉；
3）公式10 是局部平衡方程，与流体力学类似，既有积分表示，又有微分表示控制方程；
4）在傅里叶导热定理中，(grad T)‘表示grad T的转置，k表示热导率；
5）我们一般遇到热各向同性材料，进一步来说，梯度的散度就是拉普拉斯算子。

---

总结

本周，我学习了有限元法，有限元法的核心思想是通过将连续体离散化，以小见大，从局部到整体，由单元组合成整体域，化繁为简，研究单个单元来得到普遍的规律。说起来简单，但是会遇到如何离散化？无数个单元都需要单独描述？有限元还涉及到那么多的面积分、体积分？之类的问题，本周学习了离散化和热传导基本原理，以及热传导方程的推导，下周将会学习如何求解这个方程，当然求解偏微分方程需要边界条件，因此需要去了解边界条件。