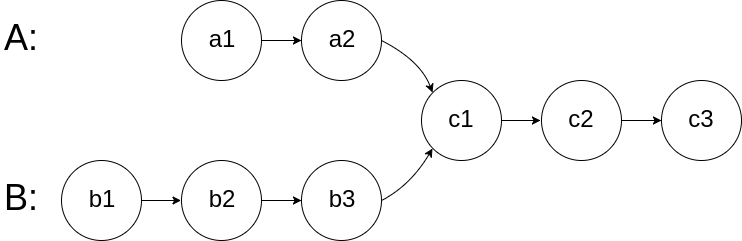
说在开头：关于海森堡的矩阵（2）

海森堡写完论文就回到了哥廷根大学，他一看见玻恩就把这份论文拿出来请老师把关，还说要趁着假期去趟英国剑桥大学讲课交流。玻恩拿过论文一看，海森堡画的这个表格是啥玩意啊？怎么乘法交换律都失效了，不过这东西好面熟，怎么这么像当年学的矩阵呢？玻恩恍然大悟，原来这小子自己又重新发明了一遍矩阵。玻恩快速地看完这篇论文，海森堡最后推算的结果真是让人激动不已：过去旧量子论中电子圆轨道的那些毛病全都没有了。不过此时他需要找个人帮忙，用矩阵的标准写法把海森堡的东西重新整理一遍，心里想：诶，那个大师兄泡利应该可以啊。结果泡利一听这想法说：你看看你就喜欢这种复杂冗长的数学形式，搞那么复杂干啥哪？这样只会损害海森堡的物理思想。说完后怎么都不肯干了。泡利因为他那火力全开的暴脾气，经常跟伟大的发现失之交臂，前一阵子刚搞的那个美国人错过了“量子自旋”，差点买了块豆腐一头撞死，这回自己又错过了伟大的量子物理学里程碑。

玻恩也拿泡利没办法，这小子不好惹啊，那找谁干呢？这时有个助手冒了出来找玻恩，表示自己可以试试看。这个话都说不利索的小伙子就是他的助手约旦，由于口吃他平常不大爱说话。于是两个人开始整理海森堡的论文，完全转化成标准的矩阵写法。不要再叫“格子”来“格子”去的了，传出去又让隔壁的老头子希尔伯特笑话物理学家没文化了。这篇论文写的很详细，首先要科普一下什么是矩阵，然后切入正题进入海森堡的矩阵力学，还要特别强调：A x B ≠ B x A。有了正统的矩阵工具，海森堡的矩阵理论立刻大发神威，计算出来是跟经典力学兼容的，举个栗子：能量守恒等；而不像玻尔前阵子搞的那啥BKS理论，非要跟能量守恒过不去。玻恩和约旦就发表了这篇论文，史称“两个人的文章”。

海森堡那时还在英国剑桥讲学（游玩），那时有一个苏联学生去剑桥访问，据说经费还是列宁特批的；由于当时双方的意识形态处于敌对状态，苏联跟西欧国家关系不好，德国、法国、荷兰都不肯收这帮苏联学生，他们这才来到了英国，卢瑟福倒是非常欢迎。有个学生想留下来读研究生，其实他在苏联国内已经当上讲师了，这个小伙子就是卡皮查，后来他和朗道成为了苏联物理学界的顶梁柱，也是研究低温的开创者。海森堡在英国讲学的时候对自己的“格子”还没有信心，所以在讲课时就没提这事，当时卡皮查组织了一个俱乐部，就是晚上一伙人聚聚会，大家无拘无束，海森堡就在卡皮查的俱乐部上把自己的成果讲了出来：我发明了一种好玩的“格子”算法，几个表格来回一搞就能算出原子光谱。参加聚会的有个人叫富勒，他对这“格子”很感兴趣，就问海森堡能不能把论文寄给他一份，海森堡当然很乐意。海森堡讲学完后就回家跟玻恩、约旦三个人合伙写了一篇论文，讲述了如何把海森堡的矩阵力学从一个自由度扩展到所有自由度上。这篇文章史称“三个人的文章”。

富勒后来拿到了海森堡的论文，他给了他的学生一份副本。这个学生也是卡皮查俱乐部成员，但当天有事没去，所以没听到海森堡讲“格子”；他原本是搞相对论研究的，在老师富勒的影响下对原子光谱特感兴趣，玻尔大师到剑桥讲学时他一听就入迷了。这小伙叫狄拉克，1902年出生，比海森堡还小了一岁。狄拉克看到海森堡论文，一眼就看到问题的关键：这“格子”不满足乘法交换律啊。他隐约记得好像哪里看到过类似的东西，于是等过了周末去图书馆一通找（周末图书馆不上班），终于找到了他需要的东西：泊松括号（对，就是“泊松亮斑”的那位法国大数学家泊松）。狄拉克发现，假如海森堡的“格子”用泊松括号的形式改写一下，就会变得清晰简洁，而且还符合乘法交换律。狄拉克方程的好处是：不需要引进物理学家普遍头疼的矩阵，在原来经典力学的基础上打个布丁，就解决了问题。于是他写了一封信给海森堡，海森堡一看：这东西好是好，就是晚了一步，他已经跟玻恩老师和小师弟约旦搞出矩阵力学的论文了。狄拉克又去完整地计算了一下氢原子的光谱线，看看是不是跟实验观测完全吻合；结果又晚了一步，泡利抢在他之前用矩阵力学计算了一遍，吻合得很好。

矩阵力学的论文当年在大多数物理学家那里反响平平，因为大家都还不懂矩阵是啥，更不用说矩阵力学了，大家都被整的一头雾水，还是先恶补下矩阵吧。（参考自：吴京平-无中生有的世界）

二，升压型（BOOST）拓扑

大家知道开关电源的基本拓扑有且只有三种：降压型（BCUK），升压型（BOOST），升降压型（BUCK-BOOST）；从中文命名中我就可以知道降压型拓扑只负责降压，该特性上类似于线性电源变换器（LDO），但升压型拓扑，顾名思义，就是只负责电源升压变换的拓扑。降压比较容易理解，那升压是怎么实现的呢？

1，升压型（BOOST）拓扑原理

如下图所示为升压型（BOOST）电源拓扑的结构示意图，其结构与BUCK电路的主要不同在于：在Vdc和开关Q1之间串接了一个电感器L1，电感器L1的右端通过整流二极管D1（非续流二极管）给输出电容C0及负载供电。

1. Q1导通时：电流方向为Vdc通过L1和Q1到GND，而负载电流（Io）全部由输出电容器C0提供；所以C0应足够大，以使在Ton时间段内向负载供电时的输出电源电压降满足设计要求；

——Q1导通时电流路径为：从Vdc流到了GND，并没有能量传输到输出端；感觉这不是浪费电能了么？其实理想情况下（不考虑电感器DCR和MOS管导通电阻，P = I²*R = 0）并不会损耗电能，而是将能量储存到了电感器L1中。

2. Q1关断时：由于电感器电流不能突变，电流方向为Vdc通过L1和D1向C0和负载供电，此时C0两端电压高于Vdc；此时Vdc电源和电感器储能（总共两部分）给负载和C0供电（补充电容器C0单独向负载供电时（ton阶段）损失的静电场能）；

——Q1关断，经过电感器L1的电流由增加变成减小（电流变化率产生变化），所以电感器的感应电压方向发生转变，即由原来的左高右低（与Vdc抵消）变成左低右高（与Vdc叠加），此时输出电压Vo会高于Vdc。

3. 输入电容器串联电感器，所以输入电容电流是“平滑”的，如下左图所示；

4. 输出电容器串联的是二极管（D1），所以输出电容器的电流是斩波式的，如上右图红色线所示，必然会影响输出电源的波动；

——BOOST拓扑的输出电源纹波电流相对BUCK拓扑来说更大，所以对BOOST拓扑的输出电容器有更高的要求：ESR更低、容量更大等。

5. 对于输出电容来说，在稳态下其平均电流为0（同BUCK拓扑），那么BOOST拓扑的平均二极管电流必然等于负载电流，所以Id_avg = Io=IL*(1-D)，IL= Io/(1-D)，这是平均电感器电流和负载电流的关系。

6. 输出电压的调整是通过反馈环路控制Q1的导通时间Ton来实现的，若直流负载电流Io上升，则导通时间Ton会自动增加为负载提供更多的能量。

同样，根据BOOST拓扑也可以通过伏秒定律来推导直流传递函数：Von = Vin – Vsw，Voff = Vo + Vd – Vin，Von*Ton = Voff * Toff，那么1/D = T/Ton = (Toff+Ton)/Ton = (Vo+Vd-Vsw)/(Vo+Vd-Vin)，所以D = (Vo+Vd-Vin)/ (Vo+Vd-Vsw)，如果MOS管压降（Vsw）和二极管压降（Vd）相比输入/输出电源电压都很小，那么D ≈ (Vo-Vin)/Vo，输出与输入之间的关系为：Vo = Vin* [1/(1-D)]。

Boost开关电源同样有两个工作模式：连续工作模式和不连续工作模式；如下图所示。

1. 不连续工作模式：如上左图所示，若Q1在下次导通之前，流过D1的电流已下降为0，则认为上次Q1导通时存储于L1的能量已释放完毕（磁芯复位），电源电路工作于不连续模式；

2. 连续工作模式：如上右图所示，若电流在Q1关断时间结束时流过D1的电流还未下降到0，由于电感器电流不能突变，Q1下次导通时电流会产生一个台阶：Q1和D1上的电流将呈典型的阶梯斜坡形状；

——其本质同上一章节举例的BUCK开关电源的连续导通模式和断续导通模式是一样的，与电源输出负载电流的大小有关。

3. 若反馈环在不连续工作模式正常工作，当R0或Vdc减小时，反馈环路会增加Ton以保持输出电压恒定；若R0或Vdc继续减小，则可能使Ton增大到下次导通之前D1电流仍未降到0，此时电路进入连续工作模式；

4. 能使不连续工作模式下反馈环稳定工作的误差放大电路，不能使连续工作模式下的反馈环稳定，并会产生振荡。

——如上一章“开关调整器的不同工作模式”所述，连续导通模式和断续导通模式的反馈环路设计是不一样。

2，不连续模式下的参数设计

BOOST开关电源工作在不连续模式下，首先需要确保工作模式不会跨越到连续模式，具体步骤如下：

1. D1电流在Q1再次导通时正好降为0，这是不连续工作模式的临界点；

——在临界不连续情况下，Vdc或R0任何微小的减小都会导致电路进入连续工作模式，若误差放大器未针对连续工作模式设计，则会引起振荡（增加Ton，导致D1电流增大）。

2. 为避免出现临界不连续的情况，需要选择恰当的开关导通时间（Ton），以保证在最大导通时间时，D1电流也能降为0，并且与Q1再次导通之间仍留有一定的死区时间：Tdt，如上左图所示；

3. D1电流下降至0时，L1的磁心磁通必然恢复至磁滞回线的起点；磁心不允许在磁滞回线上一直沿单方向磁化，若给定伏秒数（E*dt）从B1点移到B2点，则磁心再次沿磁滞回线磁化上移之前必须施加反极性伏秒数使其精确回到B1点，如上右图所示；

——假如绕组施加同名端为正的电压使磁芯发生正向磁化dB = B1-B2，若磁芯密度从B1变化到B2后，加反压使他复位复位到哪怕只比B1高一点，若干周期后磁芯密度会达到磁滞曲线饱和段使磁芯饱和，从而造成开关管损坏。

4. Q1导通时L1同名端极性为正，磁心伏秒数：Vdc*Ton，驱动沿磁滞回线置位；Q1关断时L1电压极性反向，磁心沿磁滞回线恢复至起点位置，磁心伏秒数：（Vo-Vdc）*Tτ=Vdc*Ton；

5. 为保证电路工作于不连续模式，设定整个周期的20%为死区时间Ttd；这样，最大导通时间+磁心复位时间+死区时间（T = Ton + Tτ +Ttd），构成整个工作周期，保证L1的电流降低到0与Q1再次导通之间有20%周期的间隔；

6. 根据Q1导通和关闭伏秒数相等，Vdc*Ton = （Vo-Vdc）*Tτ， Ton+Tτ=0.8T；可得：Ton= [0.8T*(Vo-Vdc)]/Vo。

三，升降压型（BUCK-BOOST）/反极性拓扑

升降压拓扑实现了开关电源升压和降压两种功能，实际上升降压拓扑是：正输入对负输出的（或负输入对正输出），如下图所示，无论输入极性如何输出都会反向，因此升降压拓扑也被称为反极性拓扑。

1，升降压型拓扑原理

升降压拓扑工作原理：在一个周期（Ton）的一段时间内使电感储能，而在后的一段时间内（Toff）将电感能量传递给负载；拓扑结构示意图及工作状态如下图所示。

1. 正输入负输出的BUCK-BOOST拓扑电路，可以将+12V电压降为-5V或则升压为-15V；或则负输入的-12V电压变换为+5V或则+15V，输出电压可以大于、等于或则小于输入电压（电压幅值）；

2. Q1导通时：电流方向为Vdc通过Q1和L0到GND，将Vdc输入能量储存在L0中，此时负载电流（Io）全部由输出电容器C0提供；所以C0应足够大，以使在Ton时间段内向负载供电时的输出电源电压降满足设计要求；

3. Q1关断时：由于电感器电流不能突变，电流方向为Vo通过D1和L0到GND，给C0反向充电，此时C0两端电压极性为上负下正（负压）；此时输入已断开，所有负载所消耗能量和给电容器C0充电的能量全部由电感器L0提供；

——我们看到BUCK-BOOST拓扑中没有输入电源Vdc直接提供能量给输出的路径（BUCK和BOOST拓扑中都有），即只有反激式拓扑（包括BUCK-BOOST）所有的能量都必须先储存在电感器中，对电感器要求更高：若Q1导通时存储于L0的电流Ip在Q1再次导通之前下降到0（工作于不连续模式），那么提供给负载的功率为：Pt =1/2*L0*I²p/T。

4. 输入电容器串联开关（MOS管），所以输入电容的电流是“斩波式”的，如下左图所示；

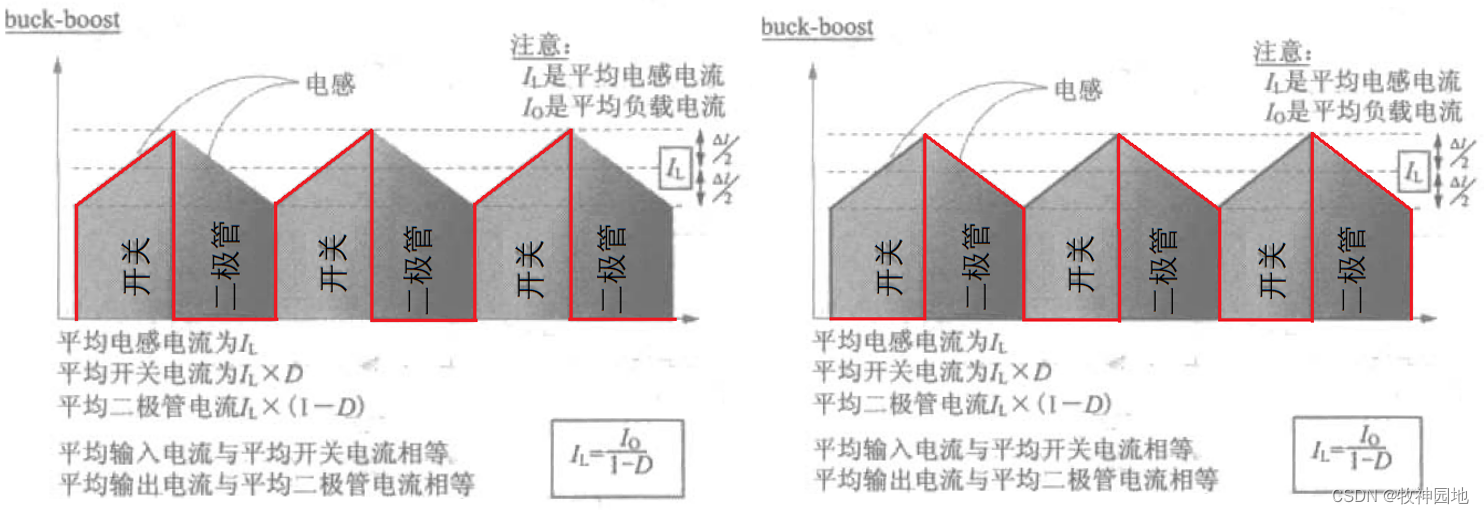
5. 输出电容器串联的是二极管（D1），所以输出电容器的电流也是斩波式的，如上右图红色线所示，必然会影响输出电源的波动；

6. 发热损耗与电流IRMS值成比例，脉冲电流的RMS值很大，降低了BUCK-BOOST拓扑电路的效率，同时输入/输出电源的PCB上会有很大噪声和纹波；

——BUCK-BOOST拓扑的输入/输出电源纹波电流都很大，所以对BUCK-BOOST拓扑来说的输入/输出电容器的要求都很高：低ESR、大容量等。

7. 对于输出电容来说，在稳态下其平均电流为0（事实上任何电源拓扑的稳态平均电流都为0），那么BUCK-BOOST拓扑的平均二极管电流必然等于负载电流，所以Id_avg = Io=IL*(1-D)，IL= Io/(1-D)，这是平均电感器电流和负载电流的关系（同BOOST拓扑一样）；

8. 输出电压的调整是通过反馈环路控制Q1的导通时间Ton来实现的，若直流负载电流Io上升，则导通时间Ton会自动增加为负载提供更多的能量。

根据BUCK-BOOST拓扑也可以通过伏秒定律来推导直流传递函数：Von = Vin – Vsw，Voff = -Vo + Vd，Von*Ton = Voff * Toff，那么1/D=T/Ton = (Toff+Ton)/Ton = (Vin-Vsw+Vd-Vo)/(-Vo+Vd)，所以D =  (-Vo+Vd)/ (Vin-Vsw+Vd-Vo)，如果MOS管压降（Vsw）和二极管压降（Vd）相比输入/输出电源电压都很小，那么D ≈ (-Vo)/[Vin+(-Vo)]，输出与输入之间的关系为：(-Vo) = Vin* D/(1-D)。

2，不连续模式下的参数设计

BUCK-BOOST电源拓扑同Boost拓扑一样，需保证导通时间最大时，存储于L0的电流能在Tτ末端下降至0；并距再次导通留有0.2T的死区，以保证其工作于不连续模式；Ton+Tτ=T-Tdt=0.8T。

同BOOST电源拓扑一样，BUCK-BOOST电源拓扑要求导通伏秒数与关断伏秒数相等以防止磁心饱和；所以Vdc*Ton=Vo*Tτ，结合两个公式可得：Ton= 0.8*Vo*T/(Vdc+Vo)；假设输出效率为100%，那么Po= V²o/Ro = Pt = 1/2*L0*I²p/T；由于Ip=Vdc*Ton/L0，可得： Vo=Vdc*Ton*√[Ro/(2T*Lo)]。

在已知Vo、Vdc、Ro和T情况下，结合Ton公式可计算L0值。