选择排序
- 1. 直接选择排序
- 2. 堆排序
- 2.1 堆
- 2.2 堆的实现(以大根堆为例)
- 2.3 堆排序
- 3. 堆排序(topK问题)
1. 直接选择排序
-
思想
以排升序为例。以a[i]为最大值(或最小值),从a[i+1]到a[n-1-i]比较选出最大值放在a[n-1-i](或最小值放在a[i])。简单讲就是将以每轮排序的第一个数作为最大值或者最小值,比较剩余的元素,得到最大值或者最小值,将最大值放在剩余数据的最后一位,最小值放在剩余数据的第一位。
升级版
以排升序为例。每轮排序中选出最大值和最小值,分别放在数据的左右两端。 -
例子(排升序)

-
代码实现
//选择排序(以排升序为例)
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void SelectSort(int* a, int n)
{
int left = 0;
int right = n - 1;
while (left < right)
{
int maxi = left, mini = left;
for (int i = left + 1; i <= right; i++)
{
if (a[i] > a[maxi])
{
maxi = i;
}
if (a[i] < a[mini])
{
mini = i;
}
}
Swap(&a[maxi], &a[right]);
//这里要考虑特殊情况:如果最小值mini==right,那么在交换maxi和right后,
//最小值就发生改变,所以要最小值的下标要改变。
if (mini == right)
{
mini == maxi;
}
Swap(&a[mini], &a[left]);
right--;
left++;
}
}
- 算法分析
时间复杂度
假设有n个元素,第一次排序要遍历n-2个元素,第二次排序要遍历n-4个元素,往后每次排序的元素个数都减2,总的遍历次数是等差数列的前n项和,所以时间复杂度是O(N^2)。
空间复杂度
空间复杂度是O(1)。
稳定性
是不稳定的排序。如上面的例子中的12,在选出最大值和最小值时,前后顺序发生改变。
注意
直接选择排序的最好情况和最坏情况的时间复杂度都是O(N^2)。
2. 堆排序
2.1 堆
-
概念
堆其实是一种树形结构,分为大根堆和小根堆。大根堆是树中所有父节点大于子节点,小根堆是树中所有父节点小于子节点。但父节点的左右孩子谁大谁小没有要求。 -
预备知识
(1)堆的逻辑结构是树,物理结构是数组(即在内存中以数组的形式存储)。
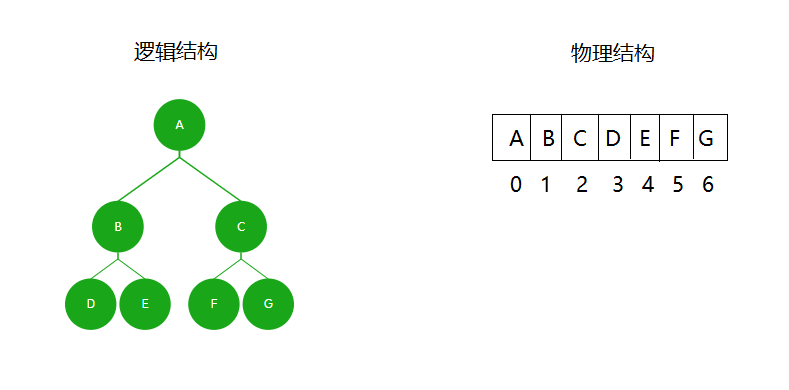
(2)父节点和子节点的关系
已知子节点下标,它的父节点下标parent = (child - 1)/2。
已知父节点下标,它的子节点下标leftchild = parent * 2 + 1,rightchild = parent * 2 + 2。
(3)种存储结构只适用于满二叉树和完全二叉树,否则会浪费很多空间。
2.2 堆的实现(以大根堆为例)
- 堆的定义
//堆的实现
typedef int HPDataType;
typedef struct Heap
{
HPDataType* a;//用来申请空间
int size;//记录当前堆的元素个数
int capacity;//记录当前堆的最大容量
};
- 堆的初始化
//堆的初始化
void HeapInit(HP* ph)
{
assert(ph);
ph->a = (HPDataType*)malloc(sizeof(HPDataType)*10);//初始化容量设置为10
if (ph->a == NULL)
{
perror("malloc failed");
return;
}
ph->capacity = 10;
ph->size = 0;
}
- 入堆
//入堆
void HeapPush(HP* ph, HPDataType x)
{
assert(ph);
//首先要检查堆是否已满
if (ph->size == ph->capacity)
{
HPDataType* tmp = (HPDataType*)realloc(ph->a, sizeof(HPDataType) * ph->capacity * 2);
if (tmp == NULL)
{
perror("realloc failed");
return;
}
ph->a = tmp;
ph->capacity *= 2;//每次容量不够时扩容两倍
}
ph->a[ph->size++] = x;
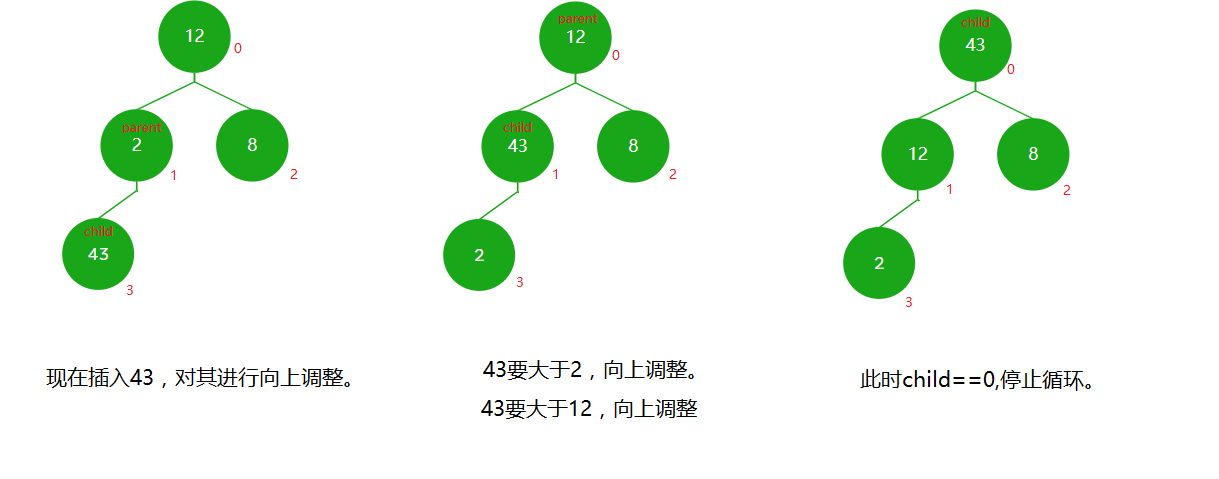
//因为要实现大根堆,如果入堆元素大于前面的元素,就要把它向上调整。
AdjustUp(ph->a, ph->size - 1);//第一次参数是要调整的数据元素,第二个参数是入堆元素的下标。
}
- 向上调整
//向上调整
void Swap(HPDataType* p1, HPDataType* p2)
{
HPDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void AdjustUp(HPDataType* a, int child)
{
//得到父节点的下标
int parent = (child - 1) / 2;
while (child > 0)//当子节点爬到下标为0的位置,就达到顶部了,此时可以停止循环
{
//比较父节点和子节点,谁大谁上去
//让大的节点不断往上爬
if (a[chil] > a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
- 出堆
疑惑
(1)
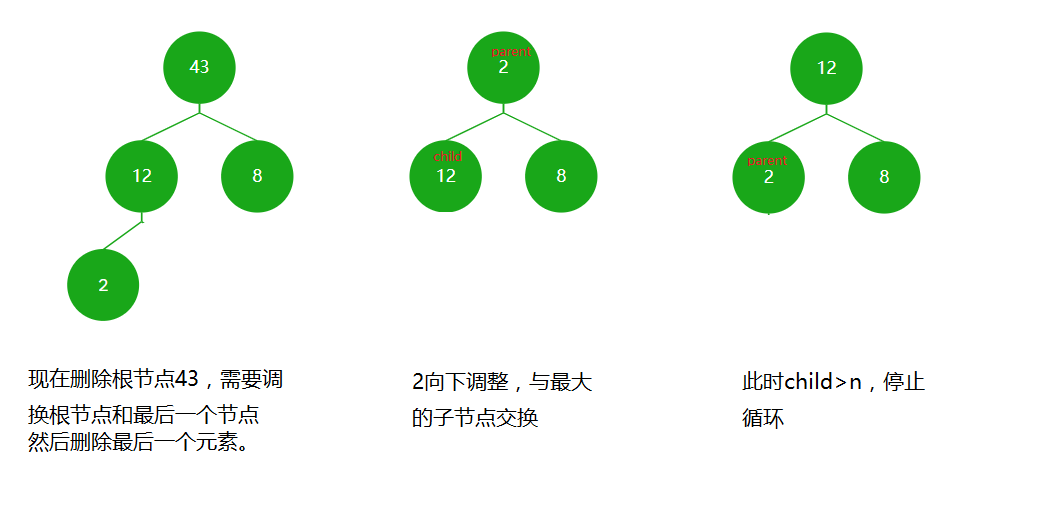
出堆其实就是弹出根节点。但我们要考虑弹出根节点后,后面的数据要如何处理?将数据往前移动?这样数据间的关系就全乱了,且所有数据往前移效率低(O(N^2))。
正确的做法是交换堆顶元素和最后一个元素,然后删除最后一个元素,然后将堆顶元素向下调整。
(2)
为什么要弹出根节点?弹出最后一个元素岂不是更简单?这就涉及到堆的应用。我们所写的是大根堆,根结点是这组数据的最大值,弹出根节点后,向下调整可以得到次大值,然后再弹出根节点。就这样,我们就得到这组数据的前n个最大值,比如得到年纪前50名,得到产品销量前100名。由此可见,弹出根结点是非常有用的。
代码实现
//堆空
bool HeapEmpty(HP* ph)
{
assert(ph);
return ph->size == 0;
}
//出堆
void HeapPop(HP* ph)
{
assert(ph);
//首先判断堆是否为空
assert(!HeapEmpty(ph));
//交换堆顶元素和最后一个元素
Swap(&ph->a[0], &ph->a[ph->size - 1]);
//删除最后一个元素
ph->size--;
//向下调整
AdjustDown(ph->a, ph->size, 0);
//第一个参数是要调整的数据,第二个参数是数据的个数,第三个参数是要调整的位置
}
- 向下调整
//向下调整(条件:左右子树都是大根堆或者小根堆)
void AdjustDown(HPDataType* a, int n, int parent)
{
int child = 2 * parent + 1;//先得到左孩子
while (child < n)//当子节点的下标大于元素个数时停止循环
{
//如果右孩子存在且大于左孩子,那么就换成右孩子与父节点比较
if (child + 1 < n && a[child + 1] > a[child])
{
++child;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
- 堆顶
//堆顶
HP* HeapTop(HP* ph)
{
assert(ph);
//首先判断堆是否为空
assert(!HeapEmpty(ph));
return ph->a[ph->size - 1];
}
- 打印前K个元素
//打印前K个元素
void PrintK(HP* ph, int k)
{
while (!HeapEmpty(ph) && k--)
{
printf("%d ", HeapTop(ph));
HeapPop(ph);
}
printf("\n");
}
- 销毁
//销毁
void HeapDestroy(HP* ph)
{
assert(ph);
free(ph->a);
ph->a = 0;
ph->capacity = 0;
ph->size = 0;
}
2.3 堆排序
了解堆的基本操作后,就可以实现堆排序。
//法一
//堆排序(以排升序为例)
void HeapSort(int* a, int n)
{
//建堆(大根堆或者小根堆)
for (int i = 1; i < n; i++)
{
AdjustUp(a, i);//从下标为1的元素不断插入,从而向上调整
}
//建大根堆后,就交换根结点和最后一个元素,每次交换都将最大值放在数据的最后面
int end = n - 1;
while (end > 0)
{
Swap(&a[end], &a[0]);//交换最大值和最后一个元素
AdjustDown(a, end, 0);//交换后最后一个元素不参与调整,所有元素个数只有end个
//每次调整后都会将最大值放在根节点的位置
--end;
}
}
//法二
void HeapSort(int* a, int n)
{
//从最后一个元素的父节点开始向下调整
//目的是建成大根堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[end], &a[0]);
AdjustDown(a, end, 0);
--end;
}
}
时间复杂度
这两种方法唯一的不同就是法一前面是向上调整,法二前面是向下调整。要比较两种方法的时间复杂度就得比较向下调整和向上调整的时间复杂度。
-
向下调整的时间复杂度是O(N)

-
向上调整的时间复杂度是O(NlogN)
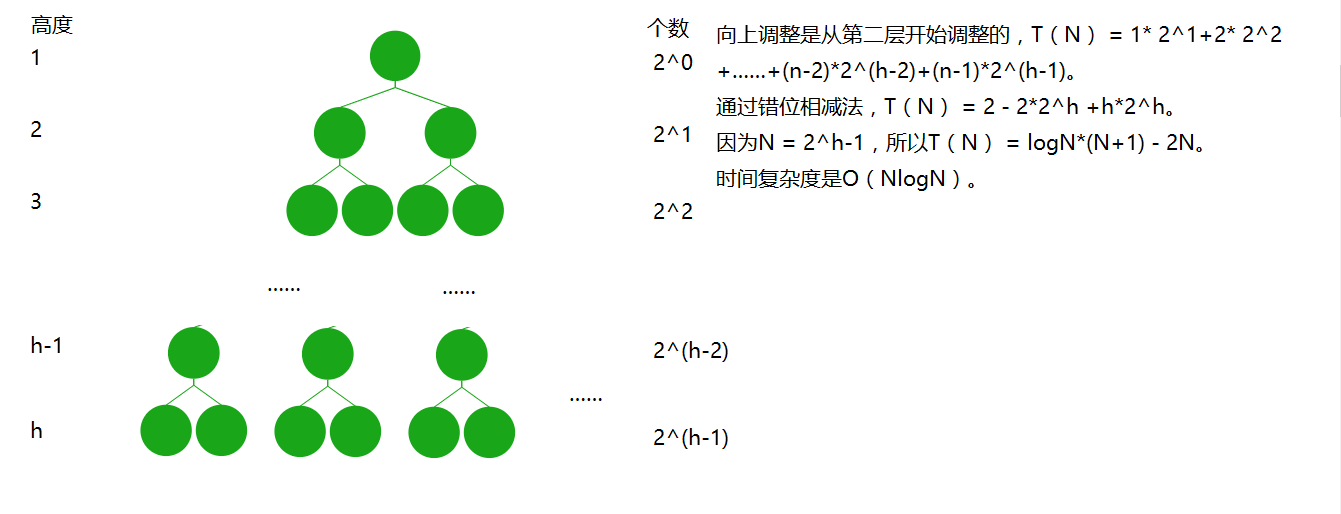
咋一看好像第二种方法时间复杂度更牛,但实际上这两种方法的时间复杂度都是O(NlogN)。我们讨论的只是向下调整和向上调整。
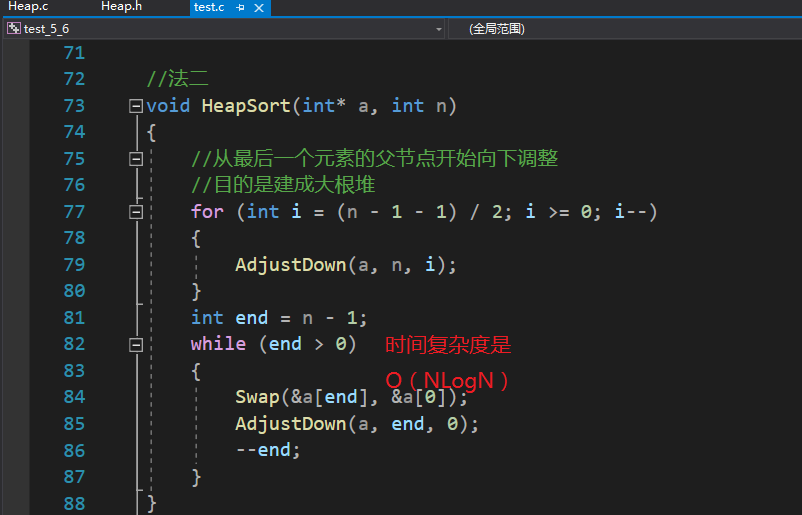
总的来说,堆排序的时间复杂度是O(NLogN)。两种方法都在这个量级,但第二种方法稍微高一点点。
3. 堆排序(topK问题)
找出N个数中最大的(或最小的)前K个数。
有两种方法:
法一:建N个大根堆,然后PopK次就可以。
法二:建有K个数的小根堆,遍历剩下的数据,如果数据比堆顶元素大,就替换它,然后向下调整,最后这个小根堆的数据就是最大的前K个。
这里主要用法二
void PrintTopK(const char* file, int k)
{
//首先要建立小根堆
int* topk = (int*)malloc(sizeof(int) * k);
if (topk == NULL)
{
perror("malloc failed");
return;
}
//从文件中读取K个数据
FILE* f = fopen(file, "r");
if (f == NULL)
{
perror("fopen failed");
return;
}
for (int i = 0; i < k; i++)
{
fscanf(f, "%d", &topk[i]);
}
//建小堆(之前写的向下调整是调整大根堆,只需修改其中一些>或者<即可)
for (int i = (k - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(topk, k, i);
}
//将剩下的n-k个元素依次与根节点比较,比它大就入堆且向下调整
//这样将大的元素往下沉,小的元素不断换掉,最终只剩下最大的K个元素
int val = 0;
int ret = fscanf(f, "%d", &val);
while (ret != EOF)
{
if (val > topk[0])
{
topk[0] = val;
AdjustDown(topk, k, 0);
}
ret = fscanf(f, "%d", &val);
}
for (int i = 0; i <k; i++)
{
printf("%d ", topk[i]);
}
fclose(f);
}
void CreateData()
{
int n = 1000;
srand(time(0));
const char* file = "TestData.txt";
FILE* f = fopen("TestData.txt", "w");//以写的形式打开
if (f == NULL)
{
perror("fopen fail");
return;
}
for (int i = 0; i < n; i++)
{
int x = rand() % 1000;//获得0~999的数字
fprintf(f, "%d ", x);
}
fclose(f);
}