warning: 本文仅为个人思考，非常不严谨甚至可能会出现严重错误，请读者仔细甄别，若本文真的存在严重错误，恳请评论区纠正，我看到将会考虑修改或者删除文章

纯比例控制存在稳态误差是由其本质（控制逻辑？）决定的
以极端例子纯增益系统G(s)=1为例（该系统输出完全等于输入）
当比例增益太小时，系统会存在稳态误差，假设Kp=0.5，要调节的目标值是1，初始值为0，则
第一次计算：
$e=1-0=1$
$u=K_P\ast e=0.5$

第二次计算：
$e=1-0.5=1$
$u=K_P\ast e=0.25$
（还没到目标值甚至还降下来了，这时候比例环节就非常反常识）

第二次计算：
$e=1-0.5=1$
$u=K_P\ast e=0.25$
（还没到目标值甚至还降下来了，这时候比例环节就非常反常识）

第三次计算：
$e=1-0.25=0.75$
$u=K_P\ast e=0.327$
（这次计算重新升上去了，但是甚至还不如第一次计算靠目标值近）

后面的计算以此类推 ，如下图所示

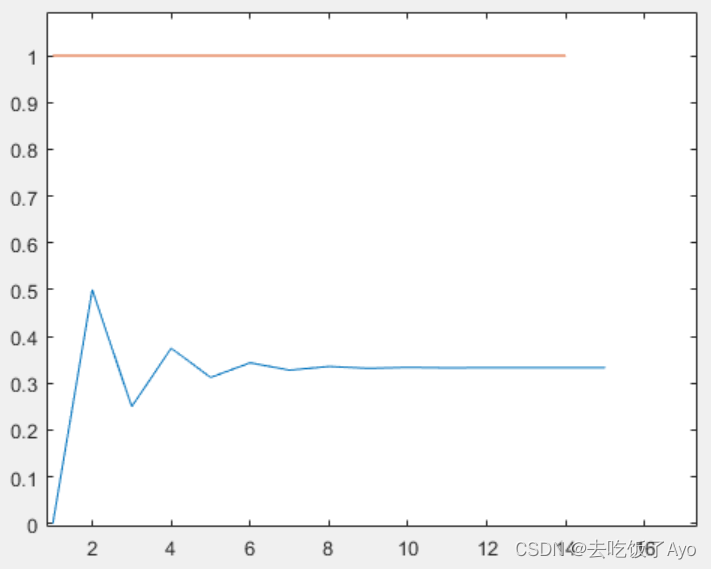
纯比例控制的控制逻辑似乎就不是控制输出到目标值。
说到比例控制，可能会想到这个下图

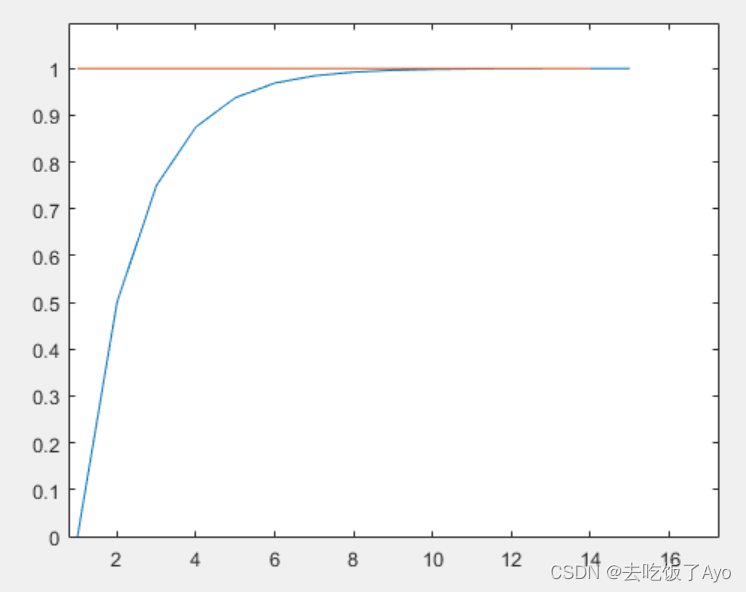
但这并不是位置式PID的纯比例控制
位置式的纯比例控制公式为
$u=K_P\ast e$
而上图的公式为
$\Delta u=K\ast e$

这是增量式PID的积分部分，甚至不是PID，PID不可能只有积分项而没有比例项目
$$u\left(t\right)=K_P\left(e\left(t\right)+\frac{1}{T_I}{\int }_0^{t}e\left(\tau \right)d\tau +T_D\frac{de\left(t\right)}{dt}\right)$$
$K_I=\frac{K_P}{T_I}$

总结

纯比例环节稳态误差是由其本质决定的，其只能迅速缩小误差。如果$K_P$过小，则不能消除稳态误差，如果加大$K_P$会导致系统不稳定，所以纯比例环节不能消除稳态误差。