2.3.1 队列及顺序存储实现

什么是队列

概念：

和堆栈一样，是一种受限的线性表。

特性：

插入和删除操作：只能在一端插入，在另一端删除
数据插入：称为入队（AddQ）
数据删除：称为出队（DeleteQ）
特性：先进先出，First In First Out——FIFO

队列的抽象数据类型描述

类型名称：队列

数据对象集：一个有0~N个元素的有穷线性表

操作集：长度为MaxSize的队列Q∈Queue，队列元素item∈ElementType

Queue CreateQueue(int MaxSize) 生成长度为MaxSize的空队列
int IsFullQ(Queue Q,int MaxSize) 判断队列Q是否已满
void AddQ(Queue Q,ElementType item) 将数据元素item插入队列Q中
int IsEmpty(Queue Q) 判断队列Q是否为空
ElementType DeleteQ(Queue Q) 将队列头数据元素从队列中删除并返回

队列的顺序存储实现

通常使用一个一维数组、一个记录队列头元素位置的变量front、一个记录队列尾元素的变量rear来实现队列。

规律：front和rare初始都为-1.插入一个元素，rear加一，删除一个元素时，front加一，删除时相当于把队列向后移动.

假设一个极端情况：队列容量为6，每插入一个元素之后紧接着就删除它，当处理了6个元素之后，队头队尾都到了最后一位，现在想要插入元素就变得不可能了。于是我们提出一个概念叫循环队列：

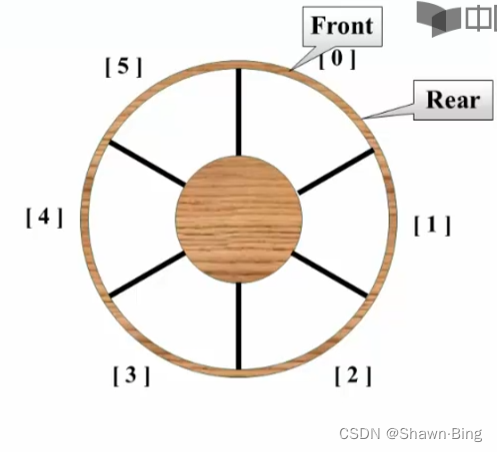
缺点：开始时，front==rear，为空。放满元素后二者也相等，于是队列的空和满无法判断。判断空和满是通过两个变量位置的距离。二者的距离只有0、1、2、3、4、5这6种。而队列装载元素的状态有0、1、2、3、4、5、6这7种。用n种的状态来区分n+1种的状态，显然从数学上来说是有缺陷的。

解决方案：

1.使用额外标记：Size或Tag域

加入一个元素时Size+1，删除时-1，根据Size为0或N来判断队列的空和满
加入元素Tag为1，删除元素Tag为0，当front==rear时查看Tag值，即最后一次操作是插入还是删除，如果是插入元素说明是队满，删除说明是队空。

2.虽然申请n个位置的空间，但仅使用n-1个（本案例使用方案）

//1.入队
void AddQ(Queue PtrQ,ElementType item)
{
//具体实现循环队列中“循环”的要素，若要让第0号位成为第6号位，
//就用5的下1位对6求余
    if( (PtrQ->rear+1)%MaxSize == PtrQ->front ){
        printf("队列满");
        return;
    }
    PtrQ->rear = (PtrQ->rear+1)%MaxSize;
    PtrQ->Data[PtrQ->rear] = item;
}

//2.出队
ElementType DeleteQ(Queue PtrQ){
    if( PtrQ->front == PtrQ->rear ){
        printf("队列空");
        return ERROR;
    }else{
        PtrQ->front = (PtrQ->front+1)%MaxSize;
        return PtrQ->Data[PtrQ->front];
    }
}

2.3.2 队列的链式存储实现

链式存储也可以用一个单（向）链表实现。插入和删除分别在链表两头进行。front指向链表头；rear指向链表尾

struct Node{
    ElementType Data;
    struct Node *Next;
};

struct QNode{
    struct Node *rear;
    struct Node *front;
};

typedef struct QNode *Queue;
Queue PtrQ;

1.队列出队(没有头结点的链表)
ElementType DeleteQ(Queue PtrQ){
    struct Node *FrontCell;
    ElementType FrontElem;

    if( PtrQ->front == NULL ){
        printf("队列空");
        return ERROR;
    }

    FrontCell = PtrQ->fornt;//找到头结点

    //如果只有一个元素
    if( PtrQ->front == PtrQ->rear ){
        //删除元素后队列置空，两个都要指向NULL
        PtrQ->front == PtrQ->rear = NULL;
    }else{
        //不止一个元素，front往后移
        PtrQ->front == PtrQ->front->Next;
    }

    FrontElem = PtrQ->Data;
    free(FrontCell);//释放空间
    return FrontElem;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/496863.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！