考研数据结构大题整合
目录
- 考研数据结构大题整合
- 一、ZYL组
- ZYL组一
- ZYL组二
- ZYL组三
- ZYL组四
- ZYL组五
- ZYL组六
- ZYL组七
- ZYL组八
一、ZYL组
ZYL组一
1.一棵树有度为i的结点ni 个(i=1,2,3,…m), 求叶结点的个数.(10分)
∑ i = 1 m ( n i ∗ i ) + 1 − ∑ i = 1 m ( n i ) \sum_{i=1}^m(n_i *i)+1-\sum_{i=1}^m(n_i) i=1∑m(ni∗i)+1−i=1∑m(ni)
2、已知带权连通图G=(V,E)的邻接表如图所示,请画出该图,并分别以深度优先和广度优先遍历之,写出遍历结点序列,并画出该图的一个最小生成树。其中表结点的三个域各为: (10分)
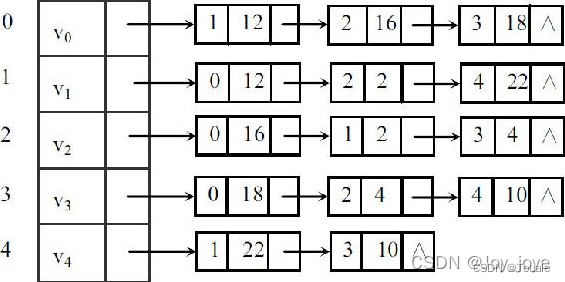
深度:v0 v1 v2 v3 v4
广度: v0 v1 v2 v3 v4
3.证明:任一棵满二叉树T中分支数B满足B=2(n0-1),(其中n0为叶结点数)。(10分)
因 为 树 T 为 满 二 叉 树 , 因 此 不 存 在 度 为 1 的 结 点 : 2 n 2 = n 0 + n 2 − 1 n 2 = n 0 − 1 = > n = n 0 + n 2 = 2 n 0 − 1 = > 分 支 数 B = 2 n 0 − 1 − 1 = 2 ( n 0 − 1 ) 因为树T为满二叉树,因此不存在度为1的结点: \newline 2n_2 = n_0+n_2-1 \\ n_2=n_0-1 \\ => n = n_0+n_2 = 2 n_0-1\\ => 分支数B= 2 n_0-1 -1 = 2(n_0-1) 因为树T为满二叉树,因此不存在度为1的结点:2n2=n0+n2−1n2=n0−1=>n=n0+n2=2n0−1=>分支数B=2n0−1−1=2(n0−1)
五、程序填空/写程序结果或程序功能 (20分)
1、程序填空: (5分)
void SelectSort(Datatype R[ ],int n)
//用直接选择排序法对R[0]---R[n-1]排序
{ int i,j,small;
datatype temp;
for(i=0;i<n-1;i++)
{ small=i;
for(j=i+1;j<n;j++) //寻找排序码最小的元素
{ if(________) small=j;}
if(small!=i)
{ temp=R[i]; R[i]=R[small]; R[small]=temp; }
}
}
解:
R[j] < R[small]
2、分析下面程序段的复杂度.(5分)
for (i = 1; i <= n; i++)
{
for (j = 1; j <= n; j++)
b[i, j] = 0;
{
sum = 0;
for (k = 1; k <= n; k++)
{
sum = sum + a[i, k] * a[k, j];
}
}
}
b[i, j] = sum;
end;
该程序段的复杂度为__ O ( n 3 ) O(n^3) O(n3)____.
3、一棵具有n个结点的完全二叉树以一唯数组作为存储结构,对该完全二叉树进行前序遍历的非递归算法如下:写出空格部分的内容。 (10分)
// preorder(R) 前序遍历二叉树R
int R[n];
{
int root; // root 为数组的下标
seqstack *s; //*s 为一指针栈,类型为seqstack
s->top = -1; // s栈置空
root = 1; // 从数组第一单元开始扫描遍历
while ((root <= n) || (s->top > -1))
{
while (______________)
{
cout << R[root];
_________;
s->data[s->top] = root; // 保留结点
root = 2 * root; // 遍历左子树
}
if (__________) // 栈非空,遍历右子树
{
root = s->data[s->top] * 2 + 1;
___________;
}
}
}
解答:
1、root <= n
2、top ++
3、top > -1
4、top --
答案说是top,我觉得应该是s->top,,,
ZYL组二
四、计算题/画图题/证明题 (30分)
1.试为下列二叉树建立后序线索,画出相应的后序线索二叉树.(10分)
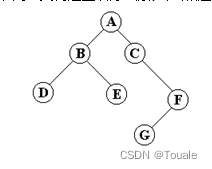
2.已知某电文中共出现10种不同的字母,各个字母出现的频率分别为A:8, B:5, C:3, D:2, E:7, F:23, G:9, H:15, I:3, J:35 ,现在对这段电文用三进制进行编码(即码字由0,1,2组成),问电文编码总长度最少有多少位?并画出图(10分)
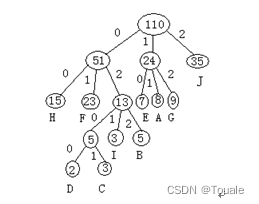
电文用三进制进行编码为:
A: 11 B: 022 C: 0201 D: 0200 E: 10
F: 01 G: 12 H: 00 I: 021 J: 2
电文编码总长度为:35*1+(8+7+23+9+15)*2+(3+5)*3+(2+3)*4=203
3.证明:前序序列和中序序列、后序序列和中序序列可唯一确定一棵二叉树,而前序序列和后序序列则不能。(10分)
用数学归纳法
五、程序填空/写程序结果或程序功能 (20分)
1、程序填空: (7分)
用链表表示的数据的简单选择排序,结点的域为数据域data,指针域next,链表首指针为head,链表无头指针。
Selectsort(head)
{
p = head;
while (p___1______)
{
q = p;
r = _____2_____;
while (______3______)
{
if (_______4_____)
q = r;
r = ______5______;
}
tmp = q->data;
q->data = ____6_____;
p->data = tmp;
p = ______7____;
}
}
解:
1、!= null
2、p->next
3、r != null
4、q->data>r->data
5、r->next
6、p->data
7、p->next
2、分析下面程序段的复杂度:(5分)
x = n; // n>1
y = 0;
while (x >= (y + 1) * (y + 1))
{
y = y + 1;
}
该程序段的复杂度为________ O ( n 1 / 2 ) O(n^{1/2}) O(n1/2)____________。
3、中序遍历线索二叉树算法(树的结点有5个域:数据域data,左右孩子域lchild, rchild和左右标志域ltag, rtag,规定标志域1是线索,0是指向孩子的指针。) (8分)
void inorder(Hbitree *t)
{
Hbitree *p;
p = t;
if (p____1_____)
{
while (p______2_____)
p_____3______; // 找开始结点
while (p____4______)
{
cout << p->data;
p = inordernext(p); // 调用函数找中序后继
}
}
}
解答
1、!= null
2、->ltag==0 // 走到最左下角的节点
3、= p->lchild
4、!= null
ZYL组三
四、计算题/画图题/证明题 (30分)
1、对于如图所示的有向图,试写出:
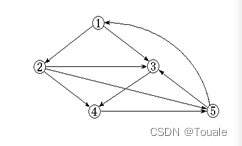
(1) 从顶点①出发按深度方向周游所得到的深度优先生成树;
(2) 从顶点②出发按广度方向周游所得到的广度优先生成树;
(3) 能否找出一个拓扑有序的序列?若能,给出一个拓扑有序的序列。.(10分)
解答:
(1)、1 2 3 4 5
(2)、3 4 5 1
(3)、不能
2.设散列表为HT[13], 散列函数为H(key)=key%13。用闭散列法解决冲突,对下列关键码序列12,23,45,57,20,03,78,31,15,36造表。采用线性探查法寻找下一个空位, 画出相应的散列表, 并计算等概率下检索成功的平均比较次数和检索不成功的平均比较次数。(10分)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 78 | 15 | 3 | 57 | 45 | 20 | 31 | 23 | 36 | 12 |
成功:
(
4
+
10
)
/
10
=
1.4
(4+10)/10 = 1.4
(4+10)/10=1.4
失败:
(
2
+
1
+
3
+
2
+
1
+
5
+
4
+
3
+
2
+
1
+
5
+
4
+
3
)
/
13
=
36
/
13
(2+1+3+2+1+5+4+3+2+1+5+4+3)/13=36/13
(2+1+3+2+1+5+4+3+2+1+5+4+3)/13=36/13
点评:失败时走到最后面若没有空还要继续往后一直走到有空,可以循环到头节点
3.如果一棵树有n1个度为1的结点, 有n2个度为2的结点, … , nm个度为m的结点, 试问有多少个度为0的结点? 试推导之。(10分)
写过了
五、程序填空/写程序结果或程序功能 (20分)
1、程序填空: (5分)
二分查找算法实现
int BinSeach(Datatype a[], int n, Keytype key)
{
int low = 0, high = n - 1, mid;
while (low <= high)
{
mid = _____1________;
if (____2________)
return mid;
else if (_____3________)
_____4______;
else
_____5_______;
}
return -1;
}
解答
1、(low + high) / 2
2、a[mid].key == key
3、a[mid].key <k
4、high = mid - 1
5、low = mid + 1
感觉怪怪的,凑合吧
2、对连通图从顶点v开始用visit()广度优先访问 (8分)
void AdjMWGraph::BroadFirstSearch(const int v, int visited[]);
void visit(VerT item))
{
VerT u, w;
SeqQueue queue;
visit(GetValue(v));
visited[v] = 1;
queue.QInsert(v);
while (!queue.QueueEmpty())
{
u = _______1________;
w = GetFirstNeighbor(u);
while (_____2_____)
{ if(_____3______])
{
visit(GetValue(w));
_____4______;
queue.QInsert(w);
}
w = GetNextNeighbor(u, w);
}
}
}
解答:
1、queue.QDelete()
2、w!=-1
3、visited[w] == 0;
4、 visited[w] = 1;
3、读程序,写出其功能及采用的算法 (7分)
long fib2(int n)
{
if (n == 0 || n == 1)
return n;
else
{
long int oneBack = 1, twoBack = 0, current;
for (int i = 2; i <= n; i++)
{
current = oneBack + twoBack;
twoBack = oneBack;
oneBack = current;
}
return current;
}
}
解答:
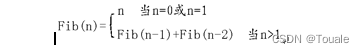
ZYL组四
四、计算题/画图题/证明题 (30分)
1、 画出具有3个结点的二叉树的所有不同形态,并判断下列论述是否正确,为什么?
(1) 二叉树是一种特殊的树;
(2) 度为2的树是一棵二叉树;
(3) 度为2的有序树是一棵二叉树。
2、 已知一棵度为m的树中,有 个度为1的结点,有 个度为2的结点,……有 个度为m的结点,请推导出该树中叶子结点的数目。
3、 对于如下图所示的带权无向图,用图示说明:
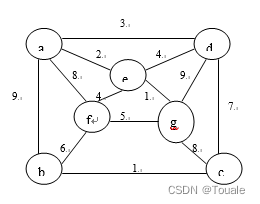
(1) 利用Prim算法从顶点a开始构造最小生成树的过程;
(2) 利用Kruskal算法构造最小生成树的过程;
五、程序填空/写程序结果或程序功能 (20分)
程序填空:
1、对连通图从顶点v开始用visit()深度优先访问
void AdjMWGraph::DepthFirstSearch(const int v,int visited[],void visit(VerT item))
{ visit(GetValue(v));
________________________(1);
int w=GetFirstNeighbor(v);
while(________________________(2))
{ if(________________________(3)) DepthFirstSearch(w,visited,visit);
w=________________________(4);
}
}
2、希尔排序
void ShellSort(Datatype a[],int n)
{
int numOfD=3;
int d[3]={6,3,1};
int i,j,k,m,span;
Datatype temp;
for(m=0;m<numOfD;m++)
{
span=d[m];
for(k=0;k<span;k++)
{
for(i=k;i<n-span;i=i+span)
{
____________________(1);
____________________(2);
while(j>-1&&temp.key<=a[j].key)
{
____________________(3);
____________________(4);
}
a[j+span]=temp;
}
}
}
六、算法设计 (10分)
从一个有n个人的团体中抽出k (k<=n) 个人组成一个委员会,问:共有多少种构成方法?分析给出求解此问题的递推定义式和递归算法。
ZYL组五
四、计算题/画图题/证明题 (30分)
1、试计算以下求和程序中所有语句的总执行次数。
float sum( float a[ ], int n )
{
float s = 0.0;
for ( int i = 0; i < n; i++ )
s += a[i];
return s;
}
2、顺序表的插入和删除要求仍然保持各个元素原来的次序。设在等概率情形下, 对有127个元素的顺序表进行插入, 平均需要移动多少个元素? 删除一个元素, 又平均需要移动多少个元素?
3、已知一棵二叉树的前序遍历结果是ABECDFGHIJ, 中序遍历结果是EBCDAFHIGJ, 试画出这棵二叉树。
4、一项工程由六个子工程p1, p2, … p6组成。这些子工程之间有下列关系:p1 < p2, p3 < p6, p4 < p3, p2 < p6, p4 < p5, p1 < p3, p5 < p6。符号“<”表示“领先于”的关系。例如,p2 < p6表示p2完成后p6才能开始。试给出该工程的三种可能的施工顺序。
五、程序填空/写程序结果或程序功能 (20分)
1、假定数组A[arraySize]中有多个零元素, 试写出一个函数, 将A 中所有的非零元素依次移到数组A的前端A[i] (0≤ i ≤arraySize)。
void compact(data_type A[],int ArraySize)
{
int free =0,i; //非零元素存放地址
for(i=0;________;i++) //检测整个数组
{
if(A[i] != 0 ) //发现非零元素
{
if( i!=free )
{
________;
a[i] =0;
}
________;
}
}
}
2、下列程序是一个两路归并算法merge,只需一个附加存储。设算法中参加归并的两个归并段是A[0] A[n-1] 和B[0] B[m-1],归并后结果归并段放在原地。数据结构定义为:
typedef float datatype;
算法描述如下:
void merge(datatype &A[], datatype &B[], int n, int m)
{
int i, j; datatype temp; for (i = 0; i < n; i++)
{
if (A[i] > B[0])
{
________;
for (j = n - 2; j >= i; j--)
A[j + 1] = A[j]; ________; if (temp <= B[1]) ________; else
{
for (j = 1; j < m; j++)
{
if (temp > B[j])
________; else
{
________; break;
}
}
}
}
}
}
3、请编写一个算法,在基于单链表表示的待排序排序码序列上进行直接选择排序。
ListNode *selectSort(ListNode *first)
{
ListNode *h = first, *p, *q, *r, *s;
ListNode *f = NULL;
while (h != NULL)
{ // 原始链表未扫描完
p = s = h;
q = r = NULL;
while (p != NULL)
{ // 寻找最大结点s
if (p->data > s->data)
{
s = p;
r = q;
}
// 记忆当前找到的排序码最大结点
q = p;
______________;
}
if (s == h)
h = h->link;
else
r->link = s->link;
______________;
f = s; // 结点s前插
}
return f;
}
六、算法设计 (10分)
试设计一个实现下述要求的查找运算函数Locate(L, x)。设有一个带表头结点的双向链表L,每个结点有4个数据成员:指向前驱结点的指针prior、指向后继结点的指针next、存放数据的成员data和访问频度freq。所有结点的freq初始时都为0。每当在链表上进行一次Locate (L, x)操作时,令元素值为x的结点的访问频度freq加1,并将该结点前移,链接到与它的访问频度相等的结点后面,使得链表中所有结点保持按访问频度递减的顺序排列,以使频繁访问的结点总是靠近表头。
ZYL组六
四、计算题/画图题/证明题 (30分)
- 指出算法的功能 并求出其时间复杂度。
void matrimult(int a[][], int b[][], int c[][], int M, int N, int L)
{
// 数组a[M][N]、b[N][L]、c[M][L]均为整型数组
int i, j, k;
for (i = 0; i < M; i++)
for (j = 0; j < L; j++)
{
c[i][j] = 0;
for (k = 0; k < N; k++)
c[i][j] += a[i][k] * b[k][j];
}
}
2、对于一个nXn的矩阵A的任意矩阵元素a[i][j],按行存储时和按列存储时的地址之差是多少。(若设两种存储的开始存储地址LOC(0, 0) 及元素所占存储单元数d相同)
3、设散列表的长度m = 13;散列函数为H (K) = K % m,给定的关键码序列为19, 14, 23, 01, 68, 20, 84,27, 55, 11,试画出用线性探查法解决冲突时所构造的散列表。并求出在等概率的情况下,这种方法的搜索成功时的平均搜索长度和搜索不成功时的平均搜索长度。
4、设一有向图如下所示,请问该有向图是否为强连通图,并画出该有向图所有的强连通分量。
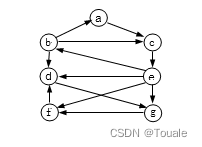
五、程序填空/写程序结果或程序功能 (20分)
1、针对如下算法,回答问题:
template <class T>
void unknown(T A[], int n)
{
int free = 0;
for (int i = 0; i < n; i++)
if (A[i] != 0)
{
if (i != free)
{
A[free] = A[i];
A[i] = 0;
}
free++;
}
}
(1) 说明若数组A[ ] = {12, 24, 0, 38, 0, 0, 0, 0, 29, 0, 45, 0}, n = 12,算法执行的结果。
(2) 说明算法的功能是什么。
2、若设单链表结点的结构为ListNode = (data, link),阅读以下函数:
void unknown(LinkList Ha)
{
// Ha为指向带头结点的单链表的头指针,且头结点的data域中含元素o
if (Ha != NULL)
{
unknown(Ha->link);
cout << Ha->data << endl;
}
}
若线性表L = ( a, b, c, d, e, f, g ),则执行语句unknown (L) 之后输出的结果是_________________。
3、写出下列程序段的输出结果:
void main()
{
queue Q;
char x = 'e', y = 'c';
Q.EnQueue('h');
Q.EnQueue('r');
Q.EnQueue(y);
Q.DeQueue(Q, x);
Q.EnQueue(x);
Q.DeQueue(x);
Q.EnQueue('a');
while (!Q.IsEmpty())
{
Q.DeQueue(y);
cout << y;
}
cout << y << endl;
}
输出结果:______________________
4、已知二叉树中的结点类型用BinTreeNode表示,被定义为:
struct BinTreeNode
{
char data;
BinTreeNode *leftChild, *rightChild;
};
char BTM(BinTreeNode *BT)
{
static char max = 0;
if (BT != NULL)
{
char k1, k2;
k1 = BTM(BT->leftChild);
k2 = BTM(BT->rightChild);
if (k1 > max)
max = k1;
else if (k2 > max)
max = k2;
else if (BT->data > max)
max = BT->data;
}
return max;
}
其中data为结点值域,leftChild和rightChild分别为指向左、右子女结点的指针域。假定一棵二叉树采用链接存储,它的广义表表示为r (b (, d (f, g) ), t (e) ),rt, bt, dt和et指针变量分别保存指向r, b, d和e结点的指针值,则:
(1)执行BTM (rt) 调用后,得到的函数值为________;
(2)执行BTM (bt) 调用后,得到的函数值为________;
(3)执行BTM (dt) 调用后,得到的函数值为________;
(4)执行BTM (et) 调用后,得到的函数值为________;
六、算法设计 (10分)
写出二路归并排序的算法程序。
ZYL组七
四、 计算题/画图题/证明题 (30分)
1、设有一个连通网络如图所示。试按如下格式,应用Kruskal算法给出在构造最小生成树过程中顺序选出的各条边。
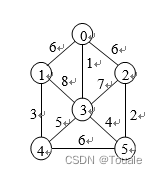
( 始顶点号,终顶点号, 权值 )
( , , )
( , , )
( , , )
( , , )
( , , )
2、设有一个1010的对称矩阵A,将其下三角部分按行存放在一个一维数组B中,A[0][0]存放于B[0]中,那么A[8][5]存放于B中什么位置。
3、假定一个线性序列为 ( 56, 27, 34, 95, 73, 16, 50, 62, 65 ),根据此线性序列中元素的排列次序生成一棵二叉搜索树,求出该二叉搜索树的高度(假定树根结点的高度为0)、度为2的结点个数和叶子结点个数。
高度:_____________
度为2的结点个数:____________
叶子结点个数:____________
4、试对下图所示的AOE网络
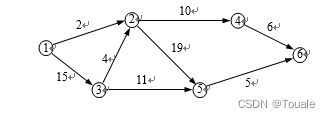
(1) 这个工程最早可能在什么时间结束。
(2) 确定哪些活动是关键活动。画出由所有关键活动构成的图,指出哪些活动加速可使整个工程提前完成。
五、 程序填空/写程序结果或程序功能 (20分)
1、若设单链表结点的结构为ListNode = (data, link),阅读以下函数::
int unknown(ListNode *Ha)
{
// Ha为指向带头结点的单链表的头指针
int n = 0;
ListNode *p = Ha->link;
while (p != NULL)
{
n++;
p = p->link;
}
return n;
}
若线性表L = ( a, b, c, d, e, f, g ),则执行语句unknown (L) 之后输出的结果是什么。
2、已知二叉树中的结点类型用BinTreeNode表示,被定义为:
struct BinTreeNode
{
ElemType data;
BinTreeNode *leftChild, *rightChild;
};
其中data为结点值域,leftChild和rightChild分别为指向左、右子女结点的指针域。下面函数的功能是返回二叉树BT中值为x的结点所在的层号,请在划有横线的地方填写合适的内容。
int NodeLevel(BinTreeNode *BT, ElemType &x)
{
if (BT == NULL)
return –1; // 空树的层号为-1
else if (BT->data == x)
return 0; // 根结点的层号为0
else
{
int c1 = NodeLevel(BT->leftChild, x); // 向子树中查找x结点
if (c1 >= 0)
_________(1)
_________;
int c2 = _________(2) __________;
___________(3)
____________;
else return -1; // 在树中不存在x结点返回-1
}
}
(1) _____________________________________________
(2) _____________________________________________
(3) _____________________________________________
3、下面给出一个排序算法,它属于数据表类的成员函数,其中currentSize是数据表实例的当前长度,Vector[ ] 是存放数据表元素的一维数组。
template <class T>
void dataList<T>::unknown()
{
T temp;
int i, j, n = currentSize;
for (i = 1; i < n; i++)
if (Vector[i].key < Vector[i - 1].key)
{
temp = Vector[i];
Vector[i] = Vector[i - 1];
for (j = i - 2; j >= 0; j--)
if (temp.key < Vector[j].key)
Vector[j + 1] = Vector[j];
else
break;
Vector[j + 1] = temp;
}
}
(1) 该算法执行什么功能?
(2) 针对有n个数据对象的待排序的数据表,算法的排序码比较次数和对象移动次数最好是多少?最坏是多少?
六、算法设计 (10分)
- 已知二叉树中的结点类型用BinTreeNode表示,被定义为:
struct BinTreeNode
{
char data;
BinTreeNode *leftChild, *rightChild;
};
其中data为结点值域,leftChild和rightChild分别为指向左、右子女结点的指针域,根据下面函数声明编写出求一棵二叉树高度的算法,该高度由函数返回。假定根结点的层次为0,参数BT初始指向这棵二叉树的根结点。
int BTreeHeight ( BinTreeNode* BT );
ZYL组八
四、 计算题/画图题/证明题 (30分)
1、画出下列广义表的有序树形表示。
(1) D (A ©, B (e), C (a, L (b, c, d) ) )
2、假定一棵普通树的广义表表示为a (b (e), c (f (h, i, j), g), d),分别写出先根、后根、按层遍历的结果。
先根:__________________________
后根:__________________________
按层:__________________________
3、设有向图G如图所示。试画出从顶点V0开始进行深度优先搜索和广度优先搜索得到的DFS生成森林和BFS生成森林。
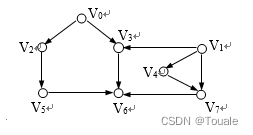
4、判断以下序列是否是最小堆?如果不是, 将它调整为最小堆。
(1) { 100, 86, 48, 73, 35, 39, 42, 57, 66, 21 }
(2) { 12, 70, 33, 65, 24, 56, 48, 92, 86, 33 }。
五、 程序填空/写程序结果或程序功能 (20分)
1、设顺序表SeqList具有下列操作:
int Length() const; // 计算表长度
T Remove(); // 删除当前表项,置下一表项为当前表项
T First(); // 取表中第一个表项的值,置为当前表项
T Next(); // 取当前表项后继表项的值,置为当前表项
试针对如下算法,回答问题:
#include <iostream.h>
#include “SeqList.h”
template <T>
void unknown(SeqList<T> *L, T s, T t)
{
if (!L->Length() || s >= t)
{
cerr << “List is empty or parameters are illegal !” << endl;
exit(1);
}
int i = 0;
T temp = L->First();
while (i < L->Length())
if (temp >= s && temp <= t)
L->Remove();
else
{
temp = L->Next();
i++;
}
}
(1) 说明若顺序表中存放的数据为 { 29, 38, 47, 16, 95, 64, 73, 83, 51, 10, 0, 26 },表的长度为12,参数值s = 10, t = 30,算法执行的结果。
(2) 说明该算法的功能。
(3) 说明它的渐进时间复杂性。
2、这是一个统计单链表中结点的值等于给定值x的结点数的算法,其中有两处错误,请指出并改正。
int count ( ListNode * Ha, ElemType x ) ①
{ // Ha为不带头结点的单链表的头指针
int n = 0; ②
while ( Ha->link != NULL ) { ③
Ha = Ha->link; ④
if ( Ha->data == x ) n++; ⑤
}
return n; ⑥
}
3、已知二叉树中的结点类型用BinTreeNode表示,被定义为:
struct BinTreeNode
{
ElemType data;
BinTreeNode *leftChild, *rightChild;
};
其中data为结点值域,leftChild和rightChild分别为指向左、右子女结点的指针域。下面函数的功能是从二叉树BT中查找值为x的结点,返回指向其父结点的指针。若该结点不存在或为树根结点则返回空。算法中参数PT的初值为NULL。请在划有横线的地方填写合适的内容。
BinTreeNode *ParentPtr(BinTreeNode *BT, BinTreeNode *PT, ElemType &x)
{
if (BT == NULL)
return NULL;
else if (BT->data == x)
return PT;
else
{
if (PT = ParentPtr(BT->leftChild, BT, x))
_______(1) ________;
________________________(2)
________________________;
else _______(3) ________;
}
}
(1) _____________________________________________
(2) _____________________________________________
(3) _____________________________________________
六、算法设计 (10分)
- 已知二叉树中的结点类型用BinTreeNode表示,被定义为:
struct BinTreeNode
{
char data;
BinTreeNode *leftChild, *rightChild;
};
其中data为结点值域,leftChild和rightChild分别为指向左、右子女结点的指针域,根据下面函数声明编写出删除一棵二叉树中所有结点的算法,并使树根指针为空。假定引用参数BT初始指向这棵二叉树的根结点。
void ClearBinTree ( BinTreeNode*& BT)
// ToDo
## 二、TJP组
### TJP组一
### TJP组二
### TJP组三
## 三、LZH组
### LZH 组一
### LZH 组二
### LZH 组三
### LZH 组四
### LZH 组五
### LZH 组六
### LZH 组七
## 四、LB组
### LB组一
### LB组二
### LB组三
### LB组四
### LB组五
### LB组六
### LB组七
### LB组八