Python整数在底层存储方式
- 1. Python整数在底层对应的结构体 PyLongObject
- 2.整数是怎么存储的
- 2.1 整数0存储
- 2.2 整数1
- 2.3 整数-1
- 2.4. 2**30 -1
- 2.5 . 2**30
- 2.6 . ob_digit[a, b, c] 对应整数计算
- 计算整数所占内存大小
- 总结
Python的底层是C/C++ ,但是 C/C++ 能表示的整数范围是有限的,那么Python 是如何做到:整数不溢出的了?
下面我们从以下几个方面来分析下。
- Python整数在底层对应的结构体 PyLongObject定义
- 整数是怎么存储的
- 整数占的内存大小是怎么计算的
- 两个整数是怎么比较大小
- 整数的加减法运算
1. Python整数在底层对应的结构体 PyLongObject
下面我们来看一下 python3.11 版本源码,它的源码是 C++语言写的
// Include/cpython/longIntrepr.h
struct _longobject {
PyObject _VAR_HEAD
digit ob_digit[1];
}
// Include/pytypedefs.h
typedef struct _longobject PyLongObject
// 那么将两者结合起来
typedef struct {
PyObject _VAR_HEAD
digit ob_digit[1];
}PyLongObject;
// 如果把这个 PyLongObject 更细致的展开一下
typedef struct
{
// 引用计数
Py_ssize_t ob_refcnt;
// 类型
struct _typeobject *ob_type;
// 维护的元素个数
Py_ssize_t ob_size;
// digit 类型的数组
digit ob_digit[1];
}PyLongObjcet
根据上述C++存储代码,我们可以得到如下信息:
- ob_size 指的是 数组 ob_digit 的长度,而 ob_digit 只能用来维护具体的值,而数组长度的不同,那么对应的整数占用内存也就不同。
💚💚💚
我们再来看下: ob_digit 数组的定义
// ob_digit 定义
longintrepr.h
# if PYLONG_BITS_IN_DIGIT =30
typedef unint32_t digit;
#elif PYLONG_BITS_IN_DIGIT =15
typedef unsigned short digit;
#endif
- 由于现在基本都是64位机器,所以只考虑64 位,显然 PYLONG_BITS_IN_DIGIT 会等于30 。 因此 digit 等价于 unint32_t ,也就是 unsigned int ,所以它是一个 无符号32位整型。
- 因此 ob_digit 是一个无符号 32位 整型数组,长度为1 当然这个数据具体多长则取决于你要存储的整数有多大
- 数组的长度具体是多少,取决于你的实际整数,显然整数越大,这个数组就越长,占用的空间也就越大。
2.整数是怎么存储的
下面,我们就以 Python整数的底层存储为例,来详细解释下Python底层存储的原则。
2.1 整数0存储
当表示的整数为0时,ob_digit 数组为空,不存储任何值,而 ob_size为0, 表示这个整数的值为0, 这是一种特殊情况。
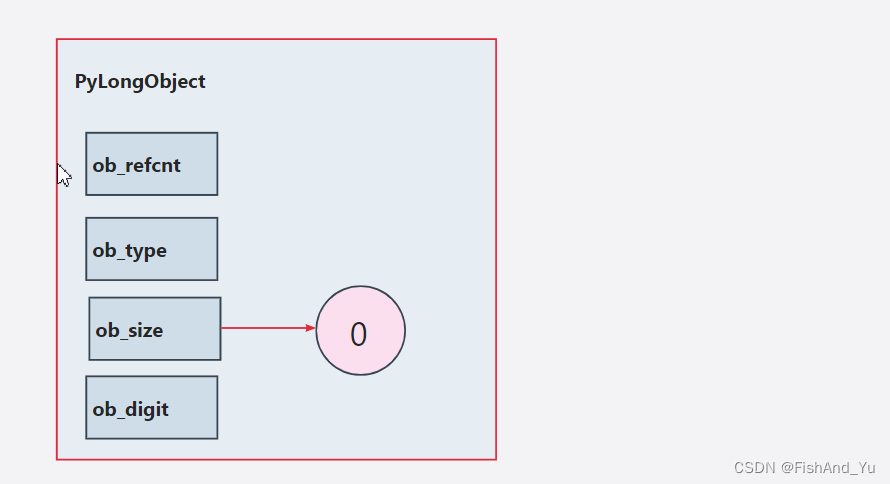
2.2 整数1
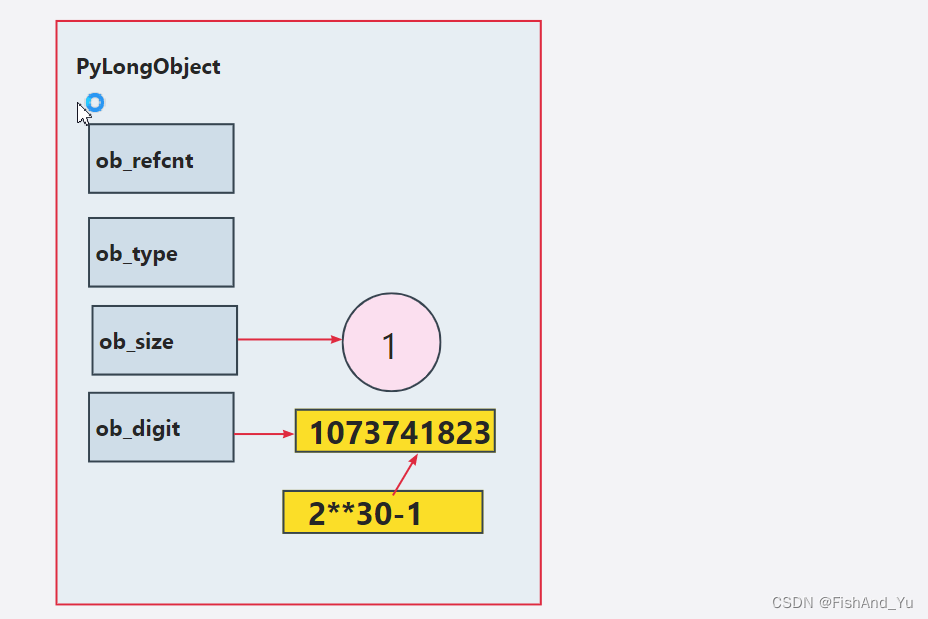
当存储的值为1时,此时 ob_digit 数组就是 [1] ,显然 ob_size 的值也是 1, 因为 它维护的就是 ob_digit 数组的长度。
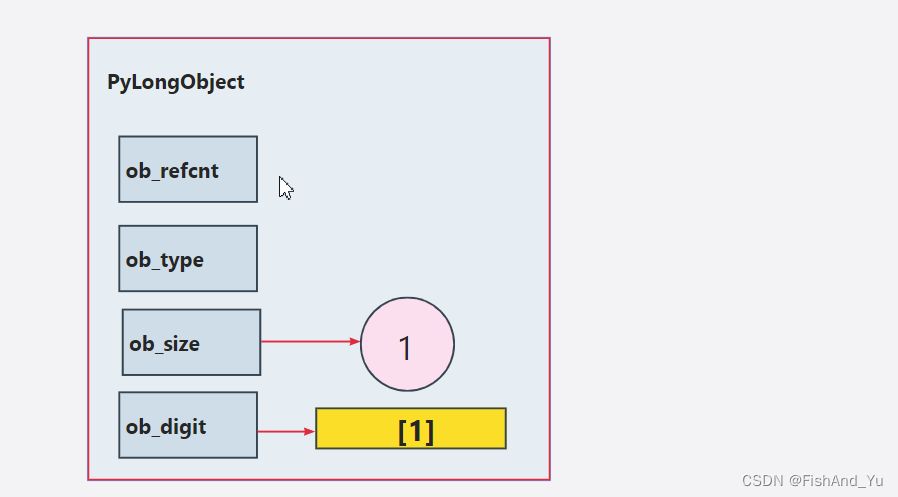
2.3 整数-1
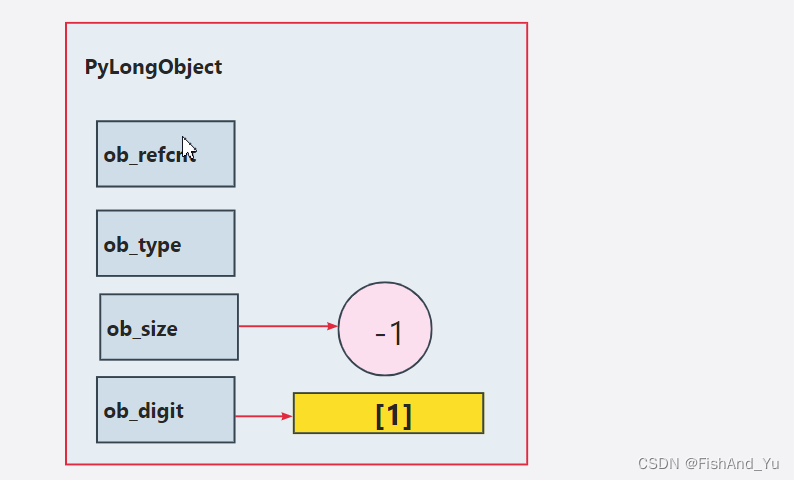
- 我们可以看到 ob_digit 数组没有变化,但是 ob_size长度变为 -1, 整数的正负号就是通过这里的 ob_size来决定的
- ob_digit 存储的其实是绝对值,无论整数 n 是多少 -n和n 对应的 digit 是完全一致的,但是 ob_size 则刚好相反,所以ob_size 除了表示数组的长度之外,还可以表示对应整数的正负。
- 整数越大,底层的数组就越长,更准确的说是绝对值越大,底层数组就越长。
- 所以,Python 在比较两个整数的大小时,会先比较 ob_size ,如果 ob_size 不一样则可以直接比较出大小,显然 ob_size越大,对应的整数越大,不管 ob_size 是正是负,都符合这个结论。
2.4. 2**30 -1
如果想表示:2**30-1 , 我们直接按照前面三个小节,就可以表示这个整数值,但是为什么需要将这个整数单独拿出来说了 ?
💚💚💚
答案就是:虽然 digit 是 4字节32位,但是解释器 只用了 30位
- 如果32个位全部用来存储绝对值,那么相加产生进位的时候,可能会溢出 (如: 2**32-1 此时 32个位全部占满了,即便它只加1,也会溢出),为了解决这个问题:
1:可以先强制转换成 64位整数再进行运算,但是这会以影响效率。
2:但是如果只用30位的话,那么加法就不会溢出。
3:如果数值大到 30个位存不下的话,那么就会多使用一个 digit
2.5 . 2**30
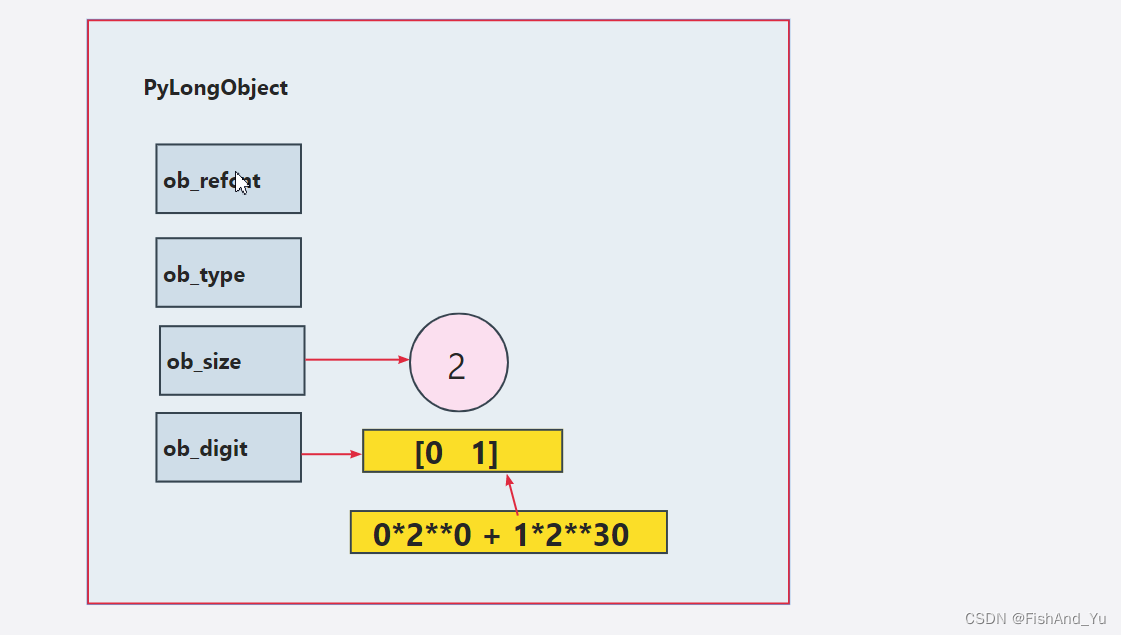
显然 30个位能表达的最大整数是:230-1 ,它是digit 能存的最大值,而现在 是 230 , 所以数组就要有两个 digit
将两个 digit 的值相加 就可以表示 2**30-1 了。
2.6 . ob_digit[a, b, c] 对应整数计算

计算整数所占内存大小
总结
- 因为底层使用数组存储的,而数组的长度又没限制,所以,理论上就不会溢出。
所以,要想支持任意大小的整数运算,首先要找到适合存放整数的方式,本篇介绍了用 int 数组来存放,当然也可以用字符串来存储,找到合适的数据结构后,要重新定义所有运算操作。
💚💚💚 下面这个思想可以好好想想 。
一个 8 位的无符号整数类型,我们知道它能表示的最大数字是 255,但这时候如果我想表示 256,要怎么办?
可能有人会想,那用两个数来存储不就好了。一个存储 255,一个存储 1,将这两个数放在数组里面。这个答案的话,虽然有些接近,但其实还有偏差:那就是我们并不能简单地按照大小拆分,比如 256 拆分成 255 和 1,要是 265 就拆分成 255 和 10,不能这样拆分。
正确的做法是通过二进制的方式,也就是用新的整数来模拟更高的位。
参考 https://www.jb51.net/article/266697.htm