目录
最大堆的建立
方法1
方法2
思路图解
代码实现
代码解释
PercDown
BuildHeap
最大堆的建立
建立最大堆:将已经存在的N个元素按最大堆的要求存放在一个一维数组中。
方法1
通过插入操作,将N个元素一个一个地插入到一个初始为空的堆中去。堆插入的时间复杂度为,插人N个元素,那么最终建立堆的时间复杂度就为
。
方法2
在线性时间复杂度下建立最大堆。
(1)将N个元素按输入顺序存入,先满足完全二叉树的结构特性
(2)调整各结点位置,以满足最大堆的有序性。
我们当然要选择更高效率的方法,下面就来看看方法2具体是怎样实现的:
思路图解
假设现在有12个元素,已经按输入顺序存入,满足了完全二叉树的结构特性:
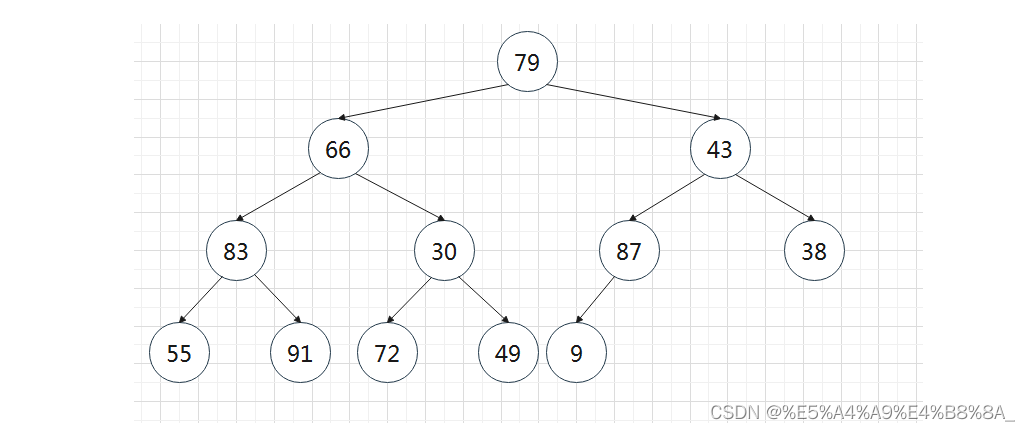
对其进行调整,调整的思路和堆的删除相似,但是要从后往前开始,在左右两个堆中进行调整;我们从倒数第一个有儿子的结点开始调整。因为倒数第一个结点一定是只有左儿子或者有一个左儿子和一个右儿子,即左右两边一定是堆的结构。

调整完倒数第一个有儿子 的结点之后,往上再进行调整。 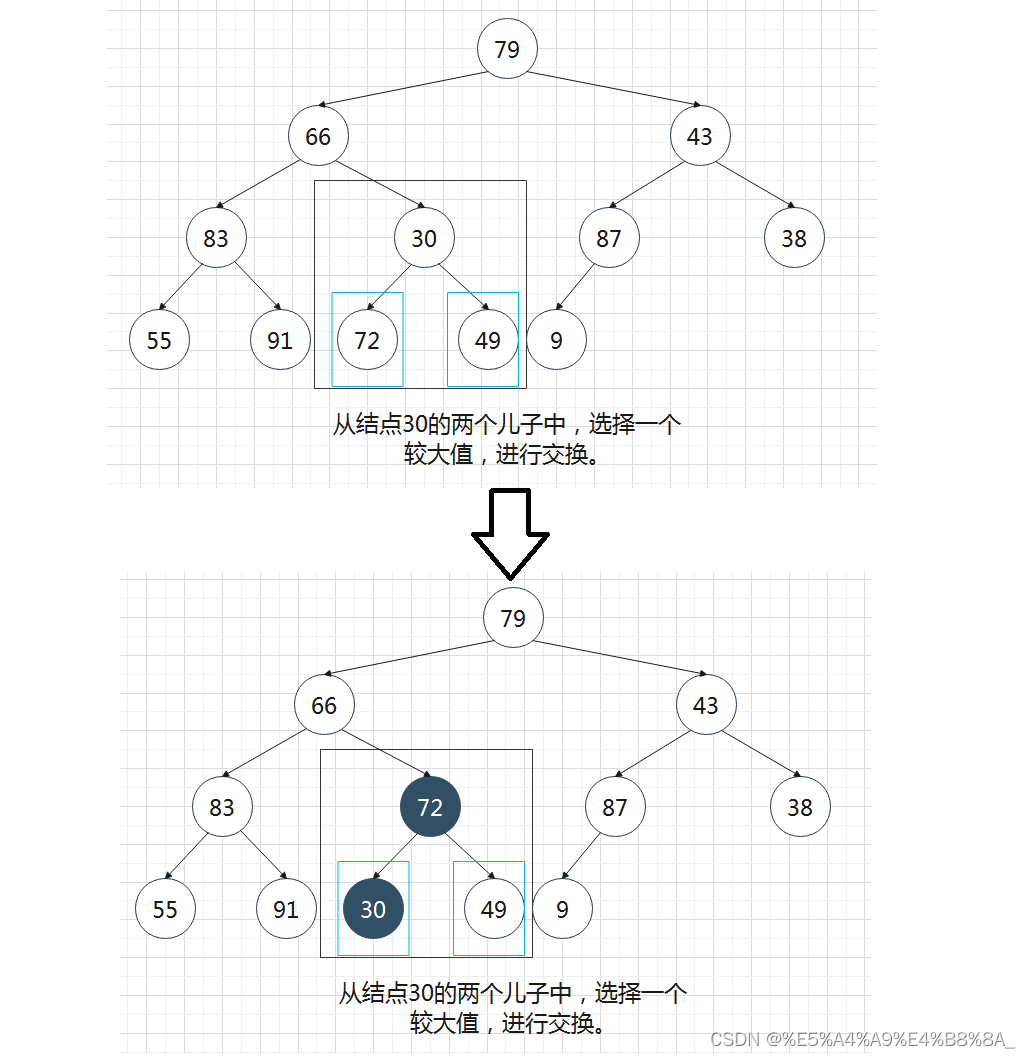
重复操作
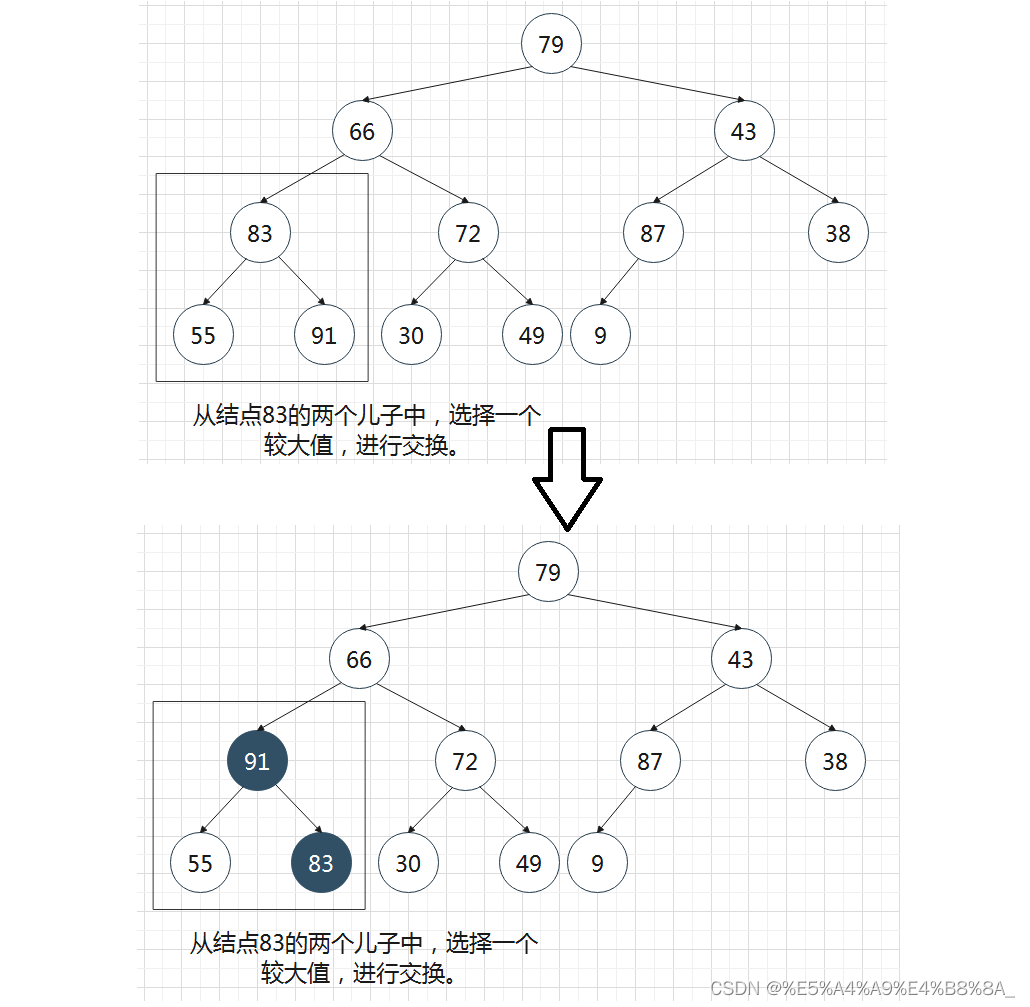
继续往上,到上一层了。 
循环

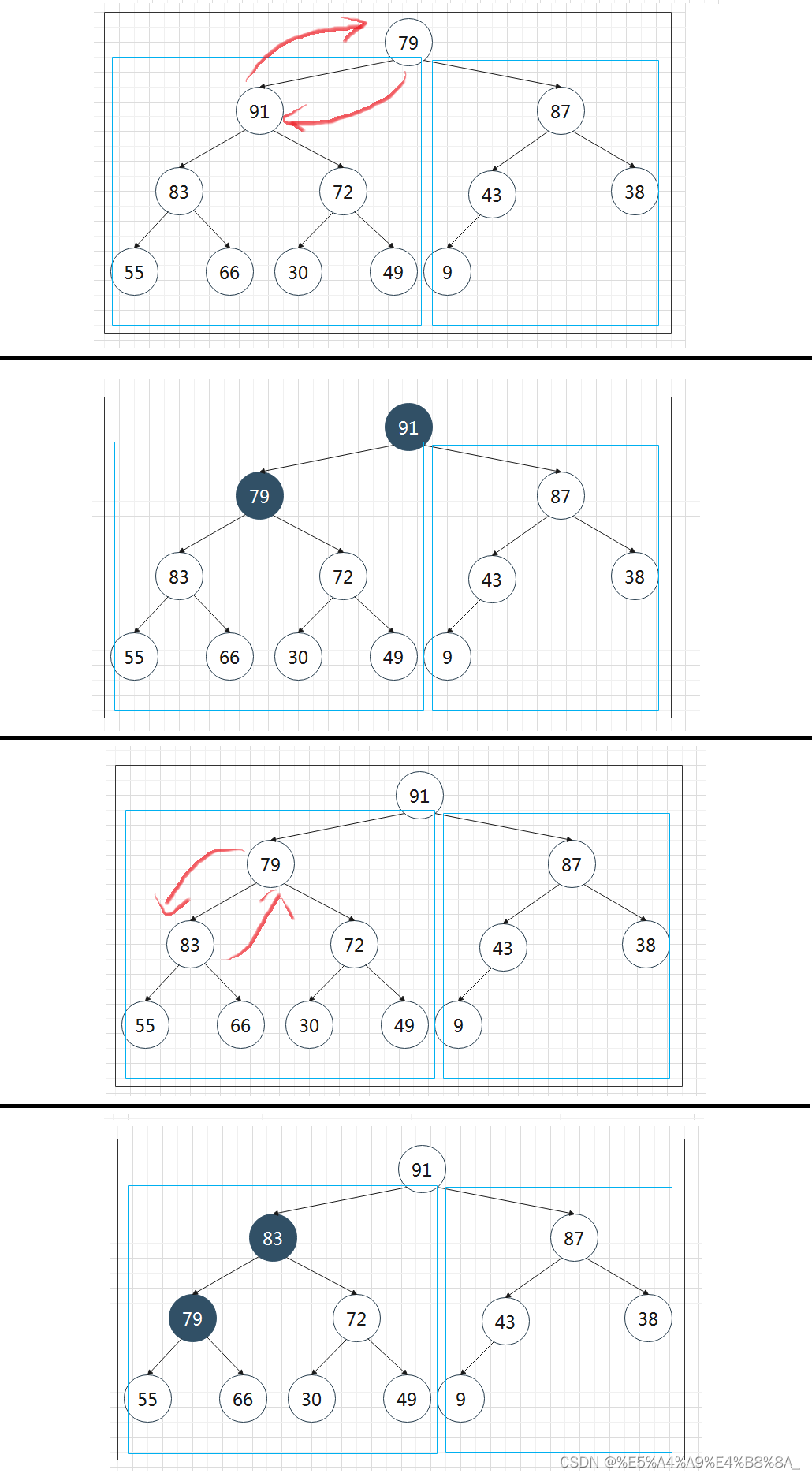
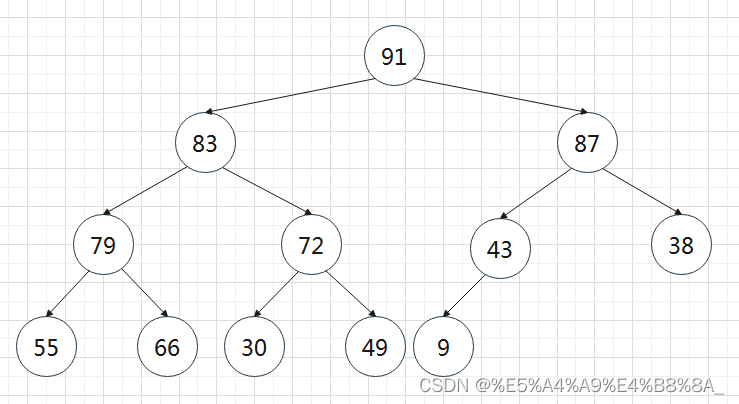
最终调整完成 :
代码实现
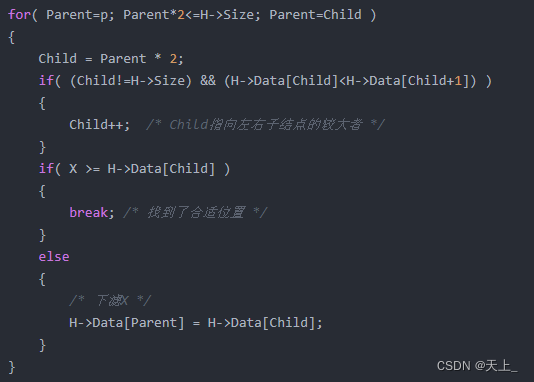
/* 下滤操作:将H中以H->Data[p]为根的子堆调整为最大堆 */
void PercDown( MaxHeap H, int p )
{
int Parent, Child;
ElementType X;
X = H->Data[p]; /* 取出根结点存放的值 */
for( Parent=p; Parent*2<=H->Size; Parent=Child )
{
Child = Parent * 2;
if( (Child!=H->Size) && (H->Data[Child]<H->Data[Child+1]) )
{
Child++; /* Child指向左右子结点的较大者 */
}
if( X >= H->Data[Child] )
{
break; /* 找到了合适位置 */
}
else
{
/* 下滤X */
H->Data[Parent] = H->Data[Child];
}
}
H->Data[Parent] = X;
}
/* 将一个无序的数组调整为最大堆 */
void BuildHeap( MaxHeap H )
{
/* 这里假设所有H->Size个元素已经存在H->Data[]中 */
int i;
/* 从最后一个结点的父节点开始,到根结点1 */
for( i = H->Size/2; i>0; i-- )
PercDown( H, i );
}代码解释
PercDown
PercDown函数用于将以某个结点为根的子树调整为最大堆。
其中,参数p,表示要下滤的结点在H中的下标。
Parent表示当前结点的父结点,Child表示当前结点的子结点,X表示当前结点的值。
![]()
首先,将要下滤的结点的值X取出来,保存在一个临时变量中。
然后,从要下滤的结点开始,沿着其左右子结点中较大的一个不断下滤,
直到找到X的合适位置或者到达叶结点为止。(Child的判断那里与堆的删除那里是一致的)
具体来说,每次将要下滤的结点与其左右子结点中较大的一个进行比较,
如果X比较大,则说明X已经找到了合适的位置,可以退出循环;(最大堆根结点比左右子结点都要大)
否则,将较大的子节点上移一层,继续下滤。
![]()
最后,将X放到找到的合适位置上,完成下滤操作。
BuildHeap
BuildHeap函数用于将一个无序的数组调整为最大堆。

从倒数第一个没有儿子的结点开始,即从最后一个非叶子节点开始,依次进行下滤操作,将其子树调整为最大堆。
因为最后一个非叶子节点的数组下标为n/2,其中n为堆中元素的个数,所以从i=n/2开始循环。
循环执行,直到整个数组都被调整为最大堆。
综上,BuildHeap函数的时间复杂度为,其中N为堆中元素的个数。因为每个结点最多只需要下滤一次,而下滤的时间复杂度为
,所以建立一个最大堆,总的时间复杂度为
。与开头所说相符合,效率较方法1要更高。
end
学习自:MOOC数据结构——陈越、何钦铭



![[JAVA EE]创建Servlet——实现Servlet接口笔记1](https://img-blog.csdnimg.cn/f6f62e6f5a4e407397e969957716efc8.png)