📝个人主页:爱吃炫迈
💌系列专栏:数据结构与算法
🧑💻座右铭:道阻且长,行则将至💗
文章目录
- 二叉树基本概念
- 性质
- 二叉树的种类
- 满二叉树
- 完全二叉树
- 二叉搜索树
- 平衡二叉搜索树
- 二叉树的存储
- 顺序存储
- 链式存储
- 二叉树的遍历
- 前序遍历
- 中序遍历
- 后序遍历
- 层次遍历
- 💞总结💞
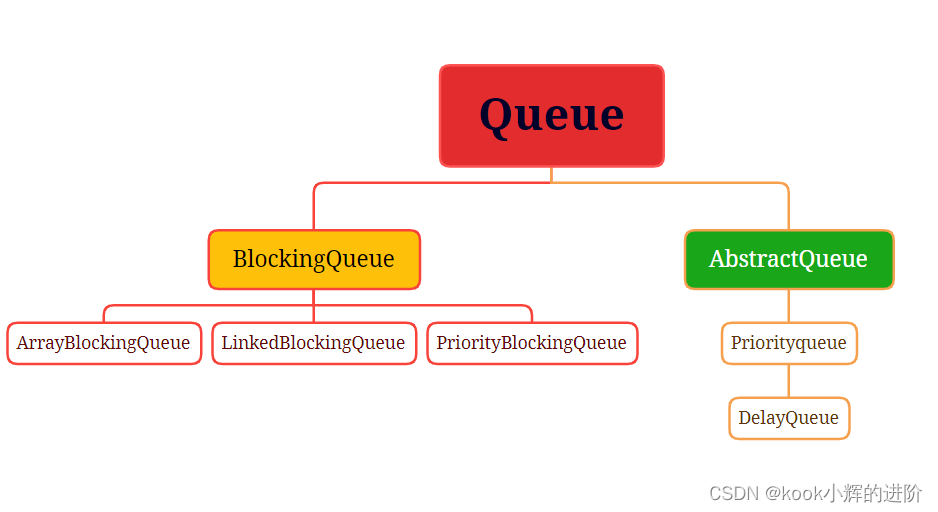
二叉树基本概念
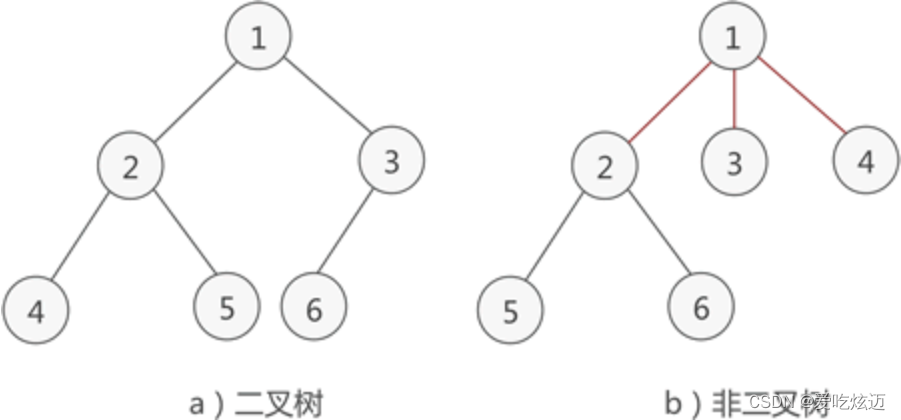
满足两个条件的树就是二叉树:
- 本身是有序树;
- 树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2;
性质
- 二叉树中,第 i 层最多有 2i-1 个结点。
- 如果二叉树的深度为 K,那么此二叉树最多有 2K-1 个结点。
- 二叉树中,终端结点数(叶子结点数)为 n0,度为 2 的结点数为 n2,则 n0=n2+1。
性质 3 的计算方法为:
🌸对于一个二叉树来说,除了度为 0 的叶子结点和度为 2 的结点,剩下的就是度为 1 的结点(设为 n1),那么总结点 n=n0+n1+n2。
🌸同时,对于每一个结点来说都是由其父结点分支表示的,假设树中分枝数为 B,那么总结点数 n=B+1。而分枝数是可以通过 n1 和 n2 表示的,即 B=n1+2n2。所以,n 用另外一种方式表示为 n=n1+2n2+1。
🌸两种方式得到的 n 值组成一个方程组,就可以得出 n0=n2+1。
二叉树的种类
满二叉树
如果二叉树中除了叶子结点,每个结点的度都为 2,则此二叉树称为满二叉树。
如图所示:
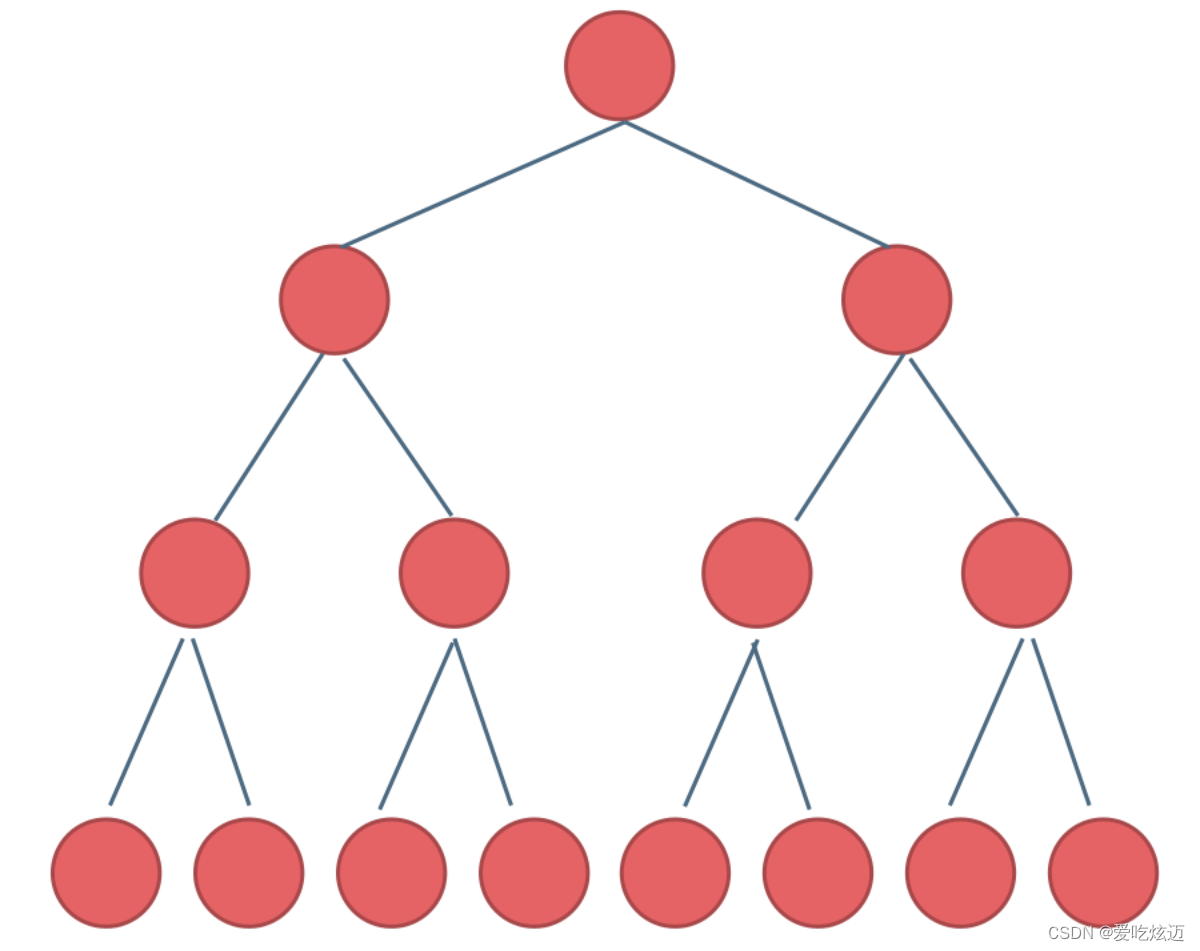
🦕满二叉树除了满足普通二叉树的性质,还具有以下性质:
- 满二叉树中第 i 层的节点数为 2n-1 个。
- 深度为 k 的满二叉树必有 2k-1 个节点 ,叶子数为 2k-1。
- 满二叉树中不存在度为 1 的节点,每一个分支点中都两棵深度相同的子树,且叶子节点都在最底层。
- 具有 n 个节点的满二叉树的深度为 log2(n+1)。
完全二叉树
如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布,则此二叉树被称为完全二叉树
如图所示:
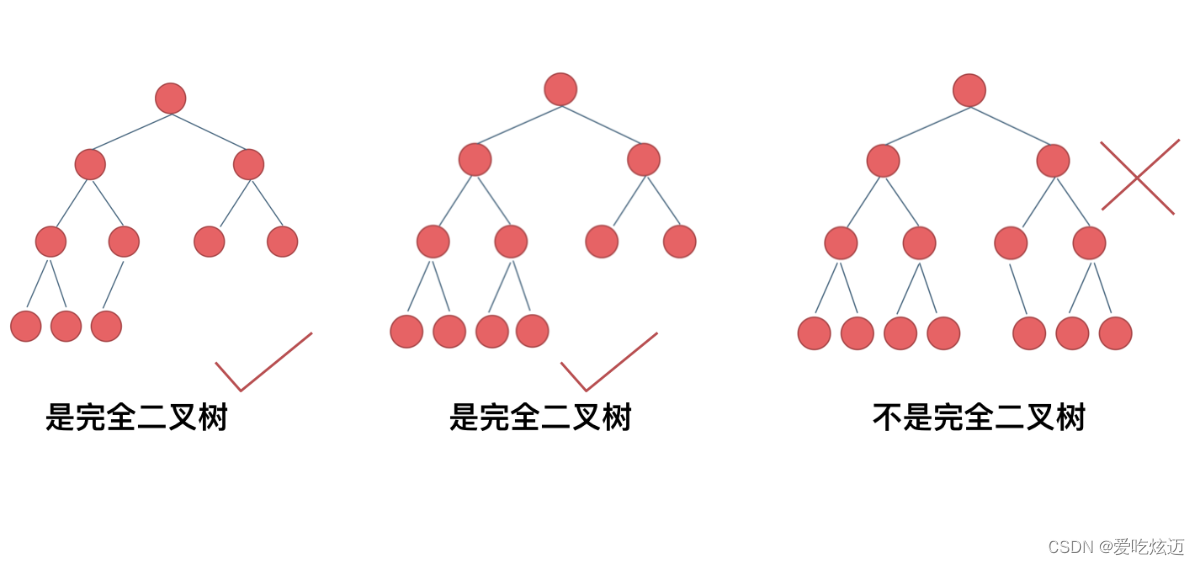
注意:图 3由于最后一层的节点没有按照从左向右分布,因此只能算作是普通的二叉树
🦕完全二叉树除了满足普通二叉树的性质,还具有以下性质:
- n 个结点的完全二叉树的深度为 ⌊log2n⌋+1。
⌊log2n⌋ 表示取小于 log2n 的最大整数。例如,⌊log24⌋ = 2,而 ⌊log25⌋ 结果也是 2。
- 对于任意一个结点 i ,完全二叉树还有以下几个结论成立:
- 当 i>1 时,父亲结点为结点 [i/2] 。(i=1 时,表示的是根结点,无父亲结点)
- 如果 2i>n(总结点的个数) ,则结点 i 肯定没有左孩子(为叶子结点);否则其左孩子是结点 2i 。
- 如果 2i+1>n ,则结点 i 肯定没有右孩子;否则右孩子是结点 2i+1 。
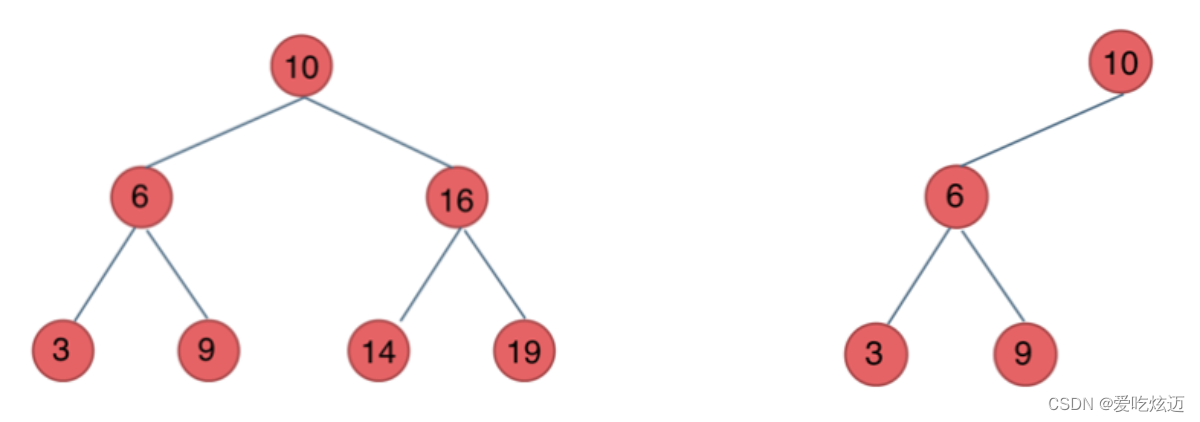
二叉搜索树
前面介绍的树,都没有数值的,而二叉搜索树是有数值的了,二叉搜索树是一个有序树。
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树
如图所示:
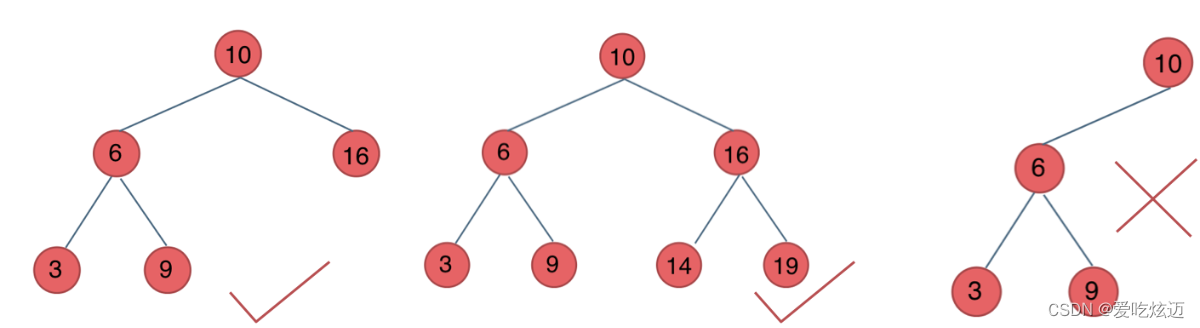
平衡二叉搜索树
平衡二叉搜索树又被称为AVL(Adelson-Velsky and Landis)树
性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
如图所示:
二叉树的存储
顺序存储
从根节点开始,按照层次依次将树中节点存储到数组即可
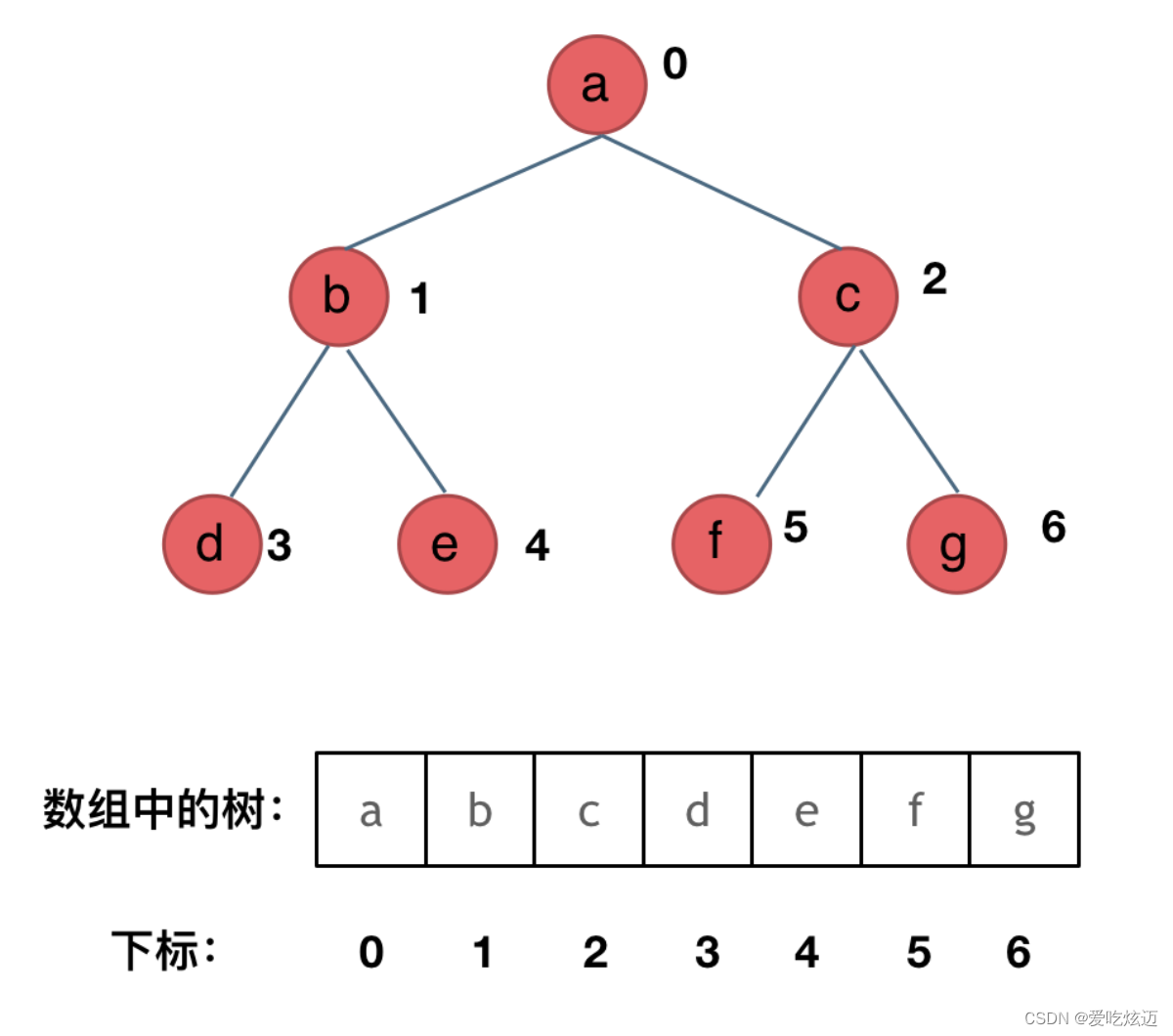
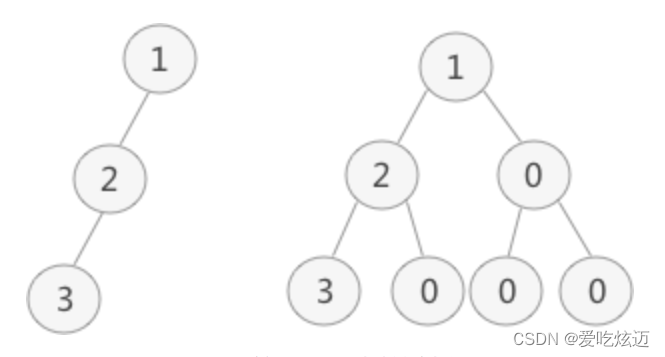
💥需要注意的是,顺序存储只适用于完全二叉树。换句话说,只有完全二叉树才可以使用顺序表存储。因此,如果我们想顺序存储普通二叉树,需要提前将普通二叉树转化为完全二叉树。
💥普通二叉树转完全二叉树的方法很简单,只需给二叉树额外添加一些节点,将其"拼凑"成完全二叉树即可。如图所示:
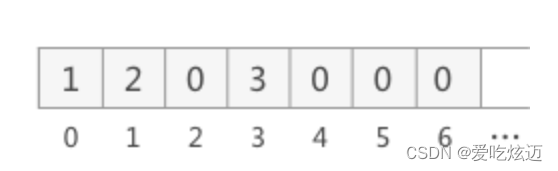
💥普通二叉树的顺序存储:
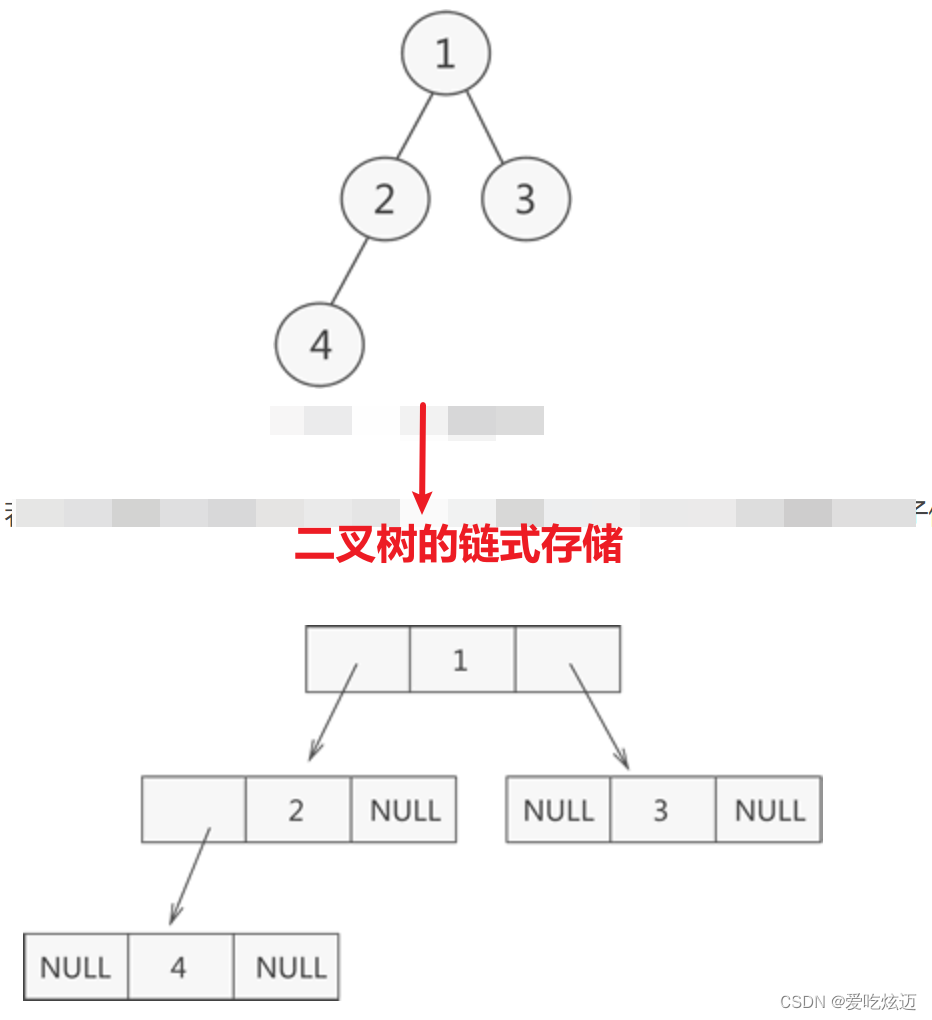
链式存储
从树的根节点开始,将各个节点及其左右孩子使用链表存储即可
采用链式存储二叉树时,其节点结构由 3 部分构成:
- 指向左孩子节点的指针(Lchild)
- 节点存储的数据(data)
- 指向右孩子节点的指针(Rchild)
二叉树的遍历
前序遍历
递归法:
var preorderTraversal = function(root) {
let res=[];
const dfs=function(root){
if(root===null)return ;
//先序遍历所以从父节点开始
res.push(root.val);
//递归左子树
dfs(root.left);
//递归右子树
dfs(root.right);
}
//只使用一个参数 使用闭包进行存储结果
dfs(root);
return res;
};
迭代法:
// 前序遍历:中左右
// 压栈顺序:右左中
var preorderTraversal = function(root, res = []) {
const stack = [];
if (root) stack.push(root);
while(stack.length) {
const node = stack.pop();
if(!node) {
res.push(stack.pop().val);
continue;
}
if (node.right) stack.push(node.right); // 右
if (node.left) stack.push(node.left); // 左
stack.push(node); // 中
stack.push(null);
};
return res;
};
中序遍历
递归法:
var inorderTraversal = function(root) {
let res=[];
const dfs=function(root){
if(root===null){
return ;
}
dfs(root.left);
res.push(root.val);
dfs(root.right);
}
dfs(root);
return res;
};
迭代法:
// 中序遍历:左中右
// 压栈顺序:右中左
var inorderTraversal = function(root, res = []) {
const stack = [];
if (root) stack.push(root);
while(stack.length) {
const node = stack.pop();
if(!node) {
res.push(stack.pop().val);
continue;
}
if (node.right) stack.push(node.right); // 右
stack.push(node); // 中
stack.push(null);
if (node.left) stack.push(node.left); // 左
};
return res;
};
后序遍历
递归法:
var postorderTraversal = function(root) {
let res=[];
const dfs=function(root){
if(root===null){
return ;
}
dfs(root.left);
dfs(root.right);
res.push(root.val);
}
dfs(root);
return res;
};
迭代法:
// 后续遍历:左右中
// 压栈顺序:中右左
var postorderTraversal = function(root, res = []) {
const stack = [];
if (root) stack.push(root);
while(stack.length) {
const node = stack.pop();
if(!node) {
res.push(stack.pop().val);
continue;
}
stack.push(node); // 中
stack.push(null);
if (node.right) stack.push(node.right); // 右
if (node.left) stack.push(node.left); // 左
};
return res;
};
层次遍历
var levelOrder = function(root) {
//二叉树的层序遍历
let res = [], queue = [];
queue.push(root);
if(root === null) {
return res;
}
while(queue.length !== 0) {
// 记录当前层级节点数
let length = queue.length;
//存放每一层的节点
let curLevel = [];
for(let i = 0;i < length; i++) {
let node = queue.shift();
curLevel.push(node.val);
// 存放当前层下一层的节点
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
//把每一层的结果放到结果数组
res.push(curLevel);
}
return res;
};
💞总结💞
希望我的文章能对你学习二叉树有所帮助!