1、pytorch损失函数之nn.BCELoss()（二进制交叉熵)

基础的损失函数 BCE （Binary cross entropy）

1.1 是什么？

这种BCE损失是交叉熵损失的一种特殊情况，因为当你只有两个类时，它可以被简化为一个更简单的函数。这用于测量例如自动编码器中重建的误差。这个公式假设x和y是概率，所以它们严格地在0和1之间。

1.2 怎么代码实现和代码使用？

pytorch中，表示求一个二分类的交叉熵:

class torch.nn.BCELoss(weight=None, size_average=None, reduce=None, reduction=‘elementwise_mean’)

它的loss如下：
l ( x , y ) = L = { l 1 , l 2 , . . . , l n } , 其中 l n = − w n [ y n l o g y n ^ + ( 1 − y n ) l o g ( 1 − y n ^ ) ] l(x,y)=L=\{l_1,l_2,...,l_n\},其中l_n=-w_n[y_nlog\hat{y_n}+(1-y_n)log(1-\hat{y_n})] l(x,y)=L={l1​,l2​,...,ln​},其中ln​=−wn​[yn​logyn​^​+(1−yn​)log(1−yn​^​)]

这里n表示批量大小。 $w_n$​表示权重。

当参数reduce设置为 True，且参数size_average设置为True时，表示对交叉熵求均值，当size_average设置为Flase时，表示对交叉熵求和。参数weight设置的是 $w_n$​，其是一个tensor, 且size与批量数一样(不设置时可能都为1)。目标值 y的范围是0-1之间。输入输出的维度都是 （$（N，\ast ）$，N是批量数，*表示目标值维度。

1.3 推导过程

我们定义：一个二项分布，随机变量只有两种可能值，所以是一个二分类。定义二分类的交叉熵形式：

$$-ylog\hat{y}-(1-y)log(1-\hat{y})..............(1)$$
其中 $\hat{y}$​是输出值在0-1之间.

就是将最后分类层的每个输出节点使用sigmoid激活函数激活，然后对每个输出节点和对应的标签计算交叉熵损失函数，具体图示如下所示：

图片来源：https://www.zhihu.com/question/358811772/answer/920451413

左上角就是对应的输出矩阵（batch_size x num_classes）, 然后经过sigmoid激活后再与绿色标签计算交叉熵损失，计算过程如右方所示。

import torch
import numpy as np

pred = np.array([[-0.4089, -1.2471, 0.5907],
                [-0.4897, -0.8267, -0.7349],
                [0.5241, -0.1246, -0.4751]])
label = np.array([[0, 1, 1],
                  [0, 0, 1],
                  [1, 0, 1]])

pred = torch.from_numpy(pred).float()
label = torch.from_numpy(label).float()

crition1 = torch.nn

输出结果一致，因此训练时使用BCEWithLogitsLoss()和MultiLabelSoftMarginLoss()都可。

分析交叉熵作为损失函数的梯度情况：

我们假设，对于批量样本 $(x_1,y_1),(x_2,y_2)...$则可以对交叉熵求和或者求均值：

$$\sum _i-y_{i}log\widehat{y_i}-(1-y_i)log(1-\widehat{y_i})...........(2)$$
（这里我们将标签值y视作先验分布， $\hat{y}$​为模型分布）

若激活函数使用的是sigmoid函数，则$$\hat{y}=\sigma (z)$$，其中$$z=wx+b$$。采用链式法则求导，则有：

对 $$\frac{1}{n}\sum _i-y_{i}log\widehat{y_i}-(1-y_i)log(1-\widehat{y_i})..........(2)$$

求导，可得：
$$\frac{\partial L}{\partial w}=-\frac{1}{n}\sum _i(\frac{y}{\sigma (z)}-\frac{1-y}{1-\sigma (z)})\frac{\partial \sigma }{\partial w}=-\frac{1}{n}\sum _i(\frac{y}{\sigma (z)}-\frac{1-y}{1-\sigma (z)}){\sigma }^{\prime }x$$

由于 $$\sigma (z)=1/(1+e^{-z})$$

所以最终得到： $$\frac{\partial L}{\partial w}=\frac{1}{n}\sum _{i}x(\sigma (z)-y)$$

而对偏置的导数也等于 $$\frac{\partial L}{\partial b}=\frac{1}{n}\sum _i(\sigma (z)-y)$$可以看见使用交叉熵作为损失函数后，反向传播的梯度不在于sigmoid函数的导数有关了。这就从一定程度上避免了梯度消失。

举一个sigmoid导致的梯度消失的MSE损失的例子

二次函数为损失函数的梯度情况,梯度消失问题

二次函数$$L=\frac{(y-\hat{y}{)}^2}{2}$$

采用链式法则求导，则有：

$$\frac{\partial L}{\partial w}=(\hat{y}-y){\sigma (z)}^{\prime }x$$
$$\frac{\partial L}{\partial b}=(\hat{y}-y){\sigma (z)}^{\prime }$$
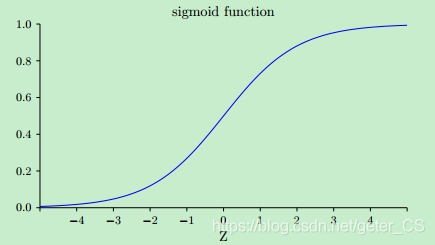
可以看出梯度都与sigmoid函数的梯度有关，如下图所示，sigmoid函数在两端的梯度均接近0，这导致反向传播的梯度也很小，这就这就不利于网络训练，这就是 梯度消失问题 。

1.3 应用场景

在机器学习或者深度学习中，分类问题是一个最常见的任务，分类问题一般又分为：二分类任务、多分类任务和多标签分类任务

• 二分类任务：输出只有0和1两个类别；
• 多分类任务：一般指的是输出只有一个标签，类别之间是互斥的关系；
• 多标签分类任务：输出的结果是多标签，类别之间可能互斥也可能有依赖、包含等关系。

在面对不同的分类问题的时候，选择的loss function也不一样，二分类和多标签分类通常使用sigmoid函数而多分类则一般使用softmax函数（互斥性质）。

1.3.1 二分类

BCE可以处理二分类问题，而且通常是sigmoid+BCELoss。

This loss is a special case of cross entropy for when you have only two classes so it can be reduced to a simpler function. This is used for measuring the error of a reconstruction in, for example, an auto-encoder. This formula assume xx and yy are probabilities, so they are strictly between 0 and 1.

1.3.2 多分类

若是遇到多分类问题使用二进制交叉熵。
目标：多分类问题 => 多个二分类问题

比如我们有3个类别，那么我们通过softmax得到 $$\hat{y}=[0.2,0.5,0.3]$$的到的一个一个样本的分类结果，这个结果的通俗解释就是：为第一类的概率为0.2，为第二类的概率为0.5,为第三类的结果过0.3。
假设这个样本真实类别为第二类，那么我们希望模型输出的结果过应该是$$y=[0,1,0]$$，这个就是标签值。那么损失函数可以使用交叉熵：

$$L=-\sum _k^3{y}_{k}log(\hat{y})$$，

可以看见实际上这个求和只有一项。也就是 $$L=-log(0.5)$$。

pytorch中提供了多分类使用的损失函数nn.CrossEntropyLoss()使用的原理，与这里类似。

作者：杨夕
链接：https://www.zhihu.com/question/358811772/answer/2677137156
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

class BCELosswithLogits(nn.Module):
      def __init__(self, pos_weight=1, reduction='mean'):
          super(BCELosswithLogits, self).__init__()
          self.pos_weight = pos_weight
          self.reduction = reduction

      def forward(self, logits, target):
          # logits: [N, *], target: [N, *]
          logits = F.sigmoid(logits)
          loss = - self.pos_weight * target * torch.log(logits) - \
                (1 - target) * torch.log(1 - logits)
          if self.reduction == 'mean':
              loss = loss.mean()
          elif self.reduction == 'sum':
              loss = loss.sum()
          return loss

存在问题：由于 head classes的主导以及negative instances的影响，导致 BCE Loss 函数 容易受到 类别不均衡问题 影响；

优化方向：绝大部分balancing方法都是reweight BCE从而使得稀有的instance-label对能够得到得到合理的“关注”

1.3.3 位置的回归

使用中心位置使用BCE是有理论依据的，可以认为，效果等价于square L2 norm（这个结论的出处还没找到，等找到了补充，20230506）

1.3.4 用途的一个示例

2、BCEWithLogitsLoss

nn.BCEWithLogitsLoss() 函数等效于 sigmoid + nn.BCELoss。

BCEWithLogitsLoss损失函数把 Sigmoid 层集成到了 BCELoss 类中. 该版比用一个简单的 Sigmoid 层和 BCELoss 在数值上更稳定, 因为把这两个操作合并为一个层之后, 可以利用 log-sum-exp 的 技巧来实现数值稳定.

torch.nn.BCEWithLogitsLoss(weight=None, reduction='mean', pos_weight=None)

参数：

    weight (Tensor, optional) – 自定义的每个 batch 元素的 loss 的权重. 必须是一个长度 为 “nbatch” 的 Tensor

参考

https://atcold.github.io/pytorch-Deep-Learning/en/week11/11-1/
https://mp.weixin.qq.com/s/AwgQcafQ2pAuU7_0gEFnmg
https://pytorch-cn.readthedocs.io/zh/latest/package_references/torch-nn/#normalization-layers-source
https://samuel92.blog.csdn.net/article/details/105900876
https://blog.csdn.net/geter_CS/article/details/84747670