第一范式(1NF):每一列都是不可分割的原子数据项(什么意思,每一项都不可分割,像下面的表格就能分割,所以它连第一范式都算不上)
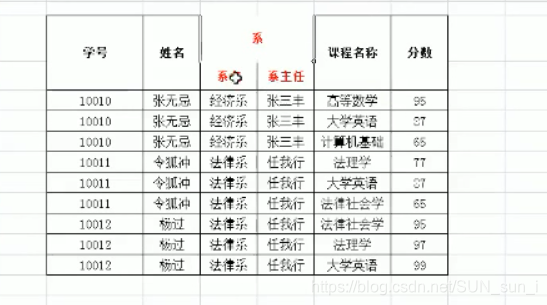
分割后的样子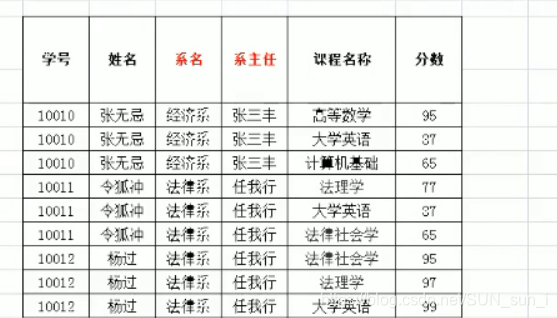
(它就是第一范式了)
第二范式:在1NF基础上,非码属性必须完全依赖于候选码(在1NF基础上消除非主属性对主码的部分函数依赖)
几个重要的概念:
1.函数依赖:A–>B,如果通过A属性(属性组)的值,可以确定唯一的B属性的值,则称B依赖于A
例如:学号---->姓名 (学号、课程名称 的属性组)–> 分数
2.完全函数依赖:A–>B 如果A是一个属性组,则B属性值的确定需要依赖A属性组的中所有的属性值
例如:(学号、课程名称)–> 分数
3. 部分函数依赖: A–>B 如果A是一个属性组,则B属性值的确定只需要依赖A属性组的中某一些的属性值(第二范式就是消除这个)
例如:(学号 、课程名称)–> 姓名
4.传递函数依赖:A – >B , B – >C 如果通过A属性(属性组)的值,可以确定唯一的B属性的值,再通过B属性(属性组)的值,可以唯一确定C属性的值,那么称C传递依赖于A
例如: 学号 --> 系名 ,系名 --> 系主任
5.码 :如果在一张表中,一个属性或属性组,被其他所有的属性(非主属性)所完全函数依赖,则称这个属性(属性组)为该表的码。(上面的表,学号和课程名称所构成的属性组就是码)
例如: 该表中码为 (学号、课程名称)
主属性: 码中所有属性
非主属性: 除码之外的所有属性
在上面那张表中我们可知码为(学号、课程名称),但是姓名、系名、系主任都部分依赖于码(主属性),这不符合第二范式,所以进行拆分如下
第一张表码为(学号、课程名称),第二张表为(学号),它们都是完全依赖的,因此符合第二范式。
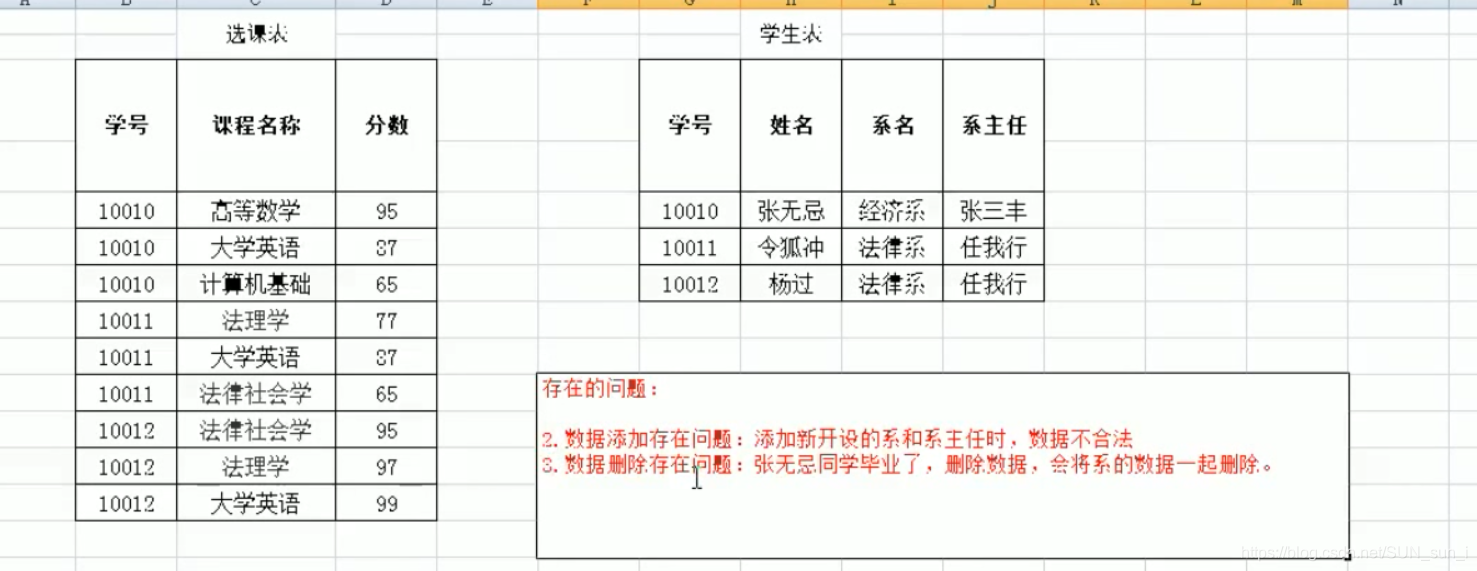
第三范式(3NF):在2NF的基础上,任何的非主属性不依赖于其他非主属性 (在第二范式基础上消除传递依赖)
注意看第二范式的学生表:存在系主任依赖于系名 (系名—> 系主任),所以不符合第三范式
继续进行拆分
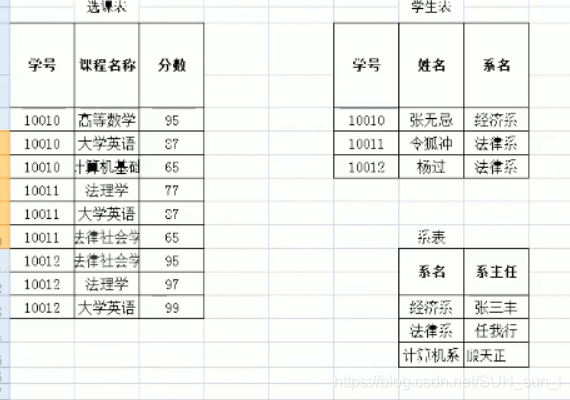
这样就符合第三范式…