1.引入

特指有序、整数的离散化。

离散化，本质上是一种哈希，它在保持原序列大小关系的前提下把其映射成正整数。它可以有效的降低时间复杂度。离散化可以改进一个低效的算法，甚至实现根本不可能实现的算法。

当原数据很大或含有负数、小数时，难以表示为数组下标，一些算法和数据结构无法运作，这时我们就考虑将其离散化。

基本思想就是在众多可能的情况中，只考虑需要用的值，比如给你 $10^9$ 个数，但你只用到 $10^5$ 个数，这时候就可以使用离散化，把这 $10^5$ 个数映射成从0开始的自然数，即数组下标（把稀疏的数据变的稠密起来）。

2.思路

思路是：先排序，再删除重复元素，最后就是索引元素离散化后对应的值。

模板如下

vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end());   // 去掉重复元素

// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1; // 映射到1, 2, ...n
}

离散化可以用STL较简单地完成。

unique 的作用是“去掉”容器中相邻元素的重复元素，这里所说的“去掉”并不是真正把重复元素删除，它实质上是一个伪去除，是把重复的元素移到后面去了，然后依然保存到了原数组中，然后返回去重后最后一个元素的地址。
因为unique去除的是相邻元素的重复元素，所以使用之前需要排序。

注意：① a中可能有重复元素，需要去重（erase,unique）
② 算出a[i]离散化后的值，需要使用二分思想
③离散化的本质，是映射，将间隔很大的点，映射到相邻的数组元素中。减少对空间的需求，也减少计算量。

3.模板题

题目 802. 区间和 - AcWing题库

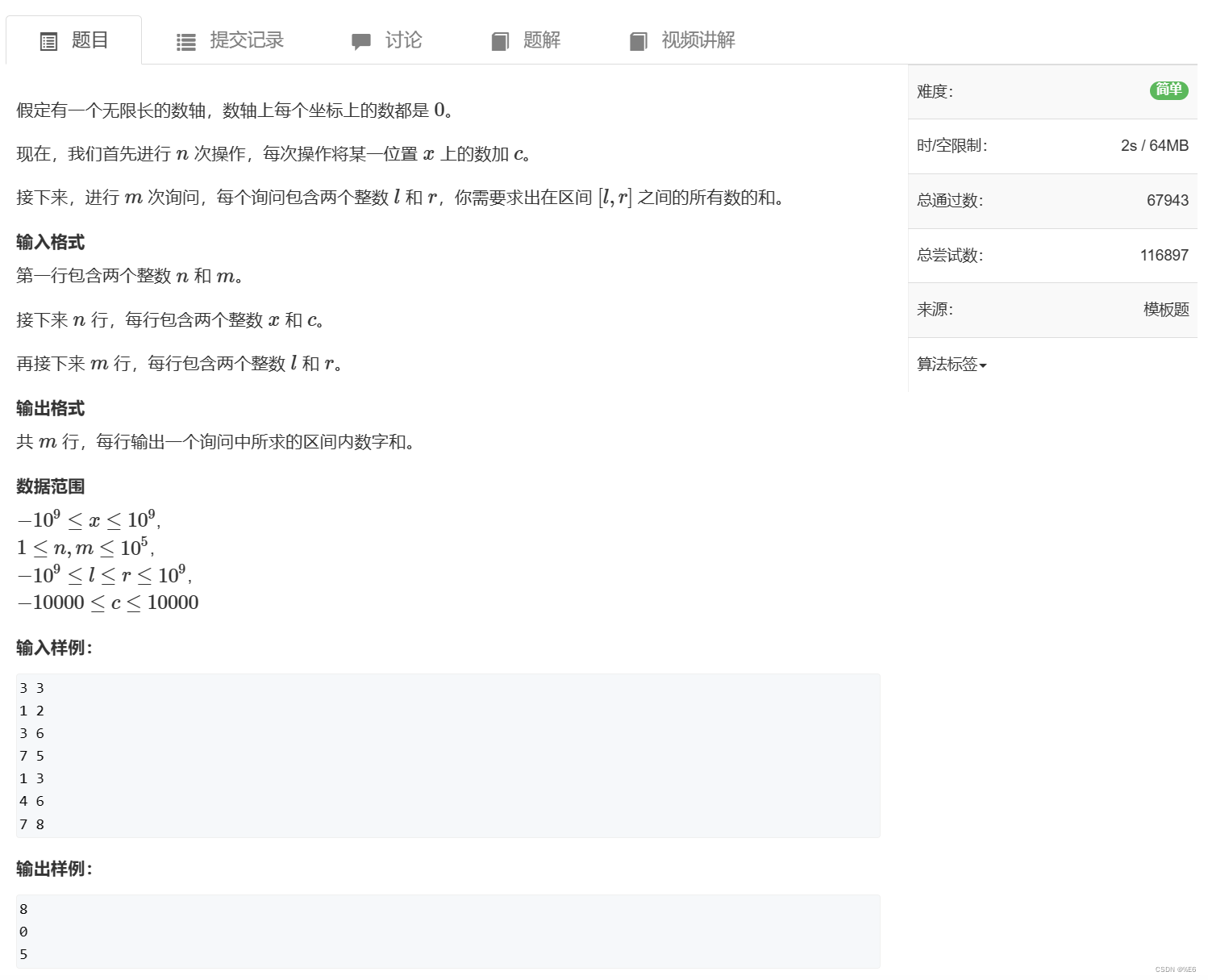
在这里插入图片描述

分析过程

转载链接： AcWing 802. 画个图辅助理解~ - AcWing

代码实现

#include<bits/stdc++.h>
using namespace std;

const int N=3*1e5+10;

typedef pair<int,int> PII;

int n,m;
int a[N]; //存的数
int s[N]; //前缀和

//离散化数组
vector<int> alls;
// add存所有插入操作，query存所有查询操作
// 因为要在离散化之后再处理这些操作，所以它们都要记录下来
vector<PII> add,query;

int find(int x) //求离散化之后的值
{
    int l=0,r=alls.size()-1;
    while(l<r)
    {
        int mid=l+r>>1;
        if(alls[mid]>=x) r=mid;
        else l=mid+1;
    }
    return r+1; //映射的结果是1，2，3...，因为用到前缀和
}

int main()
{
    cin>>n>>m;
    
    for(int i=0;i<n;i++)
    {
       int x,c;
       cin>>x>>c;
       add.push_back({x,c}); //读入所有的操作
       
       alls.push_back(x); 
    }
    
    for(int i=0;i<m;i++)
    {
        int l,r;
        cin>>l>>r;
        query.push_back({l,r});
        
        alls.push_back(l);
        alls.push_back(r); //把所有需要用到的下标放到alls里面去
    }
    
    //去重
    sort(alls.begin(),alls.end());  //按照有序，从小到大
    alls.erase(unique(alls.begin(),alls.end()),alls.end());
    
    //处理加数
    for(auto item : add)
    {
        int x=find(item.first);  //这里可以直接使用 离散化之后的值，因为有序
        a[x]+=item.second;
    }
    
    //预处理前缀和
    for(int i=1;i<=alls.size();i++)
        s[i]=s[i-1]+a[i];
        
    //处理询问
    for(auto item:query)
    {
        int l=find(item.first),r=find(item.second);
        cout<<s[r]-s[l-1]<<endl;
    }
    
    return 0;
}