一、单仓库多旅行商问题
单仓库多旅行商问题(Single-Depot Multiple Travelling Salesman Problem, SD-MTSP):𝑚个推销员从同一座中心城市出发,访问其中一定数量的城市并且每座城市只能被某一个推销员访问一次,最后返回到中心城市,通常这种问题模型被称之为SD-MTSP。
多旅行商问题(Multiple Traveling Salesman Problem, MTSP):单仓库多旅行商问题及多仓库多旅行商问题(含动态视频)_IT猿手的博客-CSDN博客
二、斑马优化算法ZOA求解SDMTSP
斑马优化算法ZOA求解单仓库多旅行商问题,本文选取国际通用的TSP实例库TSPLIB中的测试集bayg29。
2.1部分代码(可更改起点及旅行商个数)
%完整MATLABcode link: https://mbd.pub/o/bread/mbd-ZJiTl5ts
close all
clear
clc
%数据集参考文献 REINELT G.TSPLIB-a traveling salesman problem[J].ORSA Journal on Computing,1991,3(4):267-384.
global data StartPoint Tnum
% 导入TSP数据集 bayg29
load('data.txt')
Tnum=4;%旅行商个数(可以自行更改)2-6
StartPoint=13; %选择起点城市(可以自行更改)
Dim=size(data,1)-1;%维度
lb=-100;%下界
ub=100;%上界
fobj=@Fun;%计算总距离
SearchAgents_no=100; % 种群大小(可以修改)
Max_iteration=5000; % 最大迭代次数(可以修改)
[fMin,bestX,curve]=ZOA(SearchAgents_no,Max_iteration,lb,ub,Dim,fobj); %蜣螂优化算法
%% 最终的结果 Kd是最终的城市序列
[~,idx]=sort(bestX);
idx(idx>=StartPoint)=idx(idx>=StartPoint)+1;
num=floor(length(idx)/Tnum);
Lnum=num*ones(1,Tnum);
Lnum(Tnum)=length(idx)-(Tnum-1)*num;
Kd=StartPoint*ones(Tnum,max(Lnum)+2);
st=1;%起始位置
for i=1:Tnum
en=st+Lnum(i)-1;%结束位置
Kd(i,2:Lnum(i)+1)=idx(st:en);
st=en+1;
end
%% %%%%%%%%%%%%%%%%%%% 保存数据 %%%%%%%%%%%%%%%%%%%%%
save Kd Kd %保留最终的城市序列
save curve curve %保留算法求解的收敛曲线
%% 求解结果画图
PlotResult;%求解结果画图2.2部分结果
(1)4个旅行商

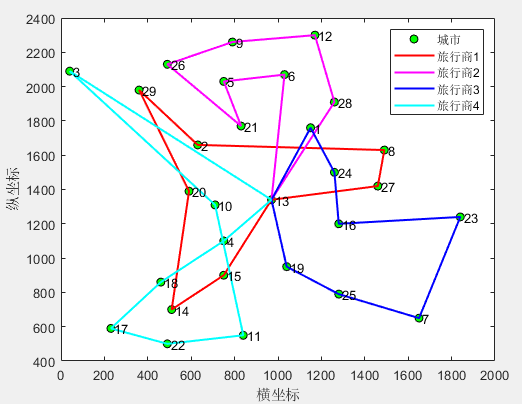
第1个旅行商的路径:13->27->8->2->29->20->14->15->13
第1个旅行商的总路径长度:1558.974022
第2个旅行商的路径:13->6->5->21->26->9->12->28->13
第2个旅行商的总路径长度:1325.820501
第3个旅行商的路径:13->1->24->16->23->7->25->19->13
第3个旅行商的总路径长度:1214.495780
第4个旅行商的路径:13->4->18->17->22->11->10->3->13
第4个旅行商的总路径长度:1911.386931
所有旅行商的总路径长度:6010.677233
(2)3个旅行商
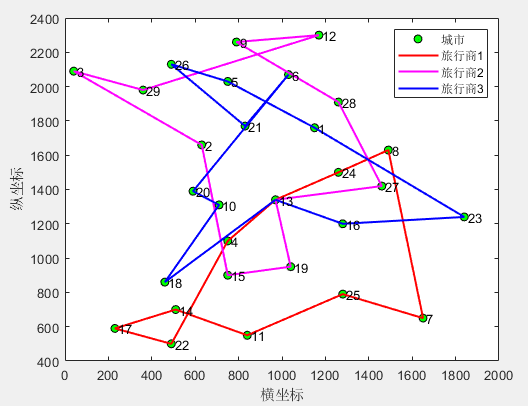
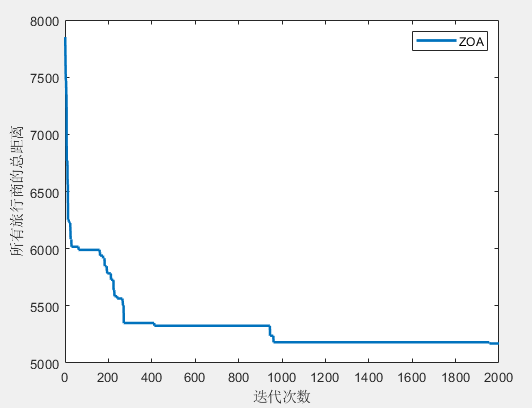
第1个旅行商的路径:13->4->22->17->14->11->25->7->8->24->13
第1个旅行商的总路径长度:1550.612782
第2个旅行商的路径:13->19->15->2->3->29->12->9->28->27->13
第2个旅行商的总路径长度:1804.882268
第3个旅行商的路径:13->18->10->20->6->21->26->5->1->23->16->13
第3个旅行商的总路径长度:1815.323663
所有旅行商的总路径长度:5170.818712