1 Introduction
任务:第三章使用动态规划方法,解决known的MDP问题,这章通过model free prediction对一个unknown的MDP估计他的value function。下一章通过Model free control的方法针对一个unknown的MDP optimise value function。
2 Monte Carlo Learning
2.1 MC 方法的特点
- learn directly from episodes of experiences
- model free: no knowledge of MDP transitions / rewards
- learn from complete episodes: no bootstrapping
- simplest idea: value = mean return
- Caveat: can only apply MC to episodic MDPs
- all episodes must terminate
2.2 MC policy evaluation

##伪代码
1初始化:
- 设定状态集合 S 和动作集合 A
- 定义策略 π
- 设定折扣因子 γ
- 初始化每个状态 s 的价值函数 V(s) 为 0
- 初始化每个状态 s 的回报列表 returns(s) 为空列表
2对于每个情节(episode):
- 初始化状态 s 为初始状态
- 初始化轨迹 trajectory 为空列表
- 当 s 不是终止状态时:
- 按照策略 π 选择动作 a
- 执行动作 a,得到下一个状态 s’ 和奖励 r
- 将 (s, r) 添加到轨迹 trajectory
- 更新状态 s 为 s’
- 初始化累积回报 G 为 0
- 从轨迹的末尾开始向前遍历每个时刻 (s, r):
- 更新累积回报 G = r + γ * G
- 将 G 添加到 returns(s) 列表
- 更新价值函数 V(s) 为 returns(s) 列表的平均值
3 输出价值函数 V
考虑一个简化的冰冻湖环境,其中有四个状态(S, F, H, G),分别表示起点、冰面、洞口和终点。在每个时间步,智能体可以选择左或右2个动作。我们要评估一个简单的策略:始终向右移动
import numpy as np
import random
# 环境参数
states = ["S", "F", "H", "G"]
n_states = len(states)
actions = ["left", "right"]
n_actions = len(actions)
# 策略
policy = np.zeros((n_states, n_actions))
policy[:, actions.index("right")] = 1
# 模拟函数
def step(state, action):
if state == 0 and action == "right":
return 1, 0
if state == 1 and action == "right":
return 2, 0
if state == 1 and action == "left":
return 0, 0
if state == 2 and action == "right":
return 3, 1
if state == 2 and action == "left":
return 1, 0
return state, 0
# 参数
num_episodes = 5000
gamma = 0.99
# 初始化
returns = {state: [] for state in range(n_states)}
v = np.zeros(n_states)
# Monte Carlo Policy Evaluation
for episode in range(num_episodes):
state = 0
episode_trajectory = []
while state != n_states - 1:
action = np.random.choice(actions, p=policy[state, :])
next_state, reward = step(state, action)
episode_trajectory.append((state, reward))
state = next_state
g = 0
for t in range(len(episode_trajectory) - 1, -1, -1):
state, reward = episode_trajectory[t]
g = reward + gamma * g
returns[state].append(g)
v[state] = np.mean(returns[state])
print("Value function:", v)
关键的概念:
- episode
一个情节是指从初始状态到终止状态的一系列状态-动作-奖励的序列 - episode trajectory
在一个情节下,智能体与环境交互过程中,包含的一系列状态和相应的奖励;
这个状态和相应的奖励序列取决于智能体采用什么样的策略,以及环境如何响应这些动作; - 更新累计回报
G t = R t + 1 + γ R t + 2 + . . . + γ R t + 2 T − 1 R T v π ( s ) = E π [ G t ∣ S t = s ] \begin{aligned} G_t &= R_{t+1}+ \gamma R_{t+2}+...+ \gamma R_{t+2}^{T-1}R_T \\ v_{\pi}(s) & = E_{\pi}[G_t|S_t=s] \end{aligned} Gtvπ(s)=Rt+1+γRt+2+...+γRt+2T−1RT=Eπ[Gt∣St=s] - 对比known MDP和MC
#计算reward,MC
while state != n_states - 1:
action = np.random.choice(actions, p=policy[state, :])
next_state, reward = step(state, action)
episode_trajectory.append((state, reward))
state = next_state
g = 0
for t in range(len(episode_trajectory) - 1, -1, -1):
state, reward = episode_trajectory[t]
g = reward + gamma * g
returns[state].append(g)
v[state] = np.mean(returns[state])
#计算reward, DP
# Policy Evaluation
V = np.zeros(n_states)
while True:
delta = 0
for state in range(n_states):
v = V[state]
V[state] = np.sum(policy[state, :] * (rewards[state, :] + gamma * transition_matrix[state, :, :] @ V))
delta = max(delta, abs(v - V[state]))
if delta < theta:
break
2.2 incremental mean
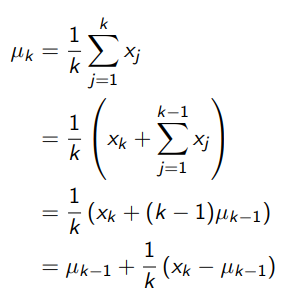
2.3 incremental MC updates
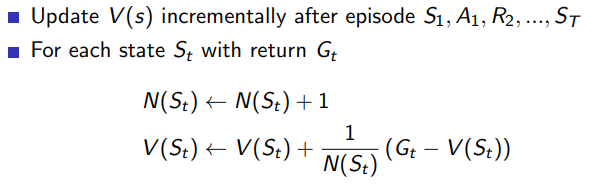
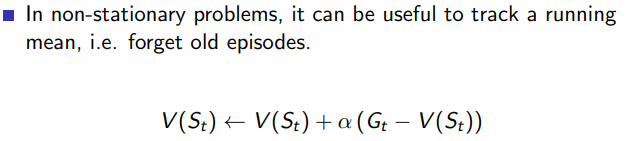
3 Temporal Difference Learning
3.1 TD methods的特点
- TD methods learn directly from episodes of experience
- TD is model free: no knowledge of MDP transitions / rewards
- TD learns from incomplete episodes, by bootstrapping
- TD updates a guess towards a guess
3.2 MC 和TD

用MC解决driving home 的问题
import numpy as np
def generate_episode(policy, n_states, step):
state = 0
episode_trajectory = []
while state != n_states - 1:
action = np.random.choice(actions, p=policy[state, :])
next_state, reward = step(state, action)
episode_trajectory.append((state, reward))
state = next_state
return episode_trajectory
def monte_carlo_policy_evaluation(policy, n_states, n_episodes, step, gamma=1.0):
returns_sum = np.zeros(n_states)
returns_count = np.zeros(n_states)
for episode_idx in range(n_episodes):
episode_trajectory = generate_episode(policy, n_states, step)
G = 0
for t in range(len(episode_trajectory) - 1, -1, -1):
state, reward = episode_trajectory[t]
G = gamma * G + reward
if state not in [x[0] for x in episode_trajectory[:t]]:
returns_sum[state] += G
returns_count[state] += 1
value_function = returns_sum / returns_count
return value_function
# Define the step function for the "Driving Home" problem
def step(state, action):
next_state = state + (1 if action == 1 else -1)
next_state = max(0, min(next_state, n_states - 1)) # Make sure we stay within the state bounds
reward = -1
if next_state == n_states - 1:
reward = 0
return next_state, reward
# Define the environment's parameters
n_states = 5
n_actions = 2
actions = np.arange(n_actions)
# Define the initial policy (random policy in this case)
policy = np.ones((n_states, n_actions)) / n_actions
# Run Monte Carlo Policy Evaluation
n_episodes = 1000
value_function = monte_carlo_policy_evaluation(policy, n_states, n_episodes, step)
print("Value Function:", value_function)
TD learning policy的伪代码
α
代表学习律,
γ
代表未来权重的折扣因子
\alpha代表学习律,\gamma代表未来权重的折扣因子
α代表学习律,γ代表未来权重的折扣因子
TD learning
Algorithm: TD(0) Policy Evaluation
- 初始化值函数 V(s) 对于所有的状态 s,通常将其设置为 0
- 初始化策略 pi,确定每个状态采取的动作概率
- 选择一个折扣因子 gamma
- 对于每一次迭代:
- a. 初始化状态 s
- b. 当 s 不是终止状态时:
- i. 采取由策略 pi 选择的动作 a
- ii. 从环境中观察到下一个状态 s’ 和奖励 r
- iii. 更新值函数 V(s) = V(s) + alpha * (r + gamma * V(s’) - V(s))
- iv. 更新状态 s = s’
import numpy as np
def step(state, action):
next_state = min(max(state + action, 0), 20)
reward = -abs(next_state - 10)
return next_state, reward
n_states = 21
n_actions = 3
actions = np.array([-1, 0, 1])
policy = np.ones((n_states, n_actions)) / n_actions
V = np.zeros(n_states)
alpha = 0.1
gamma = 0.9
n_episodes = 50000
for episode in range(n_episodes):
state = np.random.randint(0, n_states)
while state != n_states - 1:
action = np.random.choice(actions, p=policy[state, :])
next_state, reward = step(state, action)
td_error = reward + gamma * V[next_state] - V[state]
V[state] += alpha * td_error
state = next_state
print("Value Function:")
print(V)
根据GPT4回答,TD相对于MC的好处
TD(Temporal Difference)学习的确将MC(Monte Carlo)中的G(t)替换为r + gamma * V(s’),这是因为TD学习结合了MC方法和动态规划(DP)的优点。TD学习使用了基于自举(Bootstrapping)的方法,即用当前估计的值函数来更新值函数,这样可以在不知道完整轨迹的情况下进行值函数更新。
相对于MC方法,TD学习具有以下优点:
1.在线学习和实时更新:与MC方法需要等待整个轨迹完>成才能进行值函数更新不同,TD学习可以在线进行,即在每个时间步骤之后立即更新值函数。这使得TD学习更适合实时决策场景。
2.更快的收敛:由于TD学习使用了自举方法,它通常能够更快地收敛到真实值函数,特别是在遇到较长轨迹的情况下。
3.较小的方差:TD学习通常具有较小的方差,因为它不依赖于完整轨迹的返回值,而是使用当前估计的值函数作为更新基础。这使得TD学习的更新通常更稳定。
4.对不完整轨迹的适应性:在某些情况下,观察到的轨迹可能不完整。TD学习可以很好地处理这种情况,因为它不需要完整的轨迹来进行更新。
总的来说,TD学习相对于MC方法具有在线学习、实时更新、更快的收敛速度、较小的方差和对不完整轨迹的适应性等优点。
3.3 bias/variance trade-off
TD的缺点是有偏的估计




import numpy as np
# 定义环境参数
n_states = 5
actions = [0, 1] # 0:不开车, 1:开车
terminal_state = n_states - 1
gamma = 0.9
# 定义策略
policy = np.zeros((n_states, len(actions)))
policy[:, 0] = 1
policy[-1, 1] = 1
# 定义状态转移和奖励函数
def step(state, action):
if action == 1:
next_state = min(state + 1, terminal_state)
reward = -1
else:
next_state = state
reward = -1.5
return next_state, reward
# 执行 Batch Monte Carlo 策略评估
n_episodes = 10000
V = np.zeros(n_states)
returns = [[] for _ in range(n_states)]
for episode in range(n_episodes):
state = 0
episode_trajectory = []
while state != terminal_state:
action = np.random.choice(actions, p=policy[state, :])
next_state, reward = step(state, action)
episode_trajectory.append((state, reward))
state = next_state
G = 0
for t in range(len(episode_trajectory) - 1, -1, -1):
state, reward = episode_trajectory[t]
G = gamma * G + reward
returns[state].append(G)
# 更新状态值函数
for state in range(n_states):
if len(returns[state]) > 0:
V[state] = np.mean(returns[state])
print("Value function:", V)
batch TD learning的policy evaluation的代码
import numpy as np
# 定义环境参数
n_states = 5
n_actions = 2
terminal_state = n_states - 1
gamma = 0.9
n_episodes = 10000
alpha = 0.1
# 定义策略
policy = np.ones((n_states, n_actions)) / n_actions
# 定义状态转换和奖励函数
def step(state, action):
if action == 0: # left
next_state = max(state - 1, 0)
elif action == 1: # right
next_state = min(state + 1, n_states - 1)
reward = -1 if state != terminal_state else 0
return next_state, reward
# 初始化值函数
V = np.zeros(n_states)
# 存储每个状态的所有TD误差
td_errors = [[] for _ in range(n_states)]
for _ in range(n_episodes):
state = 0
episode_trajectory = []
while state != terminal_state:
action = np.random.choice(n_actions, p=policy[state, :])
next_state, reward = step(state, action)
episode_trajectory.append((state, action, reward))
state = next_state
# 计算每个状态的TD误差并将其添加到相应的列表中
for t, (state, action, reward) in enumerate(episode_trajectory[:-1]):
next_state = episode_trajectory[t + 1][0]
td_error = reward + gamma * V[next_state] - V[state]
td_errors[state].append(td_error)
# 使用收集到的TD误差计算每个状态的平均值并更新值函数
for state in range(n_states):
if len(td_errors[state]) > 0:
V[state] += alpha * np.mean(td_errors[state])
print("Value function:", V)
batch MC和普通MC的区别,在跑完了所有的episode以后再进行V(state)的更新
# 更新状态值函数
for state in range(n_states):
if len(returns[state]) > 0:
V[state] = np.mean(returns[state])
那么估计必然会有跑一些episode以后再更新V(state)的策略
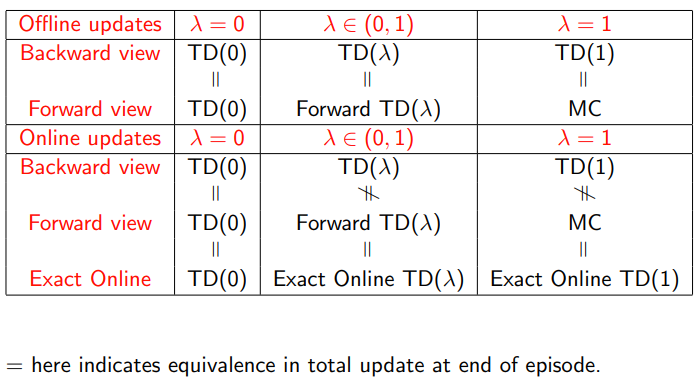
3.4 unified view
- mc backup
V ( S t ) ← V ( S t ) + α ( G t − V ( S t ) ) V(S_t)\leftarrow V(S_t)+\alpha(G_t-V(S_t)) V(St)←V(St)+α(Gt−V(St))

- TD
V ( S t ) ← V ( S t ) + α ( R t + 1 + γ V ( S t + 1 ) − V ( S t ) ) V(S_t) \leftarrow V(S_t)+\alpha (R_{t+1}+\gamma V(S_{t+1}) -V(S_t)) V(St)←V(St)+α(Rt+1+γV(St+1)−V(St))
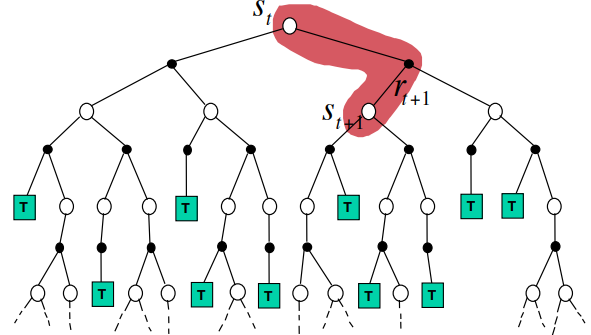
- 动态规划
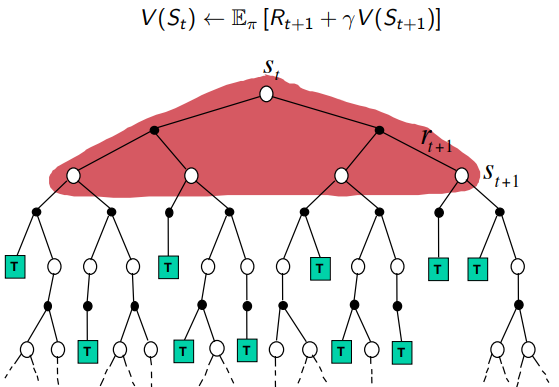
- bootstrapping and sampling

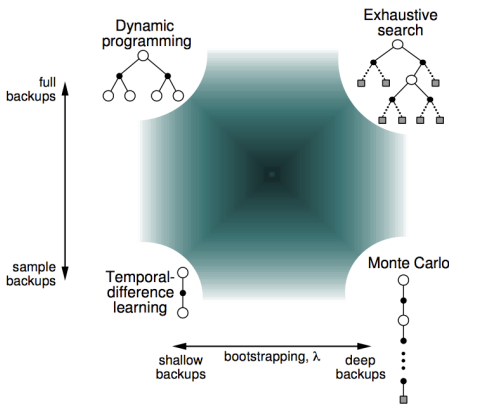
- 比较各种算法
4 TD( λ \lambda λ)
4.1 n step prediction
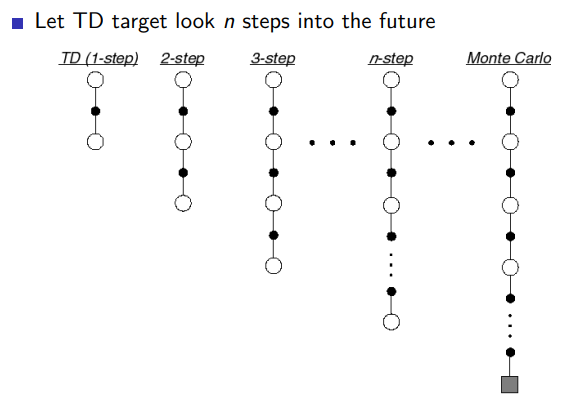

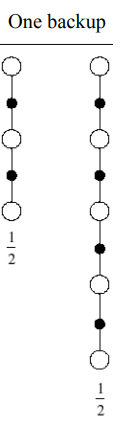
4.2 averaging n-step returns

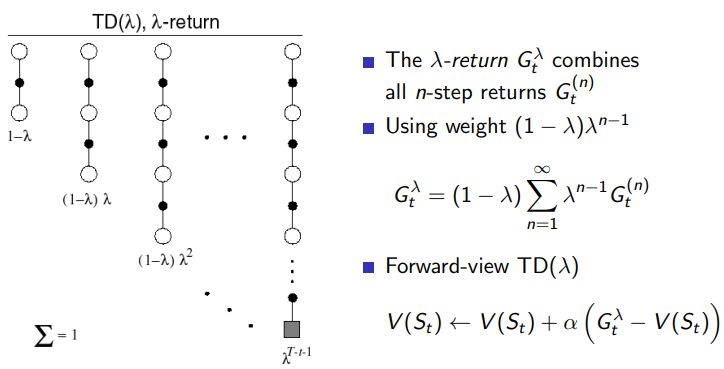
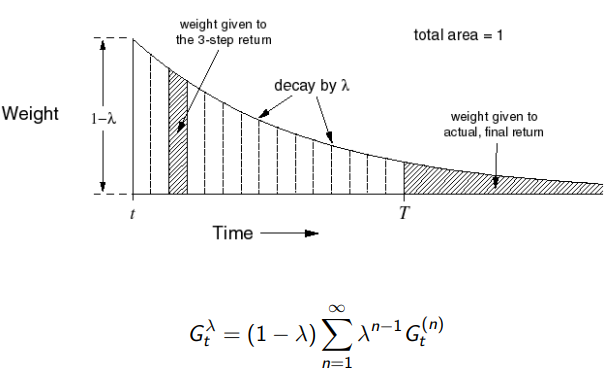
4.3 λ \lambda λreturn
希望后面的结果产生的影响更小,采用
λ
\lambda
λreturn
4.4 forward view td
forward view weighting function
G
t
(
n
)
=
R
t
+
1
+
γ
R
t
+
2
+
.
.
.
+
γ
n
−
1
R
t
+
n
+
γ
n
V
(
S
t
+
n
)
G
t
λ
=
(
1
−
λ
)
∑
n
=
1
∞
λ
n
−
1
G
t
(
n
)
\begin{aligned} G_t^{(n)} & = R_{t+1}+\gamma R_{t+2}+...+\gamma^{n-1} R_{t+n} + \gamma^{n}V(S_{t+n})\\ G_t^{\lambda} &=(1-\lambda)\sum_{n=1}^{\infin}\lambda^{n-1}G_t^{(n)} \\ \end{aligned}
Gt(n)Gtλ=Rt+1+γRt+2+...+γn−1Rt+n+γnV(St+n)=(1−λ)n=1∑∞λn−1Gt(n)
import numpy as np
# 定义环境参数
n_states = 5
n_actions = 2
terminal_state = n_states - 1
gamma = 0.9
n_episodes = 10000
alpha = 0.1
_lambda = 0.9
# 定义策略
policy = np.ones((n_states, n_actions)) / n_actions
# 定义状态转换和奖励函数
def step(state, action):
if action == 0: # left
next_state = max(state - 1, 0)
elif action == 1: # right
next_state = min(state + 1, n_states - 1)
reward = -1 if state != terminal_state else 0
return next_state, reward
# 初始化值函数
V = np.zeros(n_states)
for _ in range(n_episodes):
state = 0
episode_trajectory = []
# 生成情节
while state != terminal_state:
action = np.random.choice(n_actions, p=policy[state, :])
next_state, reward = step(state, action)
episode_trajectory.append((state, reward))
state = next_state
T = len(episode_trajectory)
eligibility_trace = np.zeros(n_states)
# 对每个时间步执行Forward View TD(λ)更新
for t in range(T):
current_state, reward = episode_trajectory[t]
eligibility_trace[current_state] += 1
G_lambda = 0
for k in range(t, T):
state_k = episode_trajectory[k][0]
G_lambda += gamma ** (k - t) * reward * eligibility_trace[state_k]
eligibility_trace[state_k] *= gamma * _lambda
V[current_state] += alpha * (G_lambda - V[current_state])
print("Value function:", V)
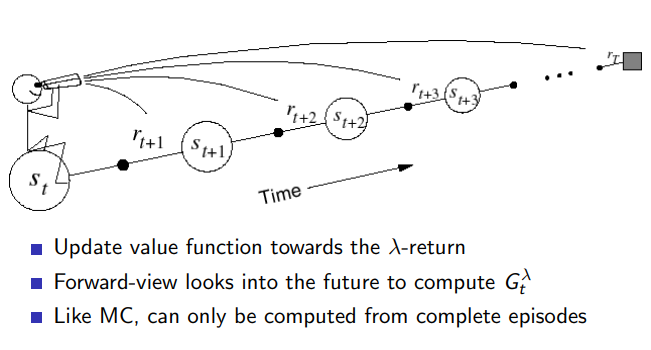
4.5 backward view TD

4.5.1 Eligibility traces
E
0
(
s
)
=
0
E
t
(
s
)
=
γ
λ
E
t
−
1
(
s
)
+
1
(
s
t
=
s
)
\begin{aligned} E_0(s)&=0\\ E_t(s)&=\gamma \lambda E_{t-1}(s)+1(s_t=s) \end{aligned}
E0(s)Et(s)=0=γλEt−1(s)+1(st=s)
Eligibility traces的好处是结合了MC和TD的优点,
# TD(0) 算法: no eligibility traces
V = np.zeros(n_states)
for episode in range(n_episodes):
state = 0
while state != n_states - 1:
next_state, reward = step(state)
V[state] += alpha * (reward + gamma * V[next_state] - V[state])
state = next_state
# TD(λ)算法
for _ in range(n_episodes):
state = 2 # 初始状态
eligibility_trace = np.zeros(n_states)
while state not in terminal_states:
action = np.random.choice(n_actions, p=policy[state, :])
next_state, reward = step(state, action)
eligibility_trace[state] = eligibility_trace[state] * (gamma * _lambda) + 1
delta = reward + gamma * V[next_state] - V[state]
V += alpha * delta * eligibility_trace
eligibility_trace *= gamma * _lambda
state = next_state
Eligibility traces的作用
- 累积效果:通过在每个时间步骤将eligibility trace中的对应状态增加1,我们确保了智能体在同一回合中多次访问同一个状态时,该状态的eligibility trace会累积起来。
- 衰减效果:通过乘以γ * λ因子,我们在每个时间步骤中都对eligibility trace进行衰减。这意味着距离当前状态越远的状态对更新的贡献会越小。
在代码中,我们首先对eligibility trace进行衰减,然后再根据当前状态增加1。这样做的原因是我们想要在算法中引入时间差异的信息,即较早出现的状态在更新中的贡献应该较小。因此,当智能体从状态s到达状态s’时,我们首先对eligibility trace[s]进行衰减,然后再将其值增加1。
通过这种方式,eligibility trace会在每个时间步骤中平衡累积和衰减效果,从而使TD(λ)算法能够利用距离当前状态不同距离的信息来更有效地进行值函数更新。
4.5.2 向后backward的代码
公式
δ
t
=
R
t
+
1
+
γ
V
(
S
t
+
1
)
−
V
(
S
t
)
\begin{aligned} \delta_t &=R_{t+1}+\gamma V(S_{t+1})-V(S_t) \end{aligned}
δt=Rt+1+γV(St+1)−V(St)
import numpy as np
n_states = 5
n_actions = 2
terminal_states = [0, n_states - 1]
# 转移函数
def step(state, action):
if state in terminal_states:
return state, 0
if action == 0: # 左
next_state = max(0, state - 1)
elif action == 1: # 右
next_state = min(n_states - 1, state + 1)
reward = 0 if next_state != n_states - 1 else 1
return next_state, reward
policy = np.ones((n_states, n_actions)) / n_actions
V = np.zeros(n_states)
n_episodes = 5000
alpha = 0.1
gamma = 0.99
_lambda = 0.9
for _ in range(n_episodes):
state = 2 # 初始状态
eligibility_trace = np.zeros(n_states)
while state not in terminal_states:
action = np.random.choice(n_actions, p=policy[state, :])
next_state, reward = step(state, action)
eligibility_trace[state] = eligibility_trace[state] * (gamma * _lambda) + 1
delta = reward + gamma * V[next_state] - V[state]
V += alpha * delta * eligibility_trace
eligibility_trace *= gamma * _lambda
state = next_state
print("Estimated state values:")
print(V)
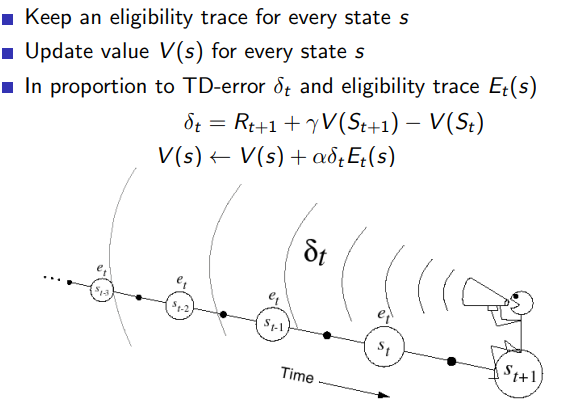
4.5.3 向前视角和向后视角的区别
向前视角 (Forward View) TD:
向前视角 TD 侧重于观察未来的奖励和状态值。它是基于 n 步 TD 预测的概念,即根据过去 n 个时间步长的奖励和状态值来更新当前状态的值。因此,它需要未来 n 步的信息来进行更新。向前视角 TD 的主要问题是它需要在实际应用中等待 n 步,这可能导致较慢的学习速度。
向后视角 (Backward View) TD:
向后视角 TD 试图通过引入 Eligibility Traces 来解决向前视角 TD 的问题。Eligibility Traces 能够追踪过去状态的访问频率以及它们对当前值函数更新的贡献。向后视角 TD 不需要等待未来 n 步,而是在每个时间步立即更新值函数,这使得它在在线学习中更有效。
联系:
尽管向前视角和向后视角 TD 在实现上有所不同,但它们在理论上是等价的。换句话说,在完整的序列上,它们会收敛到相同的值函数估计。事实上,向后视角 TD 可以被视为向前视角 TD 的一种有效实现。
总之,向前视角和向后视角 TD 都是强化学习中估计值函数的方法,但它们的计算方法和实现方式有所不同。向前视角关注未来的奖励和状态值,而向后视角通过引入 Eligibility Traces 来追踪过去状态的访问频率和它们对当前值函数更新的贡献。虽然它们在实现上有所不同,但在理论上它们是等价的。
4.5.4 TD(0)和TD( λ \lambda λ)

4.5.5 MC和TD( λ \lambda λ)

4.6 MC 和TD(1)
E
0
(
s
)
=
0
E
t
(
s
)
=
γ
λ
E
t
−
1
(
s
)
+
1
(
s
t
=
s
)
\begin{aligned} E_0(s)&=0\\ E_t(s)&=\gamma \lambda E_{t-1}(s)+1(s_t=s) \end{aligned}
E0(s)Et(s)=0=γλEt−1(s)+1(st=s)
λ
\lambda
λ





4.7 offline equivalence of forward and backward TD






![[chapter 31][PyTorch][Early Stop Dropout]](https://img-blog.csdnimg.cn/89f222fa4a464e73945433b21ac9d58e.png)