在学习完我们的树形结构之后我们再来使用树形结构的思想构建一个堆。使用堆可以对我们的数据进行排序，并且堆排序的效率要远优于我们之前学习过的冒泡排序。下面我们来逐步实现堆这个数据结构。

  在构建堆之前我们需要先介绍以下我们树形结构构建的两种形式：顺序存储和链式存储。顺序存储的形式也就是使用类似于数组的形式进行数据的存储。针对于树形结构的特点我们可以很容易的发现每一个父节点和孩子节点之间都有一定的关系 parent=(child-1)/2 或者使用儿子节点进行表示：child=parent*2+1表示左孩子，child=parent*2+1+1表示右孩子，测试效果如下：

   我们就可以使用上面的特点在数组当中将各节点当中的数据存储进去。

  我们可以根据上面的父节点和孩子节点之间的相互转换进行指定数据的存储。 但是我们会发现使用顺序存储的形式存储树型结构只适合存储满二叉树。否则就会出现大量的空白造成存储空间的浪费，例如：

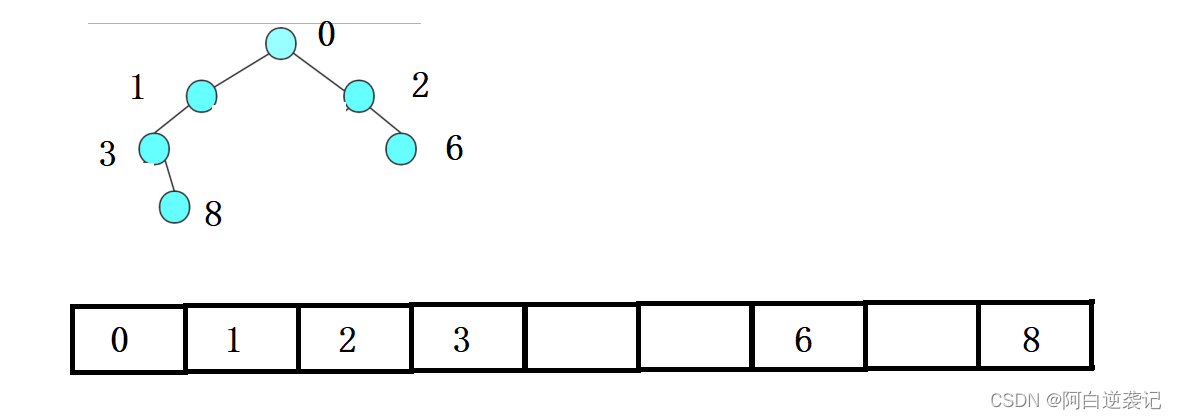  但是对于数据的排序我们使用顺序存储的形式是最合适的，我们只需要构建一个对即可，并且我们构建的堆在定义上是满堆状态。因此我们在本次博客当中主要使用顺序表进行构建堆。（构建链式的二叉树我们将会在下一次博客当中进行详细的讲解。）

  那么我们闲话少说，直接来到我们对于堆的介绍。

  堆有两种形似：大堆和小堆。大堆的定义是：我们父节点当中的数据全部都大于子节点当中的数据。所以我们堆顶的数据是所有要排序的数据当中最大的元素。

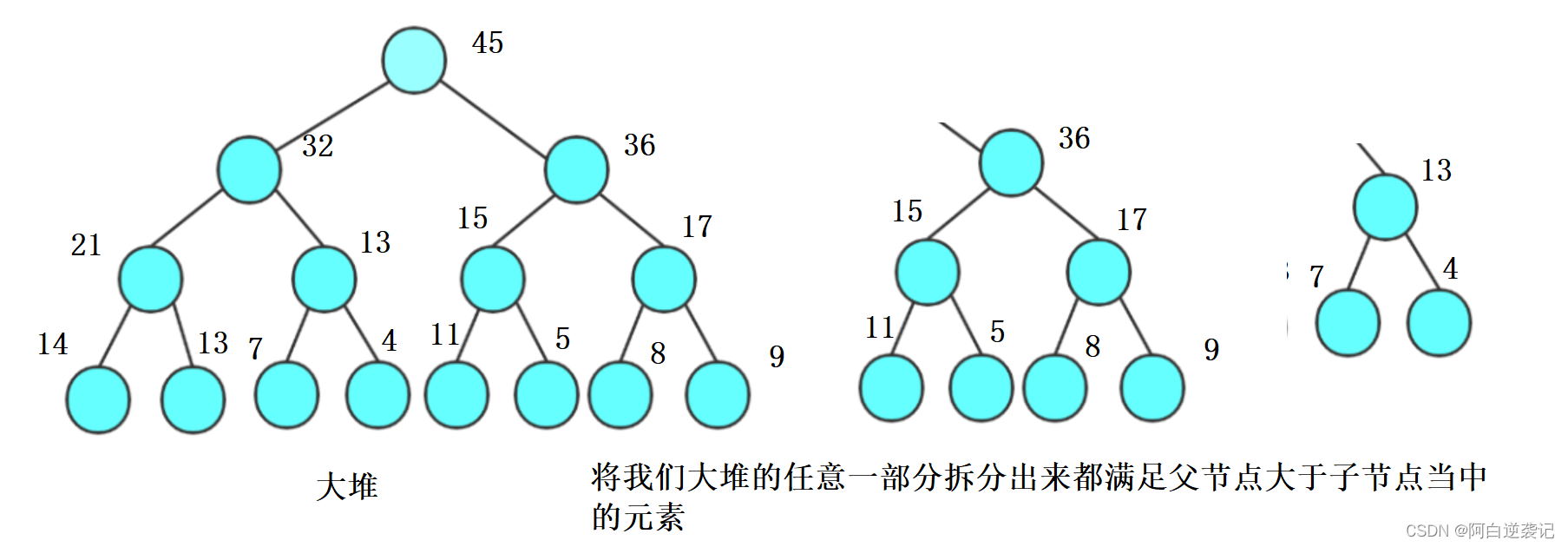   另一种是小堆，和我们的大堆进行类比我们可以猜出小堆的概念是：我们任意一个父节点当中的数据都小于子节点。我们小堆堆当中的元素是我们所有数据当中最小的那个。

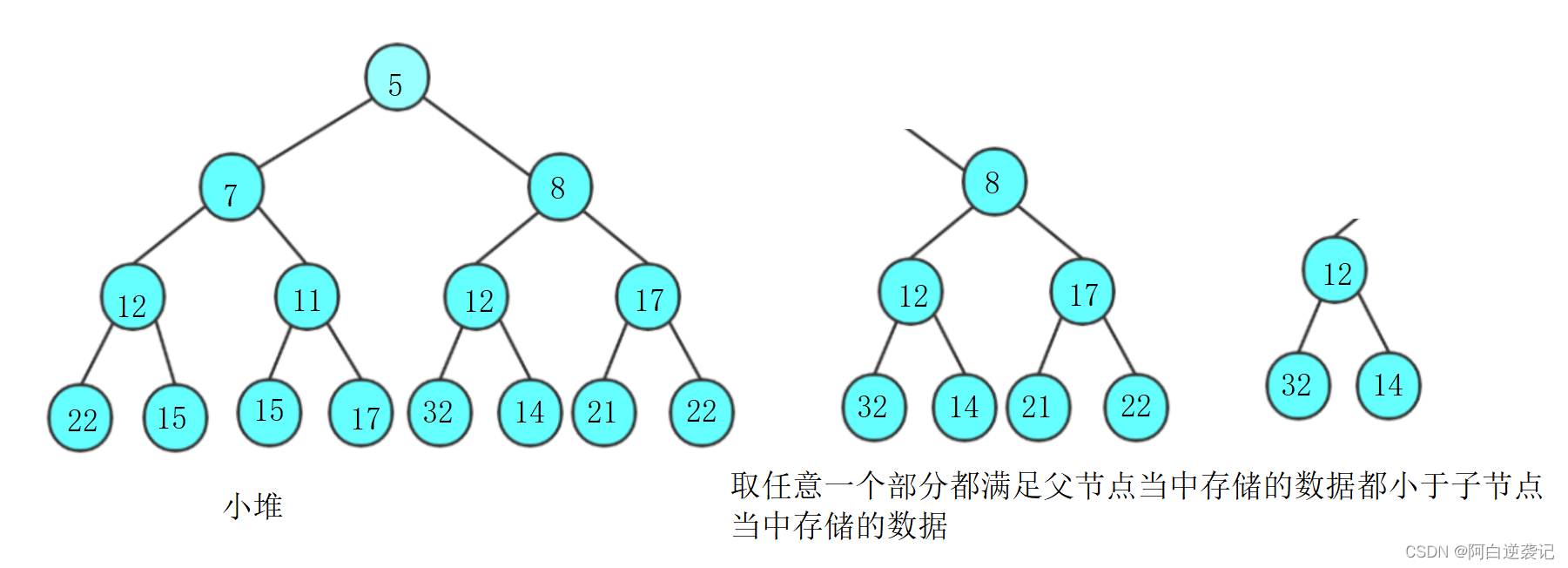  我们可以根据上面的思路使用大堆每次选出数据当中最大的元素使得数组有序。接下来正式开始堆代码的编写。

  由于我们使用的是顺序存储的形式构建的树形结构，（在实际存储的结构形式还是顺序表）所以我们可以先构建一个顺序表之后在进行相应的修改即可。所示的代码如下：

  之后构建一个初始化顺序表的函数：

   该部分代码和我们之前一直使用的顺序表的构建和初始化完全相同，在此就不做过多的解释了。详情请回顾顺序表的博客内容。

  在初始化顺序表之后我们就可以书写向堆中输入数据的函数了。

  首先要想向数组当中插入数据那么我们要做的第一步就是检查数组是否已满，如果入组已满我们就需要进行扩容。之后将我们的数据给到数组指定的位置即可。但是我们要想使用堆进行数据的排序就必须保证我们的堆是一个大堆或者小堆。所以我们就需要构建一个向上调整函数进行数据顺序的调整。也就是我们上面的Adjustup函数。 

   我们会发现当我们数组当中只存在一个数据的时候不需要进行调整，那么我们只需要在插入第二个数据的时候进行调整即可。

  我们可以接着进行测试，插入第三个数据：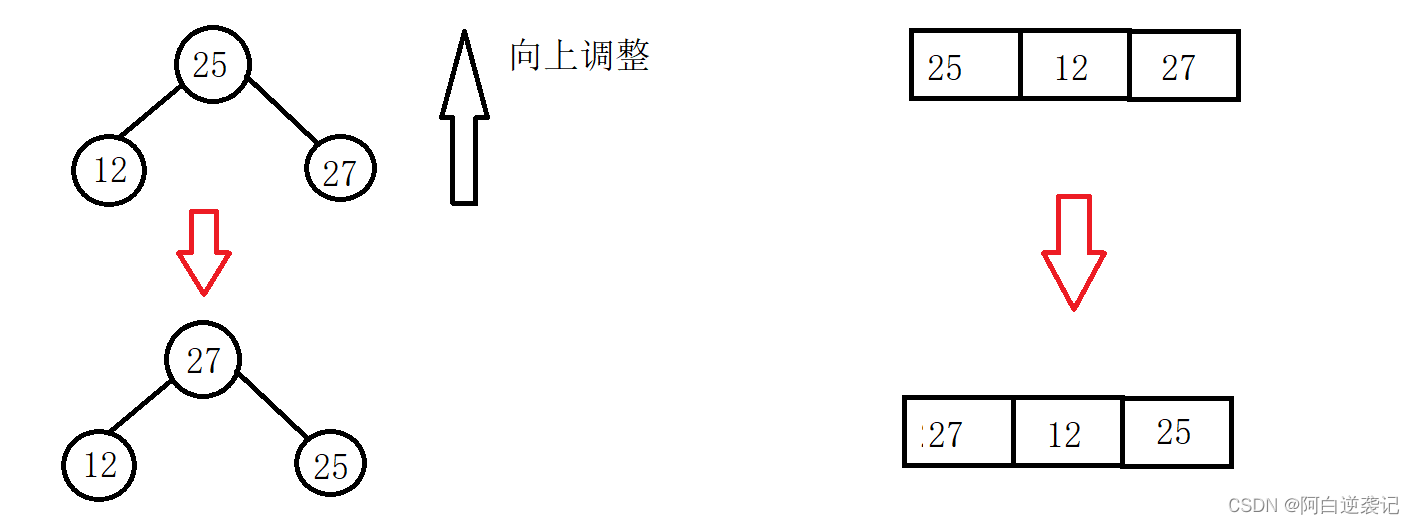

  我们只需要每插入一个数据都对数组进行向上调整，我们构建的堆就一定是大堆。我们先来实现向上调整部分的代码：

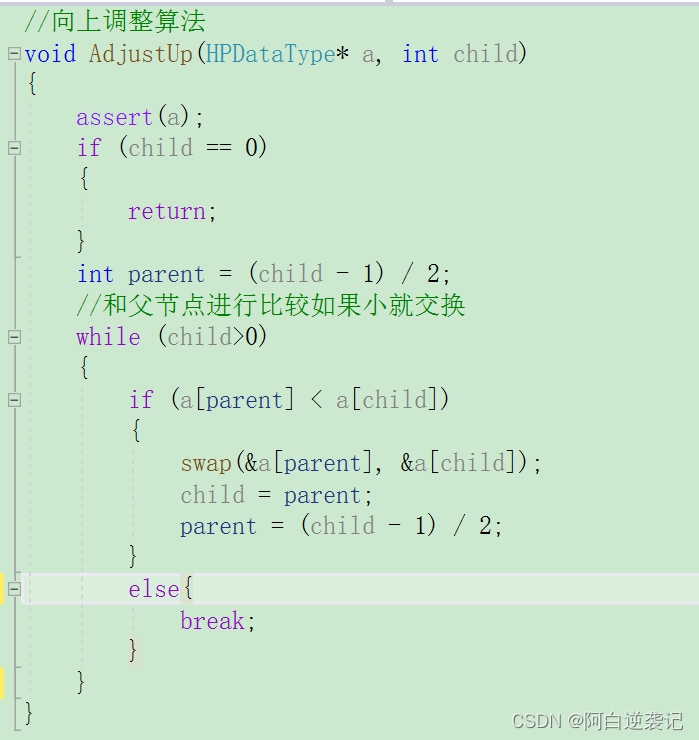   因为我们每一次插入数据都会进行一次向上调整所以我们构建出来的堆一定为大堆。所以我们新插入的数据只需要和我们最近的父节点进行比较如果，子节点当中的数据大于父节点当中的数据就进行交换，否则就不进行交换，当我们不进行交换循环也就结束。当我们和根节点交换之后循环也照常结束。根据上述思路我们可以编写出上述的代码。我们可以测试以下，尝试向数组当中插入一些数据：

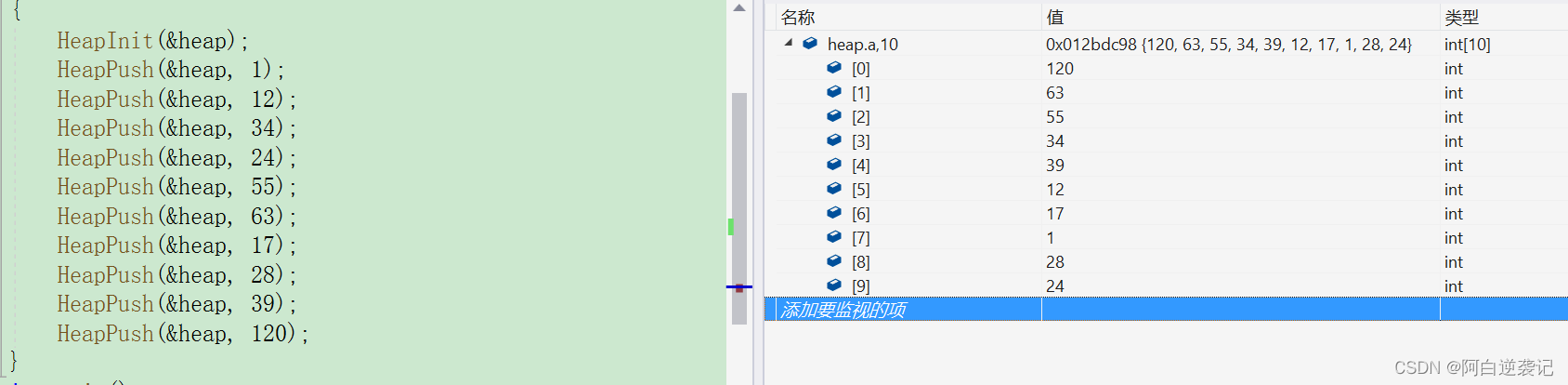   将我们上述的数组中的元素改写成树形结构的形式验证我们数组当中的元素为大堆：

  那么我们向堆中插入数据的函数也就书写完成了。

  既然有插入数据的函数那么一定有删除数据的函数，接下来我们就来构建删除堆中数据的函数。首先我们需要思考的是： 在堆中我们想要删除数据究竟应该删除什么样的数据呢？删除删除什么样的数据才有意义呢？假如我们删除堆低的数据，就像是我们上面创建的堆的表示一样，删除24并没有什么实际意义，24既不是最小的数据也不是最大的数据。我们甚至不知道24在数组当中的地位是怎么样的。但是假如我们想要删除的数据是堆顶的数据的时候，因为我们创建的是一个大堆或者小堆，那么堆顶的数据就是数组当中最大的或者是最小的。我们可以将这个数据删除并返回，之后我们再将我们剩下的数据按照对的形式排列。那么我们就可以继续选择出最大的或者最小的元素了。我们通过代码来了解一下该部分函数的编写：

   和我们所有的删除函数一样，我们进行数据删除操作之前需要先对数组进行判空操作，如果数组当中不存在数据就对数据进行删除。如果我们数组当中只存在一个数据的时候我们就可以直接将我们数组当中的元素删除，不需要再进行元素的调整操作。

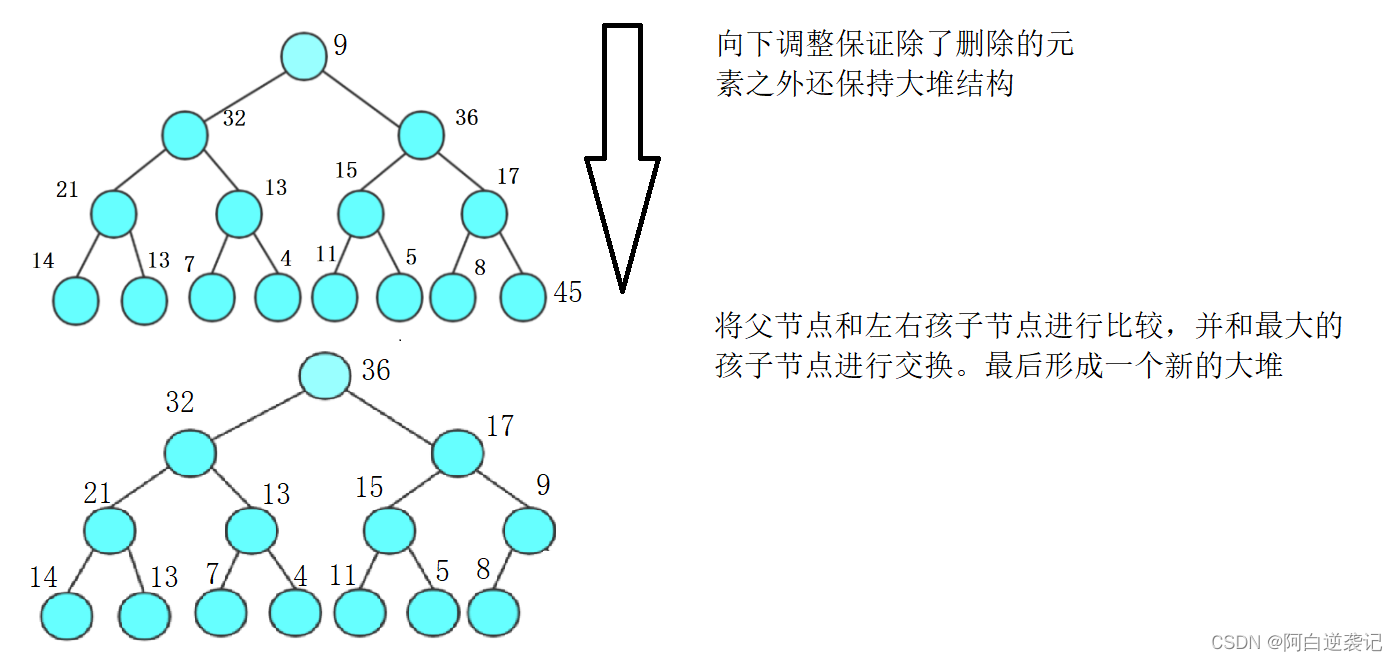  就像是上面我们进行的操作一样，将我们交换之后的堆顶的元素和孩子节点进行比较，并和最大的孩子节点进行交换。最后调整到合适的位置即可。调整之后依旧是一个新的大堆。我们还可以重复上述步骤进行数据的依次选择。最后得到有序的数据列。由于我们上面的的操作是从上到下进行数据的调整的所以我们需要设计一个向下调整函数进行，完成我们上面的操作。代码如下:

 

  之后我们依旧可以对我们编写的代码进行检测：

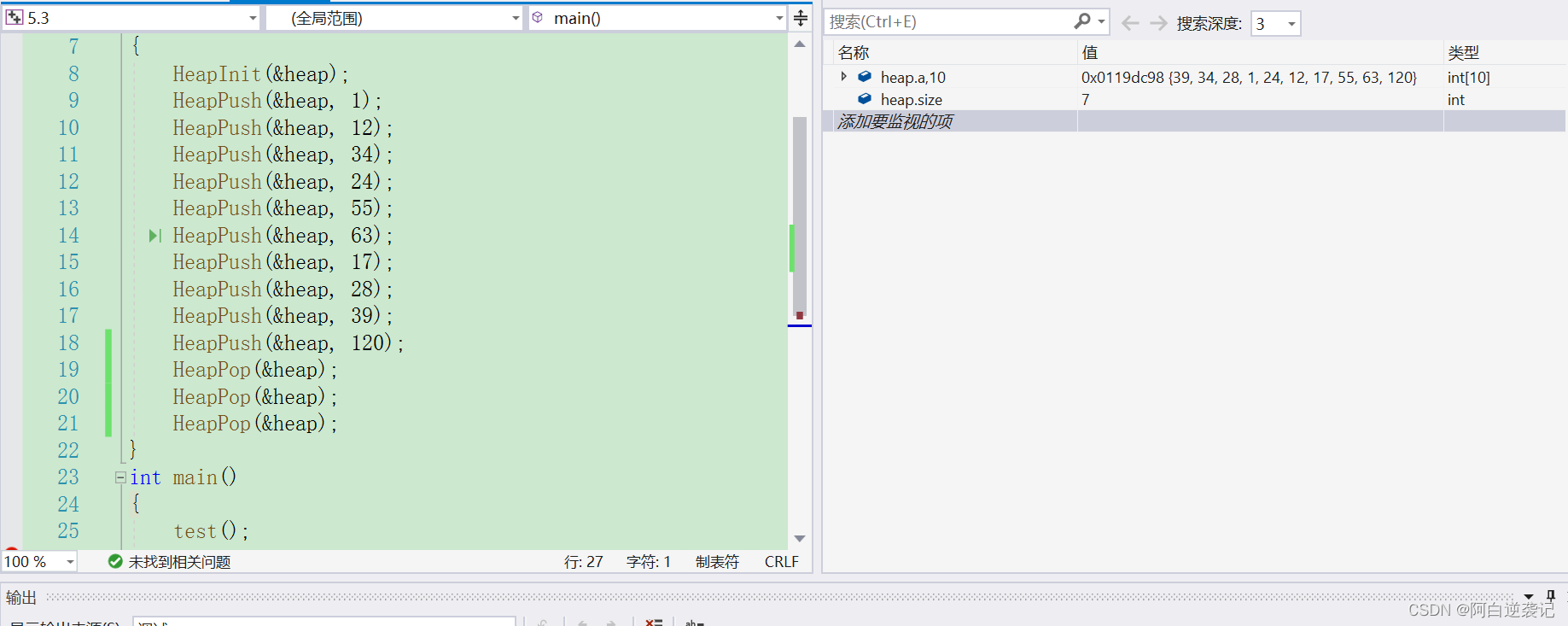   我们通过调试可以发现通过三个删除操作已经将我们最大的三个数据调整到我们数组的最后三个位置上面了，并且我们数组的大小由原本的10变更为7。我们可以将剩余的数据构建一个堆的结构，观察其是否满足大堆的结构特点：

  在构建完我们最主要的插入数据的函数和删除数据的函数之后，只剩下一些便于我们使用的函数了，这些函数的编写内容很简单。

    对堆进行判空的函数：

  我们可以使用这个函数和我们的删除函数相结合，如果堆为空就不进行删除操作。

  返回堆顶元素的函数：

   

  我们可以使用这个函数得到堆顶的最大或者最小的数据，之后再将我们堆顶的元素删除即可。

 判断堆的大小的函数：

堆的销毁函数：

 

  当我们使用完向内存申请的空间之后我们必须将这些空间返回给系统，避免内存泄露的问题。之后我们使用我们上面编写的代码对一些数据进行打印并输出吧！

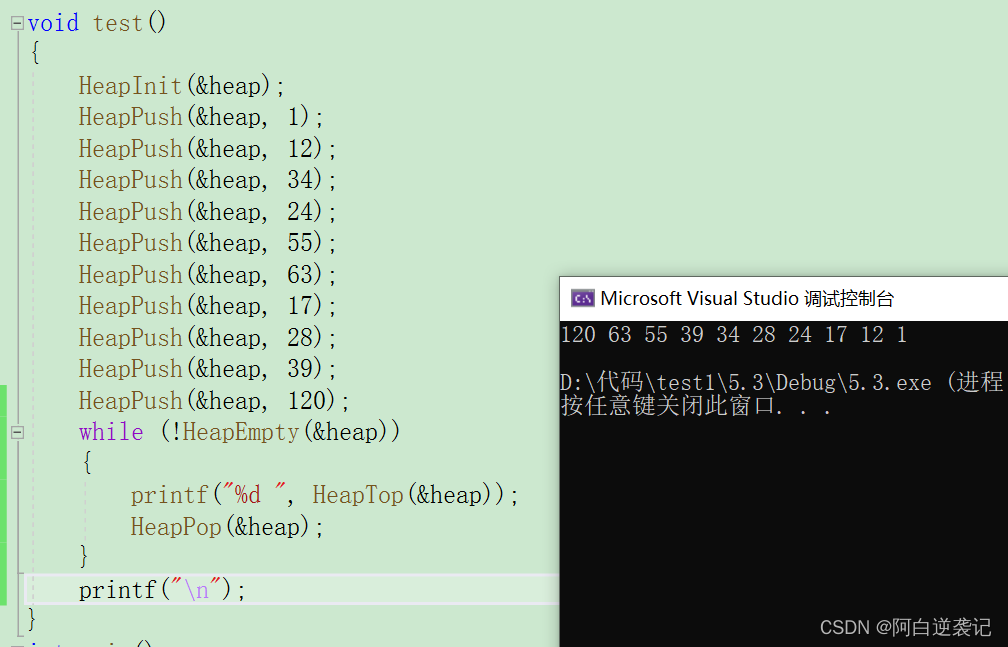   我们会发现我们只需要将我们之前编写的函数结合起来，使用一个简单的for循环便可实现对数据的排序操作了。

  以上我们创建了一个堆（逻辑结构是一颗二叉树）进行数据的排序。在简单的学习完堆的工作原理之后我们将在下一次的博客当中比较堆和冒泡排序函数，方便我们感受堆排序的优点。那么感谢您的观看，祝您天天开心。